Model | LLemma | Compute-Optimal Inference Analysis

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-05

An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models

• url: https://arxiv.org/abs/2408.00724
• pdf: https://arxiv.org/pdf/2408.00724
• html: https://arxiv.org/html/2408.00724v1
• abstract: The optimal training configurations of large language models (LLMs) with respect to model sizes and compute budgets have been extensively studied. But how to optimally configure LLMs during inference has not been explored in sufficient depth. We study compute-optimal inference: designing models and inference strategies that optimally trade off additional inference-time compute for improved performance. As a first step towards understanding and designing compute-optimal inference methods, we assessed the effectiveness and computational efficiency of multiple inference strategies such as Greedy Search, Majority Voting, Best-of-N, Weighted Voting, and their variants on two different Tree Search algorithms, involving different model sizes and computational budgets. We found that a smaller language model with a novel tree search algorithm typically achieves a Pareto-optimal trade-off. These results highlight the potential benefits of deploying smaller models equipped with more sophisticated decoding algorithms in budget-constrained scenarios, e.g., on end-devices, to enhance problem-solving accuracy. For instance, we show that the LLemma-7B model can achieve competitive accuracy to a LLemma-34B model on MATH500 while using 2× less FLOPs. Our findings could potentially apply to any generation task with a well-defined measure of success.

어닐링 혹은 Scaling Law와 관련해서는 Pythia가 주로 사용되는 것 같습니다. 그 외 일부 데이터에 대해 학습시켜 방법을 실험해 효용을 증명하는 논문들은 Math 데이터 및 벤치마크가 많이 활용되는 것 같습니다. 편의상 Prune은 프루닝으로 번역합니다.

Inference Cost Caling raw and llema

[Emperical한 증명 관련 색인마킹]

TL;DR

1. LM의 성능과 계산량을 최적화하는 연구를 통해 인퍼런스 비용 대비 최대 성능을 달성합니다. (e.g., 오류율 최소화)
2. 다양한 인퍼런스 전략(e.g., 그리디 검색, 빔 서치 등)과 알고리즘(i.e., REBASE)의 효율성을 비교하고, 특히 수학 문제에 최적화된 모델을 평가합니다.
3. MATH와 GSM8K 데이터셋을 사용하여 인퍼런스 계산 스케일링과 REBASE 방법의 성능을 실험적으로 평가합니다.
4. 비용 대비 모델의 성능을 비교하고, REBASE가 기존 트리 검색 기법에 비해 우수한 성능을 보임을 확인합니다.
5. 계산 최적화 인퍼런스를 통해 작은 모델을 사용할 때 경쟁력 있는 정확도를 달성하며, 복잡한 수학 문제에 대한 더 깊은 연구를 제안합니다.

1. 서론

최근의 연구들은 대규모 뉴럴 네트워크가 언어 모델링, 이미지 모델링, 비디오 모델링, 보상 모델링, 보드 게임 등 다양한 분야에서 어떻게 확장되고 있는지를 보여줍니다. 이들 연구는 모델의 크기와 훈련 계산량이 모델 성능에 미치는 영향을 규명했습니다.

그러나 모델 훈련 후 인퍼런스 단계에서 계산량을 조정하는 것이 모델 성능에 어떤 영향을 미치는지에 대한 지식은 제한적입니다.

이 논문에서는 다양한 인퍼런스 알고리즘과 대규모 언어모델의 구성을 심도 있게 분석하고, 효율적인 모델 크기와 인퍼런스 전략을 선택하는 방법을 탐구합니다.

2. 관련 연구

• 대규모 언어모델은 최근 몇 년 동안 크게 발전하여 강력한 인퍼런스 능력을 보여주었습니다. 수학 문제 해결은 언어 모델의 인퍼런스 능력을 측정하는 핵심적인 과제로 남아있습니다.
• 다양한 디코딩 전략이 개발되었으며, 이는 훈련된 모델을 사용하여 시퀀스를 생성하는 데 사용됩니다. 그리디 디코딩, 빔 서치, Monte Carlo Tree Search(MCTS)와 같은 방법들이 소개되었으며, 이들 방법은 비용을 사용하여 성능을 향상시키는 trade-off를 분석하는 것이 필요합니다.
• 과정 보상 모델: 이 모델들은 LLM이 생성한 시퀀스의 중간 단계에 보상을 부여하여 인퍼런스 및 문제 해결 능력을 향상시키며 선택된 해결책의 오류율을 낮추고, 다단계 인퍼런스 과정을 유도하는 데 효과적일 수 있습니다.

이 논문에서는 다양한 인퍼런스 전략과 언어 모델 크기를 조절하면서 비용을 고려하여 최적의 성능을 달성하는 방법을 실험적으로 평가합니다.

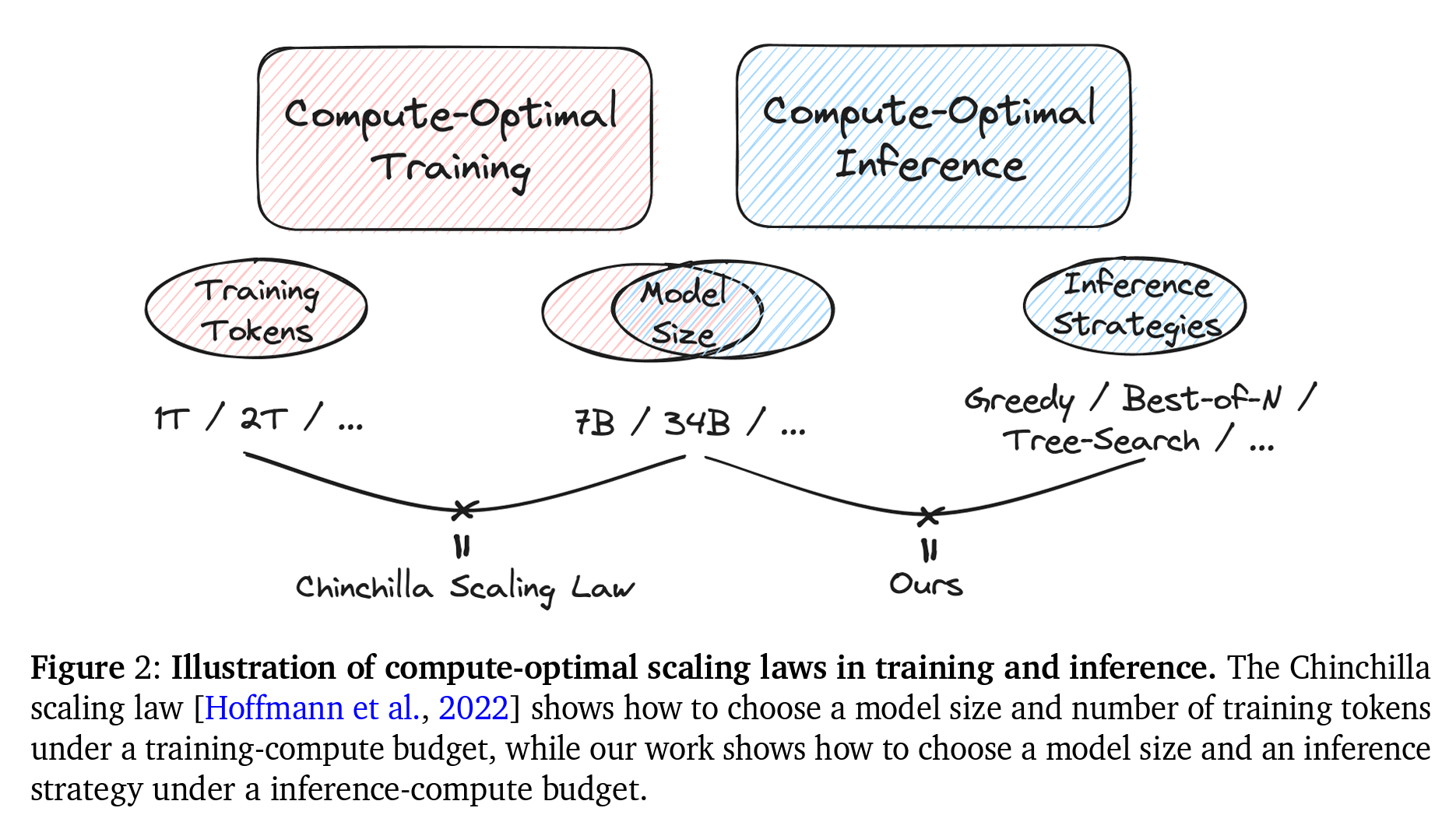
• 인퍼런스 계산 최적화

  모델의 크기와 사용된 토큰의 수를 조절하여 비용 대비 최대의 성능을 달성하도록 합니다. 예를 들어, $FLOPs$의 예산 하에서 최적의 모델 크기를 선택하는 문제는 다음과 같이 수식화할 수 있습니다. ($E$는 오류율을 의미)

  \[\text{minimize } E(\text{model size}, \text{compute budget}) = \text{Error Rate}\]

• 수학적 인퍼런스 벤치마크 활용

  GSM8K 테스트 세트와 MATH500 테스트 세트를 사용하여 언어 모델의 인퍼런스 능력을 평가합니다. 이런 벤치마크를 사용하여 다양한 모델 구성에서의 성능을 분석하고, 특히 수학 문제에 특화된 모델(LLemma)의 성능을 비교합니다.

• REBASE 알고리즘의 도입

  새로운 트리 서치 알고리즘인 REBASE는 노드 품질 기반 보상을 사용하여 트리 탐색의 활용과 프루닝 속성을 제어하며, 충분한 후보 해결책을 위한 보팅 또는 선택을 보장할 수 있습니다. ($\text{quality(node)}$는 노드의 품질을 평가하는 함수, $\text{threshold}$는 프루닝을 결정하는 기준)

  \[\text{REBASE}(\text{node}) = \begin{cases} \text{explore} & \text{if quality(node) > threshold} \\ \text{prune} & \text{otherwise} \end{cases}\]

3 계산 최적화 인퍼런스를 위한 문제 해결

3.1 문제 정의

고정된 FLOPs 예산 하에서 정책 모델의 최적 모델 크기와 효과적인 인퍼런스 전략을 선택하여 성능(즉, 정확도)을 최대화하는 방법을 탐구합니다. 이 문제를 처음으로 정의하고 인퍼런스 시간 스케일링 법칙을 연구함으로써, 기존의 스케일링 법칙 연구와 차별화됩니다.

문제 해결 오류율 $E(N, T; \mathcal{S})$를 모델 파라미터 수 $N$, 생성된 토큰 수 $T$, 인퍼런스 전략 $\mathcal{S}$의 함수로 나타냅니다. 계산 예산 $C$는 다음과 같은 결정적 함수 $FLOPs(N, T; \mathcal{S})$를 기반으로 합니다. ($N_{opt}(C)$와 $T_{opt}(C)$는 계산 예산 $C$에 대한 최적 할당)

정책 모델을 통해 더 많은 토큰을 생성함으로써 고정된 모델의 인퍼런스 계산량(FLOPs)을 조절할 수 있습니다. 예를 들어, 후보 솔루션을 추가로 샘플링하고 보상 모델을 사용하여 순위를 매기는 방식으로 조절할 수 있습니다.

Re-rank 또는 다수결 보팅의 경우 더 많은 토큰을 소비하기 때문에 주로 샘플링 및 트리 검색 접근 방식을 사용했다고 언급합니다.

3.2 인퍼런스 전략

3.2.1 샘플링 기반 방법

다음과 같이 실제로 널리 사용되는 샘플링 기반 인퍼런스 전략을 고려합니다.

• Greedy Search: 이 전략은 각 단계에서 가장 높은 확률의 토큰을 선택하여 한 번에 하나의 토큰을 생성합니다. 계산 효율성은 높으나 다양성 측면에서는 종종 최적이 아닙니다.
• Best-of-N: 이 전략은 여러 솔루션을 샘플링하고 보상 모델에 의해 주어진 최고 점수를 가진 솔루션을 선택합니다.
• Majority Voting: 이 전략에서는 여러 모델 출력을 생성하고, 모든 출력에서 가장 자주 등장하는 답변을 최종 문제의 답으로 결정합니다.
• Weighted Majority Voting: 이 전략은 Majority Voting의 변형으로, 보상 모델에 의해 주어진 점수에 기반한 가중치를 적용해 보팅에 적용합니다.

보다 정교한 인퍼런스 알고리즘(e.g., 트리 검색)을 다루기 전에, 무한한 계산에서 보팅 기반 전략의 점근적 행동에 대한 이론적 결과를 Theorem 1 및 Theorem 2로 제시합니다.

Theorems

Theorem 1 및 Theorem 2의 경우 표준/가중 다수결 보팅의 정확도는 무한한 샘플로 수렴하며, 언어 모델(및 보상 모델)에 의해 모델링된 분포에만 제약이 가해진다는 것을 보이는 것에 중점을 둡니다.

위 이론적 발견은 4.2절에서 확인하는 경험적 결과와도 일치하며, 증명은 Appendix A에서 상세하게 제시됩니다.

사전 정의 및 가정

유한한 어휘 \(\mathcal{V}\)와 그 Kleene closure(스타클리니 클로저) \(\mathcal{V}^*\), 즉 모든 문자열의 집합을 고려합니다.

문제 $x$에 대해, 언어 모델이 이 문제에 대해 답변 $y$를 한다고 할 때, 모델은 \(re\,y\)를 출력하며, \(r \in \mathcal{V}^*\)은 임의의 “reasoning paths”이고 $e \in \mathcal{V}$는 인퍼런스의 끝을 나타내는 특별한 토큰입니다.

답변 문자열은 항상 $L$ 토큰보다 짧다고 가정합니다, 즉 \(\|y\| \leq L\)이며 언어 모델 $\pi$에 대해, \(\pi(v \mid w)\)는 입력(프롬프트) $w$가 주어졌을 때 $v$를 생성할 확률을 나타냅니다.

보상 모델 $\rho$에 대해, $\rho(v)$는 문자열 $v$에 할당된 점수를 나타내며, 지시 함수의 경우 $\mathbb{I}$로 표시합니다.

Theorem 1

데이터셋 \(\mathcal{D} = \{(x_i, y_i)\}_{i=1}^m\)을 고려할 때, $x_i$와 $y_i$는 각각 입력과 참 답변을 나타냅니다. 언어 모델 $\pi$에 대해, \(\text{acc}_{MV}^n(\mathcal{D}; \pi)\)는 $n$개의 샘플을 사용한 다수결 보팅으로 \(\mathcal{D}\)에서의 정확도를 나타냅니다. 위에서 정의한 가정과 표기법을 따를 때, 다음을 갖습니다.

Theorem 2

데이터셋 \(\mathcal{D} = \{(x_i, y_i)\}_{i=1}^m\)을 고려할 때, 언어 모델 $\pi$와 보상 모델 $\rho$에 대해, \(\text{acc}_{WV}^n(\mathcal{D}; \pi, \rho)\)는 $n$개의 샘플을 사용한 가중 다수결 보팅으로 $\mathcal{D}$에서의 정확도를 나타냅니다. 위에서 정의한 가정과 표기법을 따를 때, 다음을 갖습니다.

이 Theorem들은 샘플 수가 증가함에 따라 정확도가 수렴함을 나타내며, 모든 고정된 모델에 대해 사용된 샘플의 성능 향상이 포화될 것임을 보입니다. 즉, 가능한 모든 reasoning paths를 통해 올바른 답변을 생성할 가능성에 의해 결정되며, 결과는 트리 검색 기반 변형과 같이 “good” reasoning paths를 찾기 위한 인퍼런스 알고리즘을 고려하도록 동기를 부여합니다.

더 복잡한 인퍼런스 알고리즘(e.g., 트리 검색)을 다루기 전에, 무한한 계산에서 보팅 기반 전략의 점근적 행동에 대한 이론적 결과를 제시합니다. Theorem 1과 2에서, 표준/가중 다수결 보팅의 정확도가 무한 샘플로 수렴함을 보여줍니다. 정확도의 한계는 언어 모델(및 보상 모델)에 의해 모델링된 분포에만 의존하며, 이 이론적 발견은 4.2절에서 보여진 경험적 결과와도 일치합니다. (Appendix A 참조)

3.2.2 몬테 카를로 트리 검색(MCTS)

MCTS는 전략적 의사결정이 필요한 보드 게임과 같은 도메인에서 효과적임이 입증되었으며, 종종 가치 모델과 함께 사용되어 탐색 단계를 점수 매기고 안내하는 역할을 합니다.

최근에 다른 연구들에서 MCTS를 LLM의 맥락에 적응시켜, 텍스트 생성 과정을 강화하는 방법을 소개했습니다. (Appendix B 참조)

3.2.3 보상 균형 검색(REBASE)

REBASE 트리 검색 방법은 트리 검색의 활용 및 프루닝 속성을 상속받으면서, 추가 계산 없이 보상 모델만을 사용하여 노드의 품질을 평가합니다. 트리의 특정 깊이에서 총 확장 너비를 제한함으로써 효율을 높입니다.

즉, REBASE는 동일 깊이의 노드 간에 보상에 따라 확장 너비를 균형있게 조정할 수 있습니다.

[REBASE 알고리즘 상세]

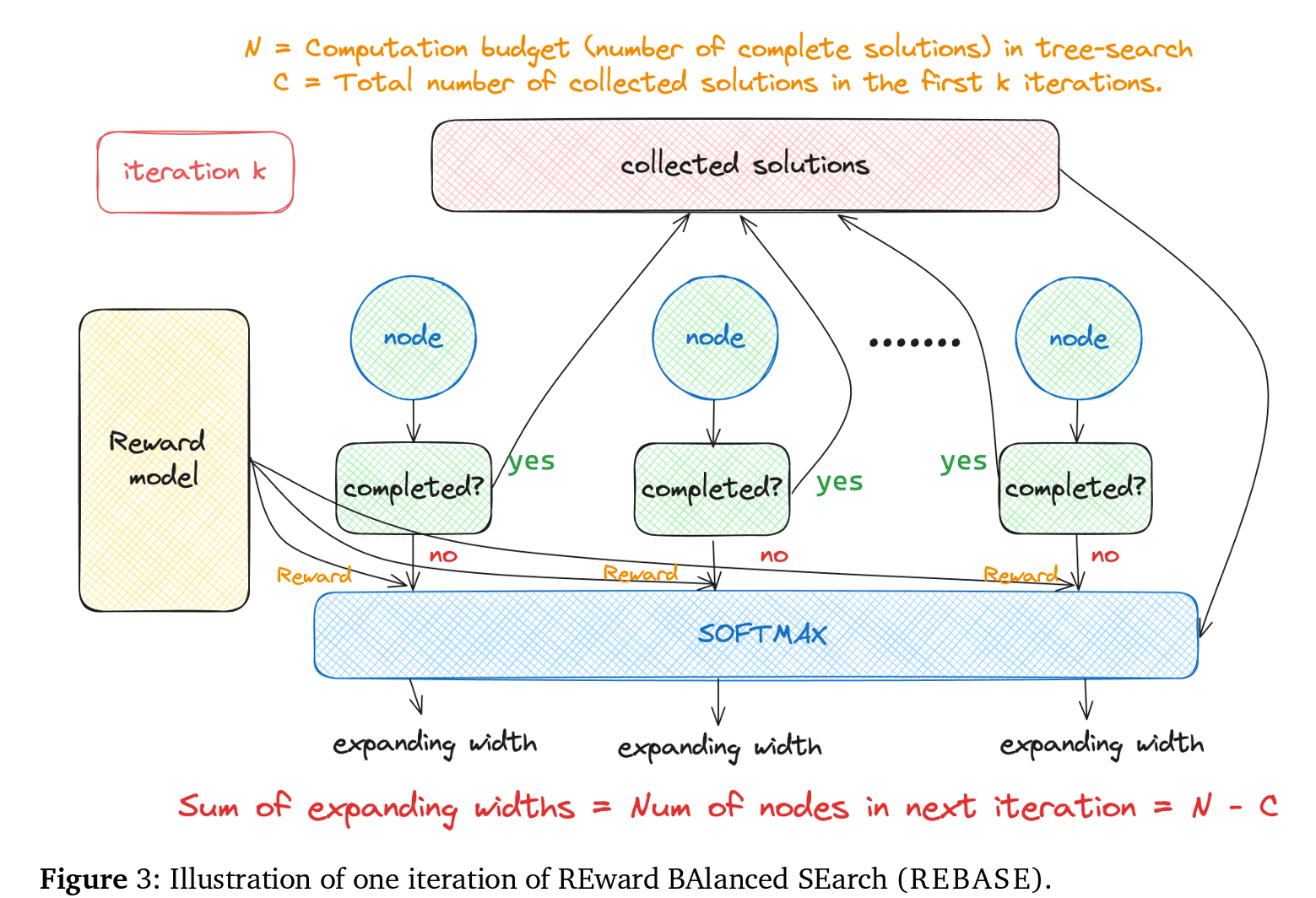
(1) 초기화

주어진 질문 $x$, 균형 온도 $T_b > 0$, 그리고 솔루션 수 $N$에 대해, 질문의 첫 단계에 대해 $N$ 인스턴스를 샘플링하여 검색 트리의 깊이 1의 모든 노드를 생성합니다. 초기화에서 깊이 0의 샘플링 예산 $B_0$을 $N$으로 설정합니다.

(2) 보상 모델링 및 업데이트

$i$-번째 반복에서, 프로세스 보상 모델(PRM)은 깊이 $i$의 모든 노드에 보상을 할당합니다. 그 후, 알고리즘은 깊이 $i$까지의 솔루션이 완료되었는지 검사합니다. $C_i$ 완료된 솔루션이 있다고 가정할 때, 샘플링 예산을 $B_i \leftarrow B_{i-1} - C_i$로 업데이트합니다. 만약 $B_i = 0$이면, 과정이 종료되고 $N$ 솔루션을 얻습니다.

(3) 탐색 균형 및 확장

깊이 $i$의 트리에서 보상 $R(n_j)$을 받은 모든 노드 $n_j$에 대해, $n_j$의 확장 너비를 다음과 같이 계산합니다.

(4) 그런 다음 모든 노드 $n_j$에 대해 $W_j$ 자식을 샘플링하고 다음 반복을 시작합니다.

위와 같은 순서대로 REBASE는 비용을 최소화하면서 효율적으로 높은 품질의 솔루션을 탐색할 수 있다고 주장하며, 기존의 트리 검색 방법들이 대규모의 계산 자원을 필요로 하는 문제를 해결함으로써, 보다 효율적인 인퍼런스가 가능하도록 할 수 있다고 언급합니다.

4. 실험

4.1 실험 설정

• 데이터셋: MATH (Hendrycks et al., 2021a)와 GSM8K (Cobbe et al., 2021b) 두 수학 문제 해결 데이터셋을 사용하여 계산의 스케일링 효과와 REBASE 방법을 조사했습니다. MATH500 부분집합을 테스트 세트로 사용합니다.
• 정책 모델 (생성기): 인퍼런스 계산 스케일링 효과를 연구하기 위해 Pythia 모델을 기반 모델로 선택했습니다. 트리 검색에는 수학 전문 LLemma 모델을 사용했습니다.
• 보상 모델: 모든 실험에서 동일한 LLemma-34B 보상 모델을 사용했으며, 이를 수학 과정 보상 모델링 데이터셋인 Math-Shepherd에 대해 파인튜닝했습니다.
• 인퍼런스 구성: 샘플링 및 트리 검색 방법을 사용하여 여러 샘플을 생성하고 Best-of-N, Majority Voting, Weighted Voting을 통해 답변을 선택했습니다.

4.2 주요 결과: 최적 계산 인퍼런스

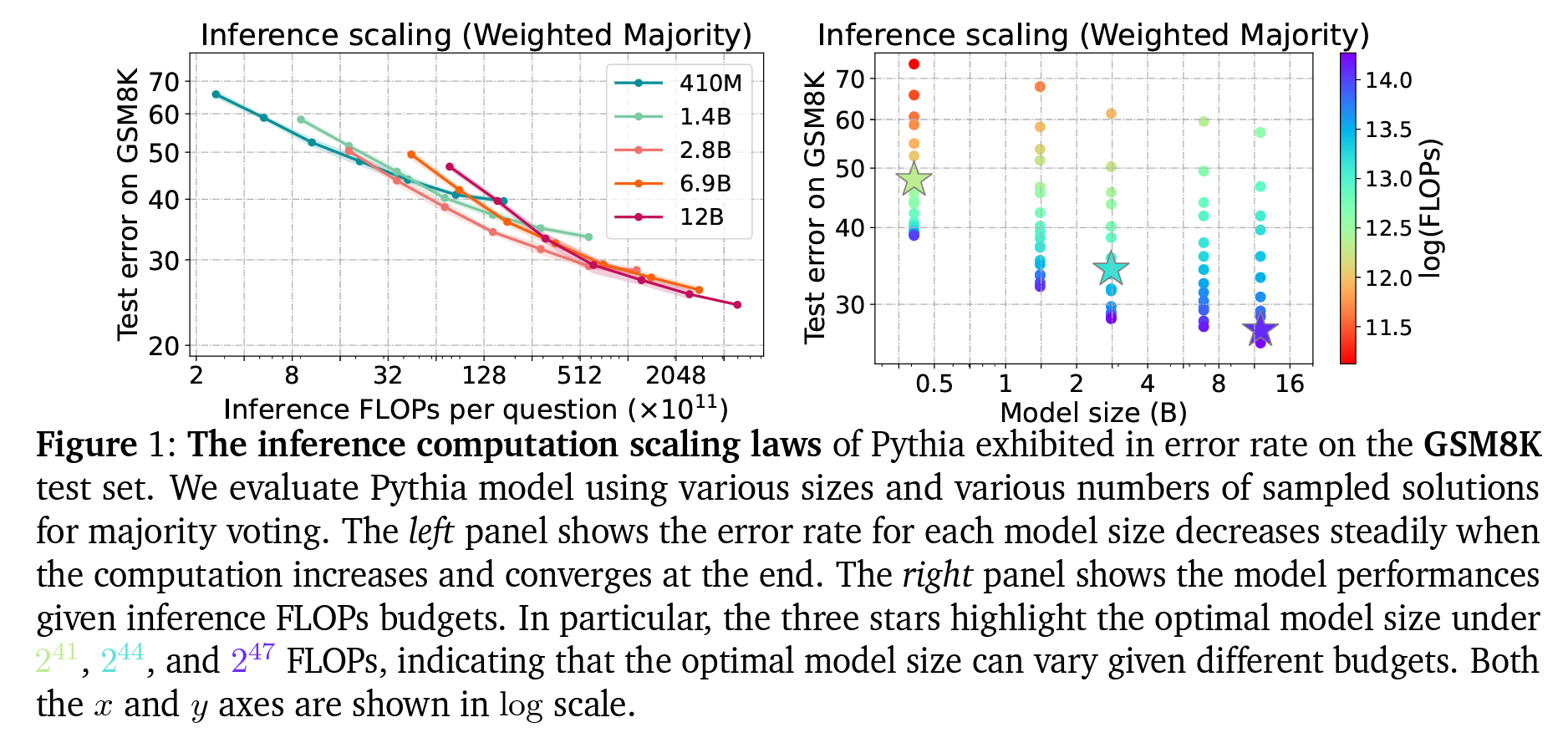
• 계산 스케일링 법칙: 인퍼런스 계산 예산의 스케일링 효과는 Fig. 1에서 보여집니다. 오류율은 먼저 꾸준히 감소하다가 포화 상태에 이릅니다. 작은 모델이 제한된 예산으로 더 많은 샘플을 생성할 수 있으므로 처음에는 이점이 있지만, 더 많은 FLOPs를 사용할 때는 LM이 선호됩니다.
• LLemma-7B 모델 성능: LLemma-7B 모델은 LLemma-34B 모델과 비슷한 정확도를 보이면서 계산 예산을 약 2배 덜 사용합니다. 이는 트레이닝 데이터셋과 모델 패밀리가 같을 때, 작은 모델을 사용하는 훈련과 인퍼런스가 계산 예산 측면에서 더 유리할 수 있음을 시사합니다.

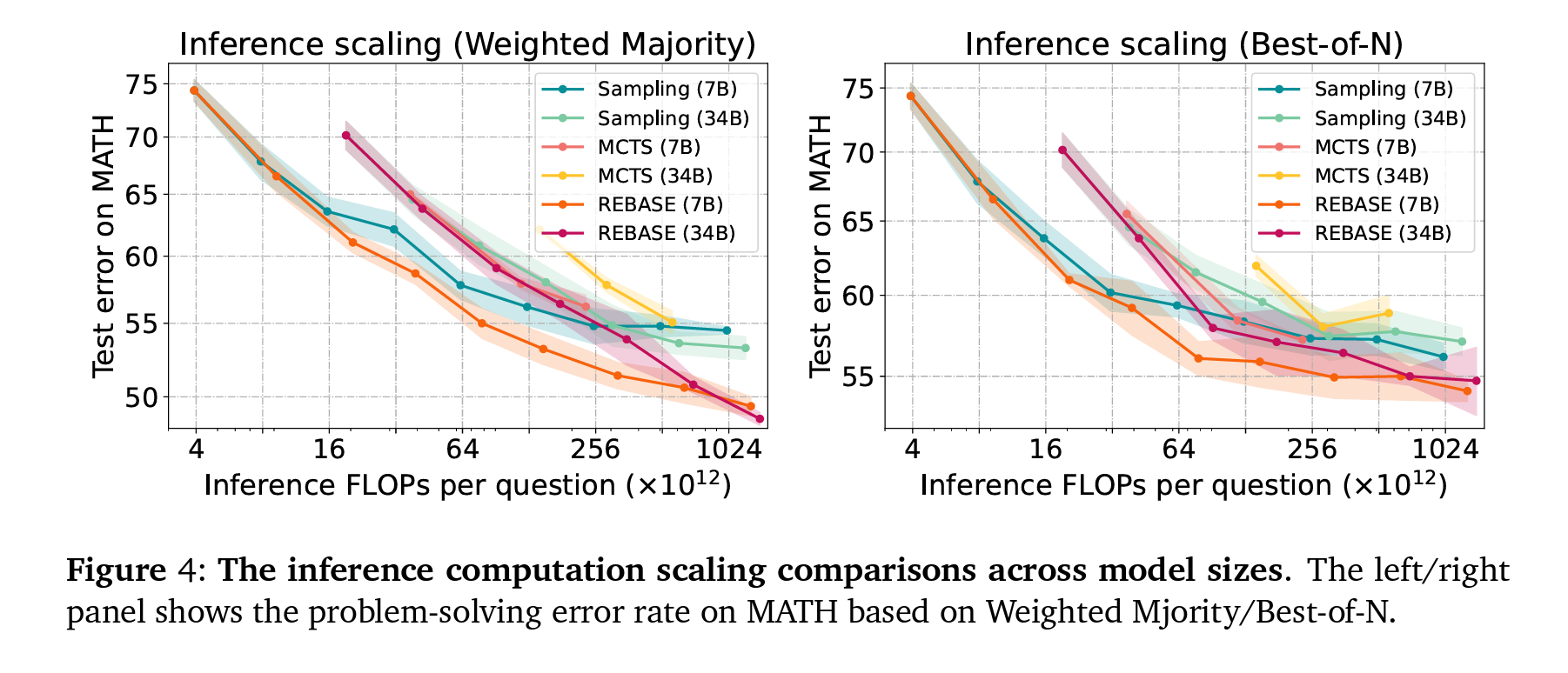
4.3 REBASE와 기타 기준 방법 비교

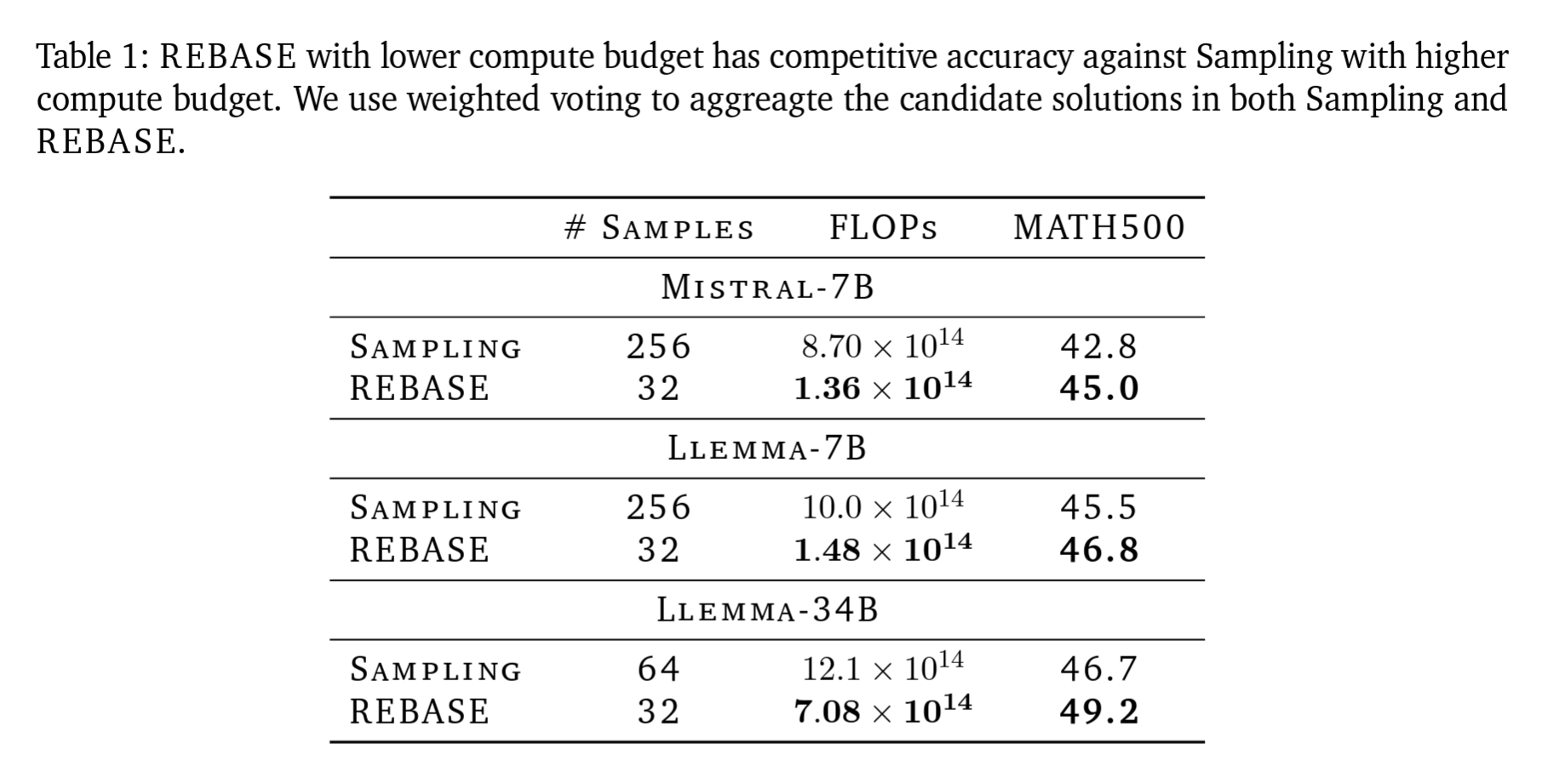
• REBASE는 MCTS를 포함한 기타 샘플링 방법보다 일관되게 더 높은 성능을 보였습니다. REBASE는 샘플링 방법보다 낮은 계산 예산으로 비슷하거나 더 높은 정확도를 달성할 수 있음을 Table 1에서 확인할 수 있습니다.
• 트리 검색의 이점: 특히 더 약한 모델에서 트리 검색 방법이 더 큰 이점을 보였습니다. REBASE는 Mistral-7B, LLemma-7B, LLemma-34B 모델에서 각각 5.3%, 3.3%, 2.6%의 성능 향상을 보입니다.
• REBASE의 성능 포화: REBASE는 샘플링보다 늦게 성능 포화가 발생하며, 더 높은 정확도를 달성하는데, 이는 REBASE가 샘플링보다 진실된 답변을 더 높은 확률로 샘플링할 수 있기 때문이라고 언급합니다.

5. 결론 및 한계점

본 연구에서는 대규모 언어모델의 인퍼런스 성능을 최적화하기 위해 다양한 계산 전략을 실험하고 평가하였습니다. 결과적으로, 작은 모델을 사용할 때 REBASE와 같은 알고리즘을 사용하면 문제 해결에 있어 경쟁력 있는 정확도를 달성하면서도 비용을 크게 절감할 수 있음을 발견하였습니다.

향후 연구에서는 더 다양한 데이터셋와 문제 유형에 대해 이런 접근 방식을 확장하고, 보다 복잡한 수학적 문제에 대한 언어 모델의 능력을 더욱 심도 있게 탐구할 계획입니다.

이 연구에서는 언어 모델을 사용한 문제 해결을 위한 최적 계산 인퍼런스에 대한 종합적인 실험 분석을 수행했습니다. 다양한 모델 크기에서 인퍼런스 동안의 계산 스케일링 효과를 조사했으며, 계산 예산이 제한적일 때는 작은 모델이 선호될 수 있음을 발견했습니다. 또한 REBASE라는 새로운 트리 검색 방법을 도입하여 샘플링 방법과 MCTS보다 계산적으로 더 최적화된 것을 보였습니다.

한계점

실험은 주로 수학 문제 해결 과제에 초점을 맞추었으며, 모델은 주로 MetaMath 데이터셋을 사용하여 훈련되었습니다. 다양한 훈련 데이터셋이 수학 문제 해결을 위한 최적 계산 인퍼런스 전략의 성능과 효율성에 미치는 영향을 조사하는 것은 향후 연구 방향으로 가치가 있습니다.

Appendix

A. Omitted Proofs

A.1. Theorem 1의 증명

Theorem 1은 수학적인 통계와 확률론을 기반으로 하여 언어 모델의 출력이 어떻게 최종적으로 가장 가능성이 높은 답변을 선택하게 되는지 설명합니다.

Theorem 1에서 답변은 $L$ 토큰보다 짧아야 한다는 가정 하에 모든 가능한 답변의 집합을 $\mathcal{A} = {v \mid \|v\| \leq L}$로 정의합니다.

언어 모델 $\pi$가 주어진 질문 $x$에 대해 답변 $y$를 출력할 확률을 $\tilde{\pi}(y \mid x)$로 표현하며, 이는 “reasoning paths”를 통합한 마진 확률로 다음과 같습니다.

1. 가능한 답변 집합과 확률 함수 정의

• 가능한 모든 답변의 집합 $\mathcal{A} = {v \mid \|v\| \leq L}$를 정의합니다. 이는 답변이 될 수 있는 모든 토큰의 조합을 포함합니다.

• 언어 모델 $\pi$에 의해 주어진 입력 $x$에 대한 답변 $y$의 출력 확률을 $\tilde{\pi}(y \mid x)$로 정의합니다. 이 확률은 모든 reasoning paths를 통합한 결과입니다.

  \[\tilde{\pi}(y \mid x) = \sum_{r \in \mathcal{V}^*} \pi(y \mid x)\]

2. 최적 답변과 차이 정의

• \(\tilde{\pi}(y \mid x)\)를 최대화하는 답변 $y^*$를 선택합니다.

  \[y^* = \arg\max_{y \in \mathcal{A}} \tilde{\pi}(y \mid x)\]

• $y^*$와 그 외의 다른 답변 $y’$ 사이의 확률 차이 $\delta$를 정의합니다.

  \[\delta = \tilde{\pi}(y^* \mid x) - \max_{y \in \mathcal{A} \setminus \{y^*\}} \tilde{\pi}(y \mid x)\]

3. 표본 통계와 이벤트 정의

• 모델이 처음 $n$개의 표본에서 $y$를 답변으로 제시한 횟수를 \(f_n(y)\)로 정의합니다.
• 다수결 보팅가 $y^*$를 출력하지 않는 이벤트를 $E_n$으로 정의합니다. $E_n$은 \(f_n(y) \geq f_n(y^*)\)인 $y$가 존재할 때 발생합니다.

4. 확률의 상한 추정

• 유니온 바운드를 사용하여 $E_n$의 확률을 추정합니다.

  \[P(E_n) \leq \\|\mathcal{A}\\| \cdot P(f_n(y') \geq f_n(y^*))\]

• $f_n(y^*) - f_n(y’)$는 기대값이 $\delta$인 $n$개의 독립 동일 분포(i.i.d.) 확률 변수의 합으로 간주되며, Hoeffding의 부등식을 적용하여 다음과 같이 표현합니다.

  \[P(f_n(y') \geq f_n(y^*)) \leq \exp\left(-\frac{n\delta^2}{2}\right)\]

5. Borel-Cantelli Lemma의 적용

• 위의 부등식을 사용하여 모든 $n$에 대한 $E_n$의 합이 유한함을 보여주고, 거의 확실하게 $n \to \infty$에서 $E_n = 0$임을 보여줍니다. 이는 $n$이 충분히 클 때 $y^*$가 거의 확실하게 다수결 보팅의 결과가 됨을 의미합니다.

6. 데이터셋에 대한 일반화

• 위의 논증을 데이터셋 $\mathcal{D}$의 모든 예제에 적용하고 결과를 결합하여 거의 확실한 수렴을 증명합니다. 이는 언어 모델이 다수결 보팅를 통해 각 입력에 대해 가장 가능성 높은 답변을 선택하게 됨을 보여줍니다.

이 증명은 언어 모델이 주어진 입력에 대해 가장 가능성이 높은 답변을 선택하는 메커니즘이 어떻게 통계적으로 보장되는지를 수학적으로 보여줍니다. 이는 인퍼런스 과정에서의 확률적 행동을 이해하는 데 중요한 기초가 됩니다.

위와 같이 Theorem 1은 $\lim_{n \to \infty} \text{acc}_{MV}^n({(x, y)}; \pi) = 1$ (almost surely)임을 Theorem하고, 다수결 보팅를 사용한 경우에 언어 모델이 가장 가능성이 높은 답변을 거의 확실하게 선택하게 됨을 보입니다.

A.2. Theorem 2의 증명

Theorem 2의 증명은 Theorem 1의 증명 구조를 따르며, Theorem 2의 경우 가중치가 포함된 확률을 고려한다는 것이 약간 다릅니다.

1. 확률 함수 수정

Theorem 1에서는 $\tilde{\pi}(y \mid x)$를 언어 모델 $\pi$에 의해 주어진 입력 $x$에 대한 답변 $y$의 출력 확률로 정의했습니다. Theorem 2에서는 이 확률을 보상 모델 $\rho$를 포함하여 수정합니다.

이 확률은 언어 모델의 출력과 보상 모델의 가중치를 결합한 것으로, 각 답변의 품질을 반영합니다.

2. 최적화된 답변과 확률 차이

• $\tilde{\pi}(y \mid x)$를 최대화하는 답변 $y^*$를 선택합니다.

  \[y^* = \arg\max_{y \in \mathcal{A}} \tilde{\pi}(y \mid x)\]

• $y^*$와 다른 답변들 사이의 확률 차이 $\delta$를 다음과 같이 정의합니다.

  \[\delta = \tilde{\pi}(y^* \mid x) - \max_{y \in \mathcal{A} \setminus \{y^*\}} \tilde{\pi}(y \mid x)\]

3. 확률의 상한 추정 및 Borel-Cantelli Lemma(보렐-칸텔리 보조정리)

• Hoeffding의 부등식을 적용하여 다수결 보팅가 $y^*$를 선택하지 않을 확률의 상한을 계산합니다.

  \[P(f_n(y') \geq f_n(y^*)) \leq \exp\left(-\frac{n\delta^2}{2}\right)\]

• 모든 $n$에 대한 이 확률의 합이 유한함을 보여주고, Borel-Cantelli Lemma를 사용하여 $n \to \infty$에서 $E_n = 0$이 거의 확실하게 성립함을 보여줍니다. 이는 $y^*$가 거의 확실하게 다수결 보팅의 결과가 됨을 의미합니다.

4. 일반화 및 데이터셋 적용

• 위의 논증은 데이터셋 $\mathcal{D}$의 각 예제에 적용하고 결과를 결합하여 거의 확실한 수렴을 증명합니다.

B. MCTS 상세 설명

몬테 카를로 트리 검색(MCTS) 알고리즘은 복잡한 의사 결정 과정에서 효과적인 최적화 기법으로 사용되며, MCTS의 기본 단계는 다음과 같습니다.

1. 선택

• 루트 노드에서 시작하여, 가장 높은 UCT(Upper Confidence Bound applied to Trees) 값을 제공하는 자식 노드를 반복적으로 선택합니다.

• UCT 공식

  \[UCT(s) = Q(s) + C \sqrt{\frac{\ln(N(\text{Parent}(s)))}{N(s)}}\]

  $Q(s)$는 노드 $s$의 품질 점수, $N(s)$는 노드 $s$의 방문 횟수, $\text{Parent}(s)$는 노드 $s$의 부모 노드, $C$는 탐험 수준을 결정하는 상수

2. 확장 및 평가

• 비종단 노드 $s$에 도달하면, 여러 자식 노드를 생성하여 확장합니다.
• 각 자식 노드 $c$는 값 함수 $V(c)$를 사용하여 평가되며, 이는 노드 $c$에서 시퀀스를 계속하는 잠재적 품질을 예측합니다.

3. 역전파

• 평가 후, 선택된 노드에서 루트 노드까지 경로상의 모든 노드에 대해 UCT 값과 방문 횟수를 업데이트합니다.

[참고자료 1] Borel–Cantelli Lemma

Borel–Cantelli Lemma는 확률 이론에서 사건 시퀀스의 장기적인 발생 가능성을 평가하는 데 주로 사용됩니다. 이 법칙은 확률이 0 또는 1이 될 조건을 설명하며, 제로-원 법칙(zero-one laws)의 유명한 예로, Kolmogorov의 제로-원 법칙과 Hewitt–Savage 제로-원 법칙과 같은 다른 사례들과 함께 소개되며, 독립적인 사건의 시퀀스뿐만 아니라 다양한 응용 분야에서 활용됩니다.

Kolmogorov의 제로-원 법칙 Kolmogorov의 제로-원 법칙은 확률 이론에서 극한에 관련된 독립 사건들의 확률이 ‘0’ 또는 ‘1’이 되는 현상을 설명하며, 일련의 독립적인 확률 변수들에 대한 무한히 많은 확률 변수의 값을 알더라도 그 결과를 결정할 수 없는 사건인 ‘테일 이벤트’(tail event)에 적용됩니다. 예를 들어, 동전 던지기에서 무한히 많은 동전 던지기 중 공정한 동전이 무한히 많이 앞면이 나오는 사건은 테일 이벤트에 해당하며, 이 사건의 확률은 0 또는 1로 ‘(거의) 확실하게’ 발생하거나 ‘(거의) 확실하게’ 발생하지 않음을 의미합니다.

Hewitt–Savage 제로-원 법칙 Hewitt과 Savage의 제로-원 법칙은 교환 가능한(invariant) 확률 변수의 시퀀스에 적용됩니다. 교환 가능한 확률 변수들은 변수들의 순서를 변경해도 그 합동 확률 분포가 동일하게 유지되는 변수들입니다. 이 법칙은 교환 가능한 확률 변수들에 대해 테일 이벤트의 확률이 0 또는 1이 됨을 언급합니다. 이는 변수들의 순서를 바꾸어도 그 결과에 영향을 미치지 않으므로, 그 결과가 ‘(거의) 확실하게’ 발생하거나 ‘(거의) 확실하게’ 발생하지 않음을 의미합니다.

Borel–Cantelli Lemma의 정의

확률 공간에서 일련의 사건 $E_1, E_2, …$이 주어졌을 때, Borel–Cantelli Lemma는 다음과 같이 명시됩니다.

• Borel–Cantelli Lemma (First Part)

  만약 사건들의 확률의 합이 유한하다면,

  \[\sum_{n=1}^\infty \Pr(E_n) < \infty,\]

  그렇다면 무한히 많은 사건들이 발생할 확률은 0입니다.

  \[\Pr(\limsup_{n \to \infty} E_n) = 0.\]

  $\limsup_{n \to \infty} E_n$ (limit supremum)은 무한히 자주 발생하는 결과의 집합을 나타내며, 정의는 다음과 같습니다. \(\limsup_{n \to \infty} E_n = \bigcap_{n=1}^\infty \bigcup_{k=n}^\infty E_k.\)

  예를 들어, 확률 변수의 시퀀스 $(X_n)$에서 각각 $Pr(X_n = 0) = 1/n^2$의 확률로 $X_n = 0$이 발생한다고 가정하면, 이 시퀀스에서 $X_n = 0$이 무한히 많이 발생할 확률은 다음과 같이 계산됩니다. 확률의 합이 $\pi^2/6$로 수렴하므로, Borel–Cantelli Lemma에 따라 $X_n = 0$이 무한히 발생할 확률은 0입니다.

• 사건 시퀀스 설정

  사건의 합집합 $\bigcup_{n=N}^\infty E_n$은 $N$이 증가함에 따라 감소합니다.

  \[\bigcup_{n=1}^\infty E_n \supseteq \bigcup_{n=2}^\infty E_n \supseteq \cdots \supseteq \limsup_{n \to \infty} E_n.\]

• 확률의 연속성 이용

  확률의 연속성은 확률 공간에서 일련의 사건 시퀀스의 극한과 관련된 확률을 계산할 때 주로 사용되며, 확률의 연속성은 두 가지 주요 형태로 나타납니다.

  • (1) Continuity from above: 사건 시퀀스가 감소하며 모든 사건이 포함하는 최소 사건으로 수렴할 때, 그 확률 역시 이 극한 사건의 확률로 수렴한다.

    \[\Pr\left(\bigcap_{n=1}^\infty A_n\right) = \lim_{n \to \infty} \Pr(A_n) \quad \text{if } A_1 \supseteq A_2 \supseteq A_3 \supseteq \cdots\]

  • (2) Continuity from below: 사건 시퀀스가 증가하며 모든 사건이 포함하는 최대 사건으로 수렴할 때, 그 확률 역시 이 극한 사건의 확률로 수렴한다.

    \[\Pr\left(\bigcup_{n=1}^\infty A_n\right) = \lim_{n \to \infty} \Pr(A_n) \quad \text{if } A_1 \subseteq A_2 \subseteq A_3 \subseteq \cdots\]

  위의 확률의 연속성을 이용해서 다음과 같이 정리할 수 있습니다.

  \[\Pr(\limsup_{n \to \infty} E_n) = \lim_{N \to \infty} \Pr(\bigcup_{n=N}^\infty E_n).\]

• 부분가법성 활용

  부분가법성은 확률 이론에서 사건들의 합집합에 대한 확률을 추정할 때 사용되는 개념으로 서로 배타적이지 않은(즉, 겹칠 수 있는) 여러 사건에 대해 그 합집합의 확률을 평가할 때 주로 사용됩니다. 구체적으로, 두 개 이상의 사건의 합집합의 확률은 각각의 사건 확률의 합보다 작거나 같다는 것을 의미하며 다음과 같이 표현할 수 있습니다.

  \[\Pr\left(\bigcup_{i=1}^n A_i\right) \leq \sum_{i=1}^n \Pr(A_i).\]

  이 부분가법성을 통해 정리하면, 다음과 같이 표현할 수 있습니다.

  \[\Pr(\bigcup_{n=N}^\infty E_n) \leq \sum_{n=N}^\infty \Pr(E_n).\]

• 마지막으로 원래 가정에 따르면,

  \[\sum_{n=1}^\infty \Pr(E_n) < \infty.\]

  이 합이 수렴하므로,

  \[\lim_{N \to \infty} \sum_{n=N}^\infty \Pr(E_n) = 0,\]