PPO
- Related Project: Private
- Category: Paper Review
- Date: 2023-10-28
Proximal Policy Optimization Algorithms
- url: https://arxiv.org/abs/1707.06347
- pdf: https://arxiv.org/pdf/1707.06347
- abstract: We propose a new family of policy gradient methods for reinforcement learning, which alternate between sampling data through interaction with the environment, and optimizing a “surrogate” objective function using stochastic gradient ascent. Whereas standard policy gradient methods perform one gradient update per data sample, we propose a novel objective function that enables multiple epochs of minibatch updates. The new methods, which we call proximal policy optimization (PPO), have some of the benefits of trust region policy optimization (TRPO), but they are much simpler to implement, more general, and have better sample complexity (empirically). Our experiments test PPO on a collection of benchmark tasks, including simulated robotic locomotion and Atari game playing, and we show that PPO outperforms other online policy gradient methods, and overall strikes a favorable balance between sample complexity, simplicity, and wall-time.
Contents
- Proximal Policy Optimization Algorithms
TL;DR
- 정책 최적화와 확률 비율의 클리핑: 새로운 목적함수를 통해 정책의 데이터 효율성 및 안정성 개선
- 수학적 설명과 실험적 증명: 클리핑된 확률 비율을 사용하여 과도한 정책 업데이트 방지 및 성능 향상
- 비교 및 평가: 다양한 기준과 데이터셋을 통해 기존 알고리즘과의 성능 비교
- Environment과의 상호작용을 통해 데이터를 샘플링하고, Stochastic Gradient Ascent(GSA)을 사용해 “Surrogate” Objective Function을 최적화하는 강화 학습을 위한 새로운 정책 기울기 방법을 제안
- 표준 정책 기울기 방법(Standard Policy Gradient Methods)은 데이터 샘플당 한 번의 기울기 업데이트를 수행하지만, 여러 번에 걸친 미니 배치 업데이트를 가능하게 하는 새로운 목적함수를 제안
- 근거리 정책 최적화(Proximal Policy Optimization, PPO)라고 부르는 이 새로운 방법은 신뢰 영역 정책 최적화(Trust Region Policy Optimization, TRPO)의 몇 가지 장점을 가지고 있지만, 구현이 훨씬 간단하고 일반적이며 (경험적으로) 샘플 복잡성이 더 우수함을 주장
- 시뮬레이션된 로봇 동작과 아타리 게임 플레이를 포함한 다양한 벤치마크 작업에서 PPO를 테스트한 결과, PPO가 다른 온라인 정책 그라데이션 방법보다 성능이 뛰어나며 전반적으로 샘플 복잡성, 단순성, 월타임 간에 유리한 균형을 이루고 있는 것으로 나타남을 보고함.
[논문의 주장 및 근거]
이 논문은 강화 학습에서 신경망 함수 근사자를 사용하는 방법 중 하나인 Proximal Policy Optimization (PPO)을 소개하고, 기존 방법들과의 차별점을 명시한다. PPO는 데이터 효율성과 신뢰성을 개선하며, 단순한 일차 최적화만을 사용하여 성능을 향상시킨다는 주장을 제기한다.
이 방법은 확률 비율 클리핑을 통해 정책의 성능에 대한 비관적 추정을 형성하고, 여러 에포크에 걸쳐 반복 최적화를 수행함으로써 일반 Policy 그래디언트와 신뢰 영역 방법(TRPO)의 장점을 결합한다. 이 논문은 강화 학습(RL)에서 새로운 방법을 제안하여 특히 데이터 효율성과 다양한 환경에서의 성능 개선을 목표하며, 본 논문의 수식들은 대부분 정책의 성능을 정량화하고, 정책 업데이트 방향과 크기를 결정한다.
[방법]
PPO는 다음과 같은 스텝을 통해 구현된다.
- Policy 그래디언트 추정: Policy 그래디언트를 계산하고 이를 확률적 그래디언트 상승 알고리즘에 적용.
- 클리핑된 목적함수: 확률 비율을 클리핑하여 정책 업데이트 시 과도한 변동을 제한.
-
반복 최적화: 샘플링된 데이터를 이용해 여러 에포크 동안 최적화를 수행.
-
정책 최적화 방법 개선
- Policy 그래디언트 방법: 이는 정책을 평가하고 개선하는 기본 메커니즘으로, 정책 파라미터를 업데이트하기 위해 경험적 평균을 이용한 그래디언트 상승을 사용한다. 식 (1)과 (2)에서는 정책의 로그-우도에 대한 그래디언트를 계산하여 정책을 개선하는 과정을 설명한다.
- 신뢰 영역 방법 (TRPO): 식 (3)과 (4)는 이전 정책 대비 새 정책의 성능을 향상시키면서 KL Divergence을 제한하는 구조를 제공하여, 파라미터 업데이트시 발생할 수 있는 급격한 변화를 방지한다.
-
클리핑된 대리 목적 패스 (Clipped Surrogate Objective)
- 이는 식 (7)에서 설명된 바와 같이, 확률 비율을 특정 범위 안에서만 변동하게 제한하는 방식을 통해 과도한 업데이트를 방지하고, 알고리즘의 안정성을 높이는 데 목적이 있으며, 특히 $\epsilon$ 값을 사용하여 확률 비율의 상한과 하한을 설정한다.
-
적응형 KL 페널티 계수
- 식 (8)에서는 KL Divergence을 통해 정책 업데이트를 조절하는 또 다른 방법을 제안한다. 이는 목표 KL Divergence에 가깝도록 페널티 계수 $\beta$를 조정함으로써 정책 업데이트의 크기를 파인튜닝할 수 있습니다.
-
알고리즘의 실행 및 평가
- 구체적인 알고리즘 실행 방법 및 평가는 논문의 후반부에서 다루고 있으며, 특히 PPO 알고리즘은 각 시행에서 데이터를 수집하고 이를 기반으로 정책을 반복적으로 개선한다. 실제 환경 테스트에서는 여러 강화 학습 작업에 대해 PPO가 기존 방법들을 능가하는 것을 보여줍니다.
[주요 보고]
- 성능 개선: 연속 제어 작업 및 아타리 게임에서 PPO는 다른 알고리즘들보다 우수한 성능을 보임.
- 간소화 및 호환성: 복잡성과 노이즈에 강하며, 다양한 아키텍처와 호환됨.
- 비교 연구: 기존 방법들과의 비교를 통해 PPO의 우수성과 적용 가능성을 입증.
결론 및 향후 지침
PPO는 강화 학습 분야에서 신뢰 영역 방법의 안정성과 간단함을 결합한 효과적인 방법으로 다양한 문제 설정에서 적용 가능하며, 특히 고차원 연속 제어 문제와 복잡한 게임 환경에서 향상된 성능을 보인다. 연구자들은 기존의 Policy 그래디언트 방법에 소소한 수정을 통해 PPO를 적용할 수 있으며, 이를 통해 학습 효율성과 정책의 안정성을 동시에 개선할 수 있다.
1. 서론
최근 몇 년 간 신경망 함수 근사자를 사용하는 강화 학습 방법이 여러가지 제안되었다. 주요 대안으로는 깊은 Q-learning, 일반 Policy 그래디언트 방법, 그리고 신뢰 영역/자연 Policy 그래디언트 방법들이 있다.
그러나 큰 모델과 병렬 구현에서 확장 가능하며, 데이터 효율성이 높고, 하이퍼파라미터 튜닝 없이도 다양한 문제에서 성공적인 방법을 개발할 여지가 남아 있다. 함수 근사를 사용한 Q-learning은 많은 간단한 문제에서 실패하고 이해하기 어렵고, 일반 Policy 그래디언트 방법은 데이터 효율성과 강건성이 낮으며, 신뢰 영역 정책 최적화(TRPO)는 상대적으로 복잡하고 노이즈(드롭아웃 등)나 파라미터 공유(정책과 가치 함수 사이, 또는 보조 작업과)를 포함한 아키텍처와 호환되지 않는다.
이 논문은 데이터 효율성과 TRPO의 신뢰할 수 있는 성능을 달성하면서, 오직 일차 최적화만을 사용하는 알고리즘을 소개함으로써 현재 상황을 개선하고자 한다. 확률 비율을 클리핑한 새로운 목적함수를 제안하며, 이는 정책의 성능에 대한 비관적 추정(즉, 하한)을 형성한다.
정책을 최적화하기 위해, 정책에서 데이터를 샘플링하고 샘플링된 데이터에 대해 여러 에포크 동안 최적화를 수행하는 것을 번갈아 가며 진행한다. 실험에서 서로 다른 버전의 대리 목적 패스 함수의 성능을 비교하며, 확률 비율이 클리핑된 버전이 가장 우수한 성능을 보인다는 것을 발견했다.
또, PPO를 문헌의 여러 이전 알고리즘들과 비교한다. 연속 제어 작업에서, 비교한 알고리즘들보다 더 나은 성능을 보인다. 아타리에서 A2C보다 샘플 복잡성 측면에서 더 나은 성능을 보이며 ACER와 유사하지만 훨씬 간단함을 확인한다.
2. 배경: 정책 최적화(Policy Optimization)
2.1 Policy 그래디언트 방법(Policy 그래디언트 Methods)
Policy 그래디언트 방법은 Policy 그래디언트의 추정값을 계산하고 이를 확률적 그래디언트 상승 알고리즘에 적용하여 작동한다. 가장 널리 사용되는 그래디언트 추정식은 다음과 같은 형태를 가진다.
\[\hat{g} = \hat{\mathbb{E}}[\nabla_{\theta} \log \pi_{\theta}(a_t \| s_t) \hat{A}_t] \tag{1}\]수식에서 $\pi_{\theta}$는 확률적 정책이며, $\hat{A}_t$는 시간 단계 $t$에서의 advantage 함수 추정값이다. 수식에서 기대값 $\hat{\mathbb{E}}[\ldots]$는 샘플링과 최적화를 번갈아 가며 진행하는 알고리즘에서 유한 배치의 샘플에 대한 경험적 평균을 나타낸다. 자동 미분 소프트웨어를 사용하는 구현은 그래디언트가 Policy 그래디언트 추정식인 목적함수를 구성함으로써 작동하며, 추정식 $\hat{g}$는 목적함수를 미분함으로써 얻어진다.
\[\mathcal{L}_{\text{PG}}( heta) = \hat{\mathbb{E}}[\theta \log \pi_{\theta}(a_t \| s_t) \hat{A}_t] \tag{2}\]이 손실 $\mathcal{L}_{\text{PG}}$에 대해 같은 궤적을 사용하여 여러 단계의 최적화를 수행하는 것은 매력적이지만, 이렇게 할 경우 잘 정당화되지 않으며, 경험적으로 종종 파괴적으로 큰 정책 업데이트로 이어졌다(6.1절 참조; 결과는 표시되지 않았지만 "클리핑 또는 페널티 없음" 설정보다 비슷하거나 더 나빴다).
[반복 최적화 실패 관련 색인마킹]
2.2 신뢰 영역 방법(Trust Region Methods)
TRPO에서는 정책 업데이트의 크기에 대한 제약 조건을 만족하는 목적함수(“대리” 목적함수라고 함)를 최대화한다. 총체적으로는 다음을 최대화한다.
\[\theta \, \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t \\| s_t)}{\pi_{\theta_{\text{old}}}(a_t \\| s_t)} \hat{A}_t \right] \tag{3}\]제약 조건에 따르면:
\[\hat{\mathbb{E}} \left[ \text{KL}[\pi_{\theta_{\text{old}}}(\cdot \\| s_t), \pi_{\theta}(\cdot \\| s_t)] \right] \leq \delta \tag{4}\]수식에서 $\theta_{\text{old}}$는 업데이트 전의 정책 파라미터 벡터이다. 이 문제는 목적함수에 대한 선형 근사와 제약 조건에 대한 이차 근사를 만든 후, 공역 그래디언트 알고리즘을 사용하여 효율적으로 근사적으로 해결할 수 있다.
켤레기울기법 또는 공역기울기법(Conjugate Gradient Method)이란 수학에서 대칭인 양의 준정부호행렬(positive-semidefinite matrix)을 갖는 선형계의 해를 구하는 수치 알고리즘
TRPO가 제안하는 이론은 제약 대신 페널티을 사용하는 것을 제안한다. 즉, 다음과 같은 무제약 최적화 문제를 해결한다.
\[\text{maximize} \, \theta \, \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t \\| s_t)}{\pi_{\theta_{\text{old}} }(a_t \\| s_t)} \hat{A}_t - \beta \text{KL}[\pi_{\theta_{\text{old}}}(\cdot \\| s_t), \pi_{\theta}(\cdot \\| s_t)] \right] \tag{5}\]수식에서 $\beta$는 계수로, 어떤 대리 목적 패스 함수가 상태에 대한 최대 KL을 계산하는 대신 평균을 형성하고, 정책 $\pi$의 성능에 대한 하한(즉, 비관적 경계)을 형성한다는 사실에서 비롯된다.
TRPO는 단일 $\beta$ 값이 다양한 문제에서 또는 학습 과정에서 변화하는 문제의 특성 내에서도 잘 작동하기 어려운 경우가 많기 때문에 페널티 대신 하드 제약을 하므로 일차 알고리즘을 사용하여 TRPO의 단조적 개선을 모방하는 목표를 달성하기 위해, 단순히 고정된 페널티 계수 $\beta$를 선택하고 SGD로 페널티가 있는 목적함수(방정식 5)를 최적화하는 것으로는 충분하지 않으며, 추가적으로 수정해야한다.
3. 클리핑된 대리 목적 패스
엡실론 하이퍼파라미터: \(\epsilon = 0.2\).
목적 동기(Objective Motivation): min 내의 첫 번째 항은 LCPI이다. 두 번째 항, \(\text{clip}(r_t( heta), 1-\epsilon, 1+\epsilon) \hat{A}_t\),은 확률 비율을 클리핑하여 \(r_t\)가 \([1-\epsilon, 1+\epsilon]\)의 구간 밖으로 이동하는 것에 대한 유인을 제거한다. 클리핑된 목적과 클리핑되지 않은 목적의 최소값을 취하므로, 최종 목적은 클리핑되지 않은 목적에 대한 하한(즉, 비관적 경계)이다. 이는 목적을 개선할 때는 확률 비율의 변화를 무시하고, 목적을 악화시킬 때는 이를 포함하는 것을 보장한다.
LCLIP에 대한 자세한 내용
- \(L_{\text{CLIP}}( heta) = L_{\text{CPI}}( heta)\)는 \(\theta_{\text{old}}\) 주변의 일차적으로 동일하지만, \(\theta\)가 \(\theta_{\text{old}}\)에서 멀어짐에 따라 다르다.
[본문]
$ r_t( heta) $는 확률 비율을 나타낸다.
\[r_t( heta) = \frac{\pi_{\theta}(a_t \\| s_t)}{\pi_{\theta_{\text{old}}}(a_t \\| s_t)}\]따라서 $ r( heta_{\text{old}}) = 1 $.
TRPO는 “대리” 목적을 최대화한다.
\[\mathcal{L}_{\text{CPI}}( heta) = \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t \\| s_t)}{\pi_{\theta_{\text{old}}}(a_t \\| s_t)} \hat{A}_t \right] \tag{6}\]CPI의 첨자는 보수적 정책 반복을 나타낸다[Kleinman02], 여기에서 이 목적이 제안되었다. 제약 없이 $\mathcal{L}_{\text{CPI}}$의 최대화는 과도한 정책 업데이트를 초래할 것이므로, 이제 $ r( heta) $가 1에서 멀어지는 정책의 변경을 처벌하는 목적 수정을 고려한다.
제안하는 주된 목적은 다음과 같다.
\[\mathcal{L}_{\text{CLIP}}( heta) = \hat{\mathbb{E}} \left[ \min \left( r_t( heta) \hat{A}_t, \, \text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] \tag{7}\]수식에서 $\epsilon$는 하이퍼파라미터이며, 예를 들어, $\epsilon = 0.2$이다.
이 목적의 동기는 다음과 같다.
- min 내부의 첫 번째 항은 \(\mathcal{L}_{\text{CPI}}\)이다.
- 두 번째 항, \(\text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t\)은 확률 비율을 클리핑함으로써 \(r_t\)가 \([1 - \epsilon, 1 + \epsilon]\)의 구간 밖으로 이동하는 것에 대한 유인을 제거한다.
- 마지막으로, 클리핑된 목적과 클리핑되지 않은 목적의 최소값을 취하므로, 최종 목적은 클리핑되지 않은 목적에 대한 하한(즉, 비관적 경계)이다.
이 체계를 통해 목적을 개선할 때는 확률 비율의 변화를 무시하고, 목적을 악화시킬 때는 이를 포함하는 것을 보장한다. 주목할 점은 \(\mathcal{L}_{\text{CLIP}}( heta) = \mathcal{L}_{\text{CPI}}( heta)\)는 \(\theta_{\text{old}}\) 주변의 일차적으로 동일하지만, $\theta$가 \(\theta_{\text{old}}\)에서 멀어짐에 따라 다르다는 것이다.
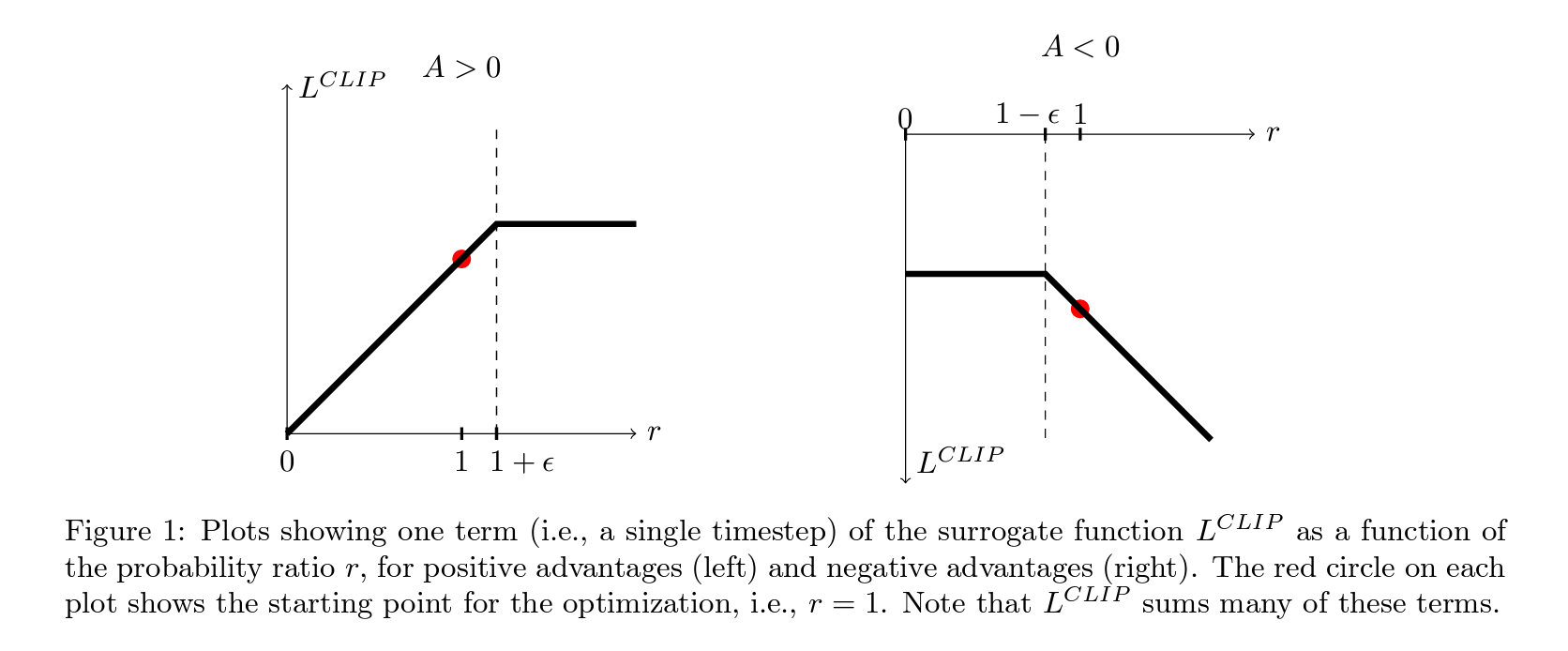
Figure 1은 확률 비율 $r$의 함수로서 대리 함수 $L_{\text{CLIP}}$의 단일 항(즉, 단일 시간 단계)을 플롯한다.
왼쪽은 긍정적인 advantage을 가진 경우이고, 오른쪽은 부정적인 advantage을 가진 경우이다. 각 플롯에서 최적화의 시작점을 나타내는 빨간 원, 즉 $r = 1$을 보여준다. 주목할 점은 $L_{\text{CLIP}}$은 이런 많은 항을 합산한다는 것이다.
4. 적응형 KL 페널티 계수
대안적 접근 방식: 클리핑된 대리 목적 패스의 대안으로 사용되거나 이와 함께 사용될 수 있는 다른 접근 방식은 KL Divergence에 대한 페널티을 사용하고, 정책 업데이트마다 목표 KL Divergence \(d_{\text{targ}}\) 값을 달성하기 위해 페널티 계수를 조정하는 것이다. 실험에서는 KL 페널티이 클리핑된 대리 목적 패스보다 성능이 떨어졌지만, 중요한 베이스 라인으로서 여기에 포함시켰다.
다음과 같이 클리핑된 대리 목적 패스 함수와 함께 또는 대안으로 사용되며, 이 접근 방식은 KL Divergence에 대한 페널티을 포함하고, 정책 업데이트마다 목표 KL Divergence 값을 달성하기 위해 페널티 계수를 조정한다.
단계 포함
- KL 페널티 목적함수 \(L_{\text{KL-PEN}}( heta)\) 최적화
- 목표 KL Divergence에서의 차이에 따라 \(\beta\) 조정
방정식
\[L_{\text{KL-PEN}}( heta) = \hat{E}_t \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)} \right] - \beta \text{KL}[\pi_{\theta_{\text{old}}}(\cdot | s_t), \pi_{\theta}(\cdot | s_t)]\]이 알고리즘의 가장 간단한 구현에서는 각 정책 업데이트에서 다음 단계를 수행한다.
- 몇 epoch 동안의 미니배치 SGD를 사용하여 KL 페널티 목적함수 \(L_{\text{KLPEN}}( heta)\)를 최적화한다.
- \(d = \hat{E}_t[\text{KL}[\pi_{\theta_{\text{old}}}(\cdot \\| s_t), \pi_{\theta}(\cdot \\| s_t)]]\)를 계산한다.
- 만약 \(d < d_{\text{targ}}/1.5\)이면, \(\beta \leftarrow \beta/2\)
- 만약 \(d > d_{\text{targ}} \times 1.5\)이면, \(\beta \leftarrow \beta \times 2\)
다음 정책 업데이트에 사용되는 업데이트된 \(\beta\)는 이 방식을 통해 KL Divergence이 \(d_{\text{targ}}\)와 많이 다른 경우가 드물게 발생하지만, 이런 경우는 드물고 \(\beta\)는 빠르게 조정된다. 위의 1.5와 2는 경험적으로 선택된 값이지만, 알고리즘은 이런 값에 민감하지 않다. \(\beta\)의 초기 값은 또 다른 하이퍼파라미터이지만, 알고리즘이 이를 빠르게 조정하기 때문에 실제로는 중요하지 않다.
\[\begin{align} L_{\text{KL-PEN}}( heta) &= \hat{E}_t \left[ \pi_{\theta}(a_t\\|s_t) \pi_{\theta_{\text{old}}}(a_t\\|s_t) - \beta \text{KL}[\pi_{\theta_{\text{old}}}( \cdot \\| s_t), \pi_{\theta}( \cdot \\| s_t)] \right] \tag{8} \end{align}\]5. 알고리즘
이전 섹션의 대리 손실은 전형적인 Policy 그래디언트 구현에 약간의 변경을 가하여 계산 및 차별화될 수 있다. 자동 미분을 사용하는 구현에서는 \(L_{\text{PG}}\) 대신 \(L_{\text{CLIP}}\) 또는 \(L_{\text{KLPEN}}\) 손실을 구성하고, 이 목적에 대해 여러 단계의 확률적 그래디언트 상승을 수행한다.
분산 감소된 보상(advantage) 함수 추정기를 계산하는 대부분의 기법은 학습된 상태-값 함수 \(V(s)\)를 사용하는데 예를 들어, 일반화된 advantage 추정 또는 과거 연구에서의 Finite-Horizon Estimator 등이 있다. 정책과 값 함수 간에 파라미터를 공유하는 신경망 아키텍처를 사용하는 경우, 정책 대리 및 값 함수 오류 항을 결합한 손실 함수를 사용해야 한다. 이 목적은 과거 작업에서 제안된 것처럼 충분한 탐험을 보장하기 위해 엔트로피 보너스를 추가함으로써 더욱 확장될 수 있다.
이런 항을 결합하면, 다음 목적함수가 (대략적으로) 각 반복에서 최대화된다.
\[L_{\text{CLIP+VF+S}}( heta) = \hat{E}_t[L_{\text{CLIP}}( heta) - c_1 L_{\text{VF}}( heta) + c_2 S[\pi_{\theta}](s_t)],\]수식에서 \(c_1, c_2\)는 계수이며, \(S\)는 엔트로피 보너스를 나타낸다.
손실 함수 \(L_{\text{VF}}( heta)\)는 제곱 오류 손실로 정의된다.
\[L_{\text{VF}}( heta) = (V_{\theta}(s_t) - V_{\text{targ}}(s_t))^2 \tag{9}\]최근 연구에서 인기를 얻은 Policy 그래디언트 구현 스타일 중 하나는 정책을 \(T\) 타임스텝(수식에서 \(T\)는 에피소드 길이보다 훨씬 작음) 동안 실행하고, 수집된 샘플을 업데이트에 사용하는 것이다. 이 스타일은 타임스텝 \(T\)를 넘어서지 않는 advantage 추정기를 필요로 한다. 사용된 추정기는 다음과 같다.
\[\hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + \ldots + \gamma^{T-t+1} r_{T-1} + \gamma^{T-t} V(s_T) \tag{10}\]수식에서 \(t\)는 주어진 길이-\(T\) 궤적 세그먼트 내의 시간 인덱스를 지정한다. 이 선택을 일반화하면, 일반화된 advantage 추정의 축소된 버전을 사용할 수 있으며, 이는 \(\lambda = 1\)일 때 방정식 (10)으로 축소된다.
advantage 추정기 \(\hat{A}_t\)는 다음과 같이 표현된다.
\[\hat{A}_t = \delta_t + (\gamma \lambda) \delta_{t+1} + \cdots + (\gamma \lambda)^{T-t+1} \delta_{T-1} \tag{11}\]수식에서 \(\delta_t\)는 다음과 같이 정의된다.
\[\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) \tag{12}\]고정 길이 궤적 세그먼트를 사용하는 근접 정책 최적화(PPO) 알고리즘은 아래와 같다. 각 반복마다, \(N\) (병렬) 액터가 \(T\) 타임스텝의 데이터를 수집한다. 그런 다음 이 \(NT\) 타임스텝의 데이터에 대해 대리 손실을 구성하고, 미니배치 SGD(또는 일반적으로 더 나은 성능을 위해 Adam)를 사용하여 \(K\) epoch 동안 최적화한다.
PPO, Actor-Critic Style
\[\begin{align*} \text{for iteration} &= 1,2,\ldots \text{ do} \\ \text{for actor} &= 1,2,\ldots,N \text{ do} \\ &\text{Run policy } \pi_{\theta_{\text{old}}} \text{ in environment for } T \text{ timesteps} \\ &\text{Compute advantage estimates } \hat{A}_1, \ldots, \hat{A}_T \\ \text{end for} \\ &\text{Optimize surrogate } L \text{ wrt } \theta, \text{ with } K \text{ epochs and minibatch size } M \leq NT \\ &\theta_{\text{old}} \leftarrow \theta \\ \text{end for} \end{align*}\]- 알고리즘 1: PPO
- 반복=1,2,…에 대하여 수행:
- 액터=1,2,…,N에 대하여 수행:
- 환경에서 \(T\) 타임스텝 동안 정책 \(\pi_{\theta_{\text{old}}}\)를 실행한다.
- advantage 추정치 \(\hat{A}_1, ..., \hat{A}_T\)를 계산한다.
- 미니배치 SGD를 사용하여 \(\theta\)에 대한 대리 \(L\)를 최적화한다.
- 액터=1,2,…,N에 대하여 수행:
- 반복=1,2,…에 대하여 수행:
6. 실험
6.1 대리 목적함수 패스 비교
먼저, 다양한 하이퍼파라미터 아래에서 여러가지 다른 대리 목적함수 패스을 비교한다. 수식에서는 대리 목적함수 패스 $\text{L_CLIP}$을 여러가지 자연 변형 및 변형된 버전과 비교한다.
- 클리핑 또는 페널티 없음: \(L_t( heta) = r_t( heta) \hat{A}_t\)
- 클리핑: \(L_t( heta) = \min(r_t( heta) \hat{A}_t, \text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t)\)
- KL 페널티 (고정 또는 적응형): \(L_t( heta) = r_t( heta) \hat{A}_t - \beta \text{KL}[\pi_{\theta_{\text{old}}}, \pi_{\theta}] \hat{A}_t\)
KL 페널티의 경우, 고정된 페널티 계수 \(\beta\) 또는 섹션 4에서 설명한 대로 목표 KL 값을 사용하는 적응형 계수를 사용할 수 있다. 로그 공간에서 클리핑을 시도했지만 성능이 더 나아지지 않았음을 발견했다.
각 알고리즘 변형에 대해 하이퍼파라미터를 검색하는 데에는 연산 비용이 저렴한 벤치마크를 사용했다. 구체적으로, OpenAI Gym에서 구현된 7개의 시뮬레이션 로보틱스 작업을 사용했으며, 각 작업에서 백만 타임스텝의 훈련을 수행했다. 클리핑(\(\epsilon\)) 및 KL 페널티(\(\beta, d_{\text{targ}}\))에 사용된 하이퍼파라미터 외에, 다른 하이퍼파라미터는 표 3에 제공된다. 정책을 나타내기 위해, 64개의 유닛을 가진 두 개의 숨겨진 레이어와 tanh 비선형성을 사용하는 완전 연결 MLP를 사용했으며, 가변 표준 편차를 가진 가우스 분포의 평균을 출력한다. 정책과 값 함수 사이에 파라미터를 공유하지 않으며(따라서 계수 \(c1\)은 관련이 없음), 엔트로피 보너스도 사용하지 않는다. 각 알고리즘은 모든 7개 환경에서 3개의 랜덤 시드로 실행되었으며, 마지막 100 에피소드의 평균 총 보상을 계산하여 각 알고리즘의 실행을 평가했다. 각 환경의 점수를 이동 및 크기 조정하여 랜덤 정책이 0점을 주고 최상의 결과가 1로 설정되었으며, 21회 실행을 통해 각 알고리즘 설정에 대한 단일 스칼라를 생성했다.
| 알고리즘 설정 | 평균 정규화 점수 |
|---|---|
| 클리핑 또는 페널티 없음 | -0.39 |
| 클리핑, \(\epsilon = 0.1\) | 0.76 |
| 클리핑, \(\epsilon = 0.2\) | 0.82 |
| 클리핑, \(\epsilon = 0.3\) | 0.70 |
| 적응형 KL \(d_{\text{targ}} = 0.003\) | 0.68 |
| 적응형 KL \(d_{\text{targ}} = 0.01\) | 0.74 |
| 적응형 KL \(d_{\text{targ}} = 0.03\) | 0.71 |
| 고정 KL, \(\beta = 0.3\) | 0.62 |
| 고정 KL, \(\beta = 1\) | 0.71 |
| 고정 KL, \(\beta = 3\) | 0.72 |
| 고정 KL, \(\beta = 10\) | 0.69 |
표 1: 연속 제어 벤치마크 결과, 7개 환경에서 21회 알고리즘 실행에 대한 평균 정규화 점수.
6.2 연속 도메인에서 다른 알고리즘과의 비교
다음으로, PPO(섹션 3에서 “클리핑”된 대리 목적 패스 사용)를 문헌에서 연속 문제에 효과적인 것으로 간주되는 여러 다른 방법과 비교한다. 신뢰 영역 정책 최적화, 교차 엔트로피 방법(CEM), 적응
형 스텝 사이즈를 가진 일반 Policy 그래디언트, 그리고 신뢰 영역을 가진 A2C와 비교했다. PPO의 경우, 이전 섹션에서 사용된 하이퍼파라미터를 사용했으며, \(\epsilon = 0.2\)이다. PPO가 거의 모든 연속 제어 환경에서 이전 방법들을 능가하는 것을 보았다.
6.3 연속 도메인에서의 쇼케이스: 휴먼형의 달리기 및 조종
고차원 연속 제어 문제에서 PPO의 성능을 보여주기 위해, 로봇이 달리고, 조종하며, 지면에서 일어나야 하는 일련의 문제에서 훈련한다. 테스트한 작업은 다음과 같다.
- RoboschoolHumanoid: 전방 이동만.
- RoboschoolHumanoidFlagrun: 목표 위치가 매 200 타임스텝마다 또는 목표에 도달할 때마다 무작위로 변한다.
- RoboschoolHumanoidFlagrunHarder: 로봇이 입방체에 맞고 지면에서 일어나야 한다.
6.4 아타리 도메인에서 다른 알고리즘과의 비교
또한 아케이드 학습 환경 벤치마크에서 PPO를 실행하고, 잘 조정된 A2C와 ACER의 구현과 비교했다.
세 알고리즘 모두 이전에 사용된 동일한 정책 네트워크 아키텍처를 사용했다. PPO의 하이퍼파라미터는 표 5에 제공된다. 다른 두 알고리즘의 경우, 이 벤치마크에서 성능을 극대화하기 위해 조정된 하이퍼파라미터를 사용했다. 모든 49개 게임에 대한 결과 및 학습 곡선이 Appendix B에 제공된다. 다음 두 가지 점수 메트릭을 고려한다.
- 전체 훈련 기간 동안 에피소드당 평균 보상(빠른 학습을 선호함).
- 훈련의 마지막 100 에피소드 동안 에피소드당 평균 보상(최종 성능을 선호함).
표 2: 각 알고리즘이 “이긴” 게임 수 세 번의 시도에 걸친 평균 점수 메트릭을 기준으로.
| 알고리즘 | 전체 훈련 동안의 평균 보상 | 마지막 100 에피소드의 평균 보상 |
|---|---|---|
| A2C | 1 | 28 |
| ACER | 1 | 30 |
| PPO | 18 | 19 |
| 동점 | 0 | 1 |
이 구조화된 접근 방식은 원본 내용에서 논의된 실험 및 비교에 대한 명확성과 상세한 통찰력을 제공한다.
비교 연구
- 다양한 하이퍼파라미터 하에서 테스트된 여러 대리 목적 패스.
- PPO는 여러 연속 제어 환경에서 우수한 성능을 보였다.
- Figure 2 및 3: 성능 메트릭 및 학습 곡선을 보여준다.
7 결론
Proximal Policy Optimization (PPO)을 소개했다. 이 방법은 신뢰 영역 방법의 안정성 및 신뢰성과 간단함을 결합하며, 일반 설정에서 적용 가능하고 성능이 향상된다. 이 접근 방식은 전형적인 Policy 그래디언트 구현은 약간의 코드 변경이 필요하다.
[참고자료 1] Surrogate-base Optimization
서로게이트 최적화란?
서로게이트 최적화는 복잡한 목적함수의 근사 모델을 만들어 이를 최적화하는 기법으로, 이 근사 모델은 일반적으로 비용 함수와 상태 함수를 모델링합니다. 서로게이트 최적화의 핵심은 어떻게 서로게이트 모델을 구축하고, 이를 통해 최적화 문제를 어떻게 해결할지입니다.
설계 공간을 무작위로 탐색하여 얻은 샘플 데이터를 기반으로 구축한 뒤, 서로게이트 모델이 완성되면 최적화 알고리즘을 사용하여 서로게이트 모델을 기반으로 최적의 후보를 탐색합니다. 서로게이트 모델을 사용한 예측은 수치 분석 코드를 사용하는 것보다 훨씬 효율적이므로, 서로게이트 모델을 기반으로 한 탐색의 계산 비용은 일반적으로 무시할 수 있을정도로 낮은 편입니다.
 *출처: https://sksurrogate.readthedocs.io/en/latest/surrogate.html
*출처: https://sksurrogate.readthedocs.io/en/latest/surrogate.html
서로게이트 기반 최적화는 복잡하고 비용이 많이 드는 계산을 피하면서, 지역적 또는 전역적 최적점을 빠르게 찾는 최적화 방법입니다. 이 방법은 대체 모델(Surrogate model)을 활용하여 최적화하거나 혹은 본 페이지의 논문처럼 대리 함수를 설정하기도 합니다. 기존의 최적화 알고리즘(e.g., 기울기 기반 또는 진화 알고리즘)을 서브 최적화에 사용할 수 있기때문에, 복잡한 최적화 문제를 해결하는 방법 중 하나로 널리 사용되고 있습니다. 주로 고비용 또는 시간이 많이 소요되는 평가 함수를 가진 최적화 문제에 적용됩니다.
핵심 개념
- 원시 목적함수(Original Objective Function): 실제 최적화하고자 하는 복잡한 함수입니다.
- 서로게이트 모델(Surrogate Model): 원시 목적함수를 근사화하는 모델로, 보통 다항식, 인공신경망(ANN), 가우시안 프로세스 등을 사용합니다.
- 최적화(Optimization): 서로게이트 모델을 사용하여 최적의 해를 찾습니다.
서로게이트 모델 구성
일반적으로 서로게이트 모델은 다음과 같은 형태의 함수로 표현됩니다.
\[S(x; \theta) \approx f(x)\]\(S\)는 서로게이트 모델, \(f\)는 원시 목적함수, \(x\)는 입력 변수, \(\theta\)는 모델 파라미터입니다.
최적화 과정
서로게이트 모델을 사용한 최적화 과정은 다음과 같은 단계로 이루어집니다.
- 초기 데이터 수집: 원시 목적함수 \(f\)를 몇몇 입력값 \(x\)에 대해 평가하여 데이터를 수집합니다.
- 서로게이트 모델 학습: 수집된 데이터를 사용하여 서로게이트 모델 \(S\)를 학습합니다.
- 최적화 실행: 학습된 서로게이트 모델을 사용하여 최적의 \(x\)를 찾습니다.
- 업데이트 및 반복: 새로운 \(x\)에서 원시 목적함수를 평가하고, 이 데이터로 서로게이트 모델을 업데이트한 후, 필요에 따라 반복합니다.
일반적인 예시: 공학 설계 최적화
공학 설계에서 복잡한 시뮬레이션을 통해 설계를 최적화하는 경우, 각 시뮬레이션 실행이 많은 시간과 비용을 필요로 합니다. 예를 들어, 항공기의 날개 설계를 최적화하는 경우, 다음과 같이 서로게이트 최적화를 적용할 수 있습니다.
- 초기 설계 평가: 몇 가지 초기 설계에 대해 공기역학 시뮬레이션을 수행합니다.
- 서로게이트 모델 구축: 이 데이터를 사용해 서로게이트 모델을 구축합니다. 가우시안 프로세스는 입력 설계와 출력 결과(e.g., 항력 계수) 사이의 관계를 모델링하는 데 자주 사용됩니다.
- 최적화 수행: 서로게이트 모델을 사용하여 최소 항력을 갖는 설계를 예측합니다.
- 실제 시뮬레이션 검증: 최적으로 예측된 설계를 실제 시뮬레이션으로 검증하고, 필요한 경우 과정을 반복합니다.
서로게이트 최적화는 실제 함수 평가를 최소화하면서도, 효과적인 최적화 결과를 도출할 수 있습니다.
[참고자료 2] Surrogate-base Optimization in DL, ML
AI에서의 서로게이트 최적화의 주요 고려사항
- (샘플 포인트 선택) 최적화의 효율성과 정확성을 높이기 위해 어떻게 샘플 포인트를 선택할지가 중요합니다.
- (서로게이트 모델 구축) 샘플 데이터를 사용하여 서로게이트 모델을 어떻게 구축할지 결정합니다.
- (모델 정확도 평가) 구축된 서로게이트 모델의 정확도를 어떻게 평가할지가 중요합니다.
서로게이트 최적화의 절차
서로게이트 최적화의 일반적인 절차는 다음과 같습니다.
- (데이터 수집) 탐색 가능한 공간에서 무작위 포인트를 샘플링하여 원시 목적함수를 평가합니다.
- (모델 학습) 수집된 데이터를 사용하여 서로게이트 모델을 학습합니다.
- (최적화 수행) 학습된 모델을 기반으로 최적의 솔루션을 찾습니다.
- (모델 업데이트 및 반복) 새로운 최적의 솔루션에서 원시 목적함수를 평가하고 결과를 사용하여 모델을 업데이트한 후 필요한 경우 이 과정을 반복합니다.
서로게이트 최적화의 실제 예시
서로게이트 모델링 기법
- 다항식 서페이스: 일반적으로 3차 다항식 서페이스를 사용하여 기존 데이터에 기반한 함수 \(f\)를 근사화합니다.
- 회귀 모델: 어떤 회귀 모델도 사용될 수 있으며,
fit과predict메소드를 구현해야 합니다.
최적화 알고리즘
- SciPy 최적화: SciPy의 최적화 도구를 사용하여 각 반복에서 서로게이트의 최소값을 찾습니다.
- 대안 최적화 도구:
Optimithon과 같은 대안적 최적화 도구를 사용할 수 있습니다.
샘플링 방법
- CompactSample: 가능한 집합에서 무작위 포인트를 샘플링합니다.
- BoxSample: 주어진 점 주위의 정육면체에서 샘플링합니다.
- SphereSample: 주어진 점을 중심으로 한 구에서 샘플링합니다.
서로게이트 최적화의 응용: 머신러닝의 하이퍼파라미터 최적화
머신러닝에서 하이퍼파라미터 최적화는 서로게이트 최적화 기법으로 효율적으로 수행될 수 있는데 예를 들어, 큰 모델(LLM 등)의 하이퍼파라미터 서치에서 비용과 시간을 절약하면서 최적의 하이퍼파라미터를 찾을 수 있습니다.
SKSurrogate와 SVC를 사용한 예제
다음과 같이 서로게이트 베이스 최적화를 사용할 경우, SVC 분류기의 최적 하이퍼파라미터를 탐색하는 전통적인 GridSearchCV나 RandomizedSearchCV보다 훨씬 비용 효율적으로 탐색할 수 있다는 장점이 있습니다.
from sklearn.svm import SVC
from SKSurrogate import SurrogateRandomCV
# SVC 분류기 설정
clf = SVC()
params = {
'C': Real(1.e-5, 10),
'kernel': Categorical(['poly', 'rbf']),
'degree': Integer(1, 4),
'gamma': Real(1.e-5, 10),
'class_weight': HDReal((1.e-3, 1.e-3), (10., 10.))
}
# 서로게이트 기반 하이퍼파라미터 최적화 실행
srch = SurrogateRandomCV(clf, params)
srch.fit(X, y)
print(srch.best_estimator_)
1 Introduction
In recent years, several different approaches have been proposed for reinforcement learning with neural network function approximators. The leading contenders are deep Q-learning [Mni+15], “vanilla” policy gradient methods [Mni+16], and trust region/natural policy gradient methods [Sch+15b]. However, there is room for improvement in developing a method that is scalable (to large models and parallel implementations), data efficient, and robust (i.e., successful on a variety of problems without hyperparameter tuning). Q-learning (with function approximation) fails on many simple problems and is poorly understood, vanilla policy gradient methods have poor data efficiency and robustness; and trust region policy optimization (TRPO) is relatively complicated, and is not compatible with architectures that include noise (such as dropout) or parameter sharing (between the policy and value function, or with auxiliary tasks). This paper seeks to improve the current state of affairs by introducing an algorithm that attains the data efficiency and reliable performance of TRPO, while using only first-order optimization. We propose a novel objective with clipped probability ratios, which forms a pessimistic estimate (i.e., lower bound) of the performance of the policy. To optimize policies, we alternate between sampling data from the policy and performing several epochs of optimization on the sampled data. Our experiments compare the performance of various different versions of the surrogate objective, and find that the version with the clipped probability ratios performs best. We also compare PPO to several previous algorithms from the literature. On continuous control tasks, it performs better than the algorithms we compare against. On Atari, it performs significantly better (in terms of sample complexity) than A2C and similarly to ACER though it is much simpler.
While DQN works well on game environments like the Arcade Learning Environment [Bel+15] with discrete action spaces, it has not been demonstrated to perform well on continuous control benchmarks such as those in OpenAI Gym [Bro+16] and described by Duan et al. [Dua+16].
2 Background: Policy Optimization
2.1 Policy Gradient Methods
Policy gradient methods work by computing an estimator of the policy gradient and plugging it into a stochastic gradient ascent algorithm. The most commonly used gradient estimator has the form:
\[\hat{g} = \hat{\mathbb{E}}[\nabla_{\theta} \log \pi_{\theta}(a_t\\|s_t) \hat{A}_t] \tag{1}\]where $\pi_{\theta}$ is a stochastic policy, and $\hat{A}_t$ is an estimator of the advantage function at time step $t$. Here, the expectation $\hat{\mathbb{E}}[\ldots]$ indicates the empirical average over a finite batch of samples, in an algorithm that alternates between sampling and optimization. Implementations that use automatic differentiation software work by constructing an objective function whose gradient is the policy gradient estimator; the estimator $\hat{g}$ is obtained by differentiating the objective:
\[\mathcal{L}_{\text{PG}}( heta) = \hat{\mathbb{E}}[\theta \log \pi_{\theta}(a_t\\|s_t) \hat{A}_t] \tag{2}\]While it is appealing to perform multiple steps of optimization on this loss $\mathcal{L}_{\text{PG}}$ using the same trajectory, doing so is not well-justified, and empirically it often leads to destructively large policy updates (see Section 6.1; results are not shown but were similar or worse than the “no clipping or penalty” setting).
2.2 Trust Region Methods
In TRPO [Sch+15b], an objective function (the “surrogate” objective) is maximized subject to a constraint on the size of the policy update. Specifically, maximize:
\[\theta \, \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t\\|s_t)}{\pi_{\theta_{\text{old}}}(a_t\\|s_t)} \hat{A}_t \right] \tag{3}\]subject to
\[\hat{\mathbb{E}} \left[ \text{KL}[\pi_{\theta_{\text{old}}}(\cdot\\|s_t), \pi_{\theta}(\cdot\\|s_t)] \right] \leq \delta \tag{4}\]Here, $\theta_{\text{old}}$ is the vector of policy parameters before the update. This problem can efficiently be approximately solved using the conjugate gradient algorithm, after making a linear approximation to the objective and a quadratic approximation to the constraint.
The theory justifying TRPO actually suggests using a penalty instead of a constraint, i.e., solving the unconstrained optimization problem:
\[\text{maximize} \, \theta \, \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t\\|s_t)}{\pi_{\theta_{\text{old}}}(a_t\\|s_t)} \hat{A}_t - \beta \text{KL}[\pi_{\theta_{\text{old}}}(\cdot\\|s_t), \pi_{\theta}(\cdot\\|s_t)] \right] \tag{5}\]for some coefficient $\beta$.
This follows from the fact that a certain surrogate objective (which computes the max KL over states instead of the mean) forms a lower bound (i.e., a pessimistic bound) on the performance of the policy $\pi$. TRPO uses a hard constraint rather than a penalty because it is hard to choose a single value of $\beta$ that performs well across different problems—or even within a single problem, where the characteristics change over the course of learning. Hence, to achieve our goal of a first-order algorithm that emulates the monotonic improvement of TRPO, experiments show that it is not sufficient to simply choose a fixed penalty coefficient $\beta$ and optimize the penalized objective in Equation (5) with SGD; additional modifications are required.
3 Clipped Surrogate Objective
[Overview]
Epsilon Hyperparameter:
Let \(\epsilon = 0.2\).
Objective Motivation:
The first term inside the min is LCPI. The second term, \(\text{clip}(r_t( heta), 1-\epsilon, 1+\epsilon) \hat{A}_t\), modifies the surrogate objective by clipping the probability ratio, which removes the incentive for moving \(r_t\) outside of the interval \([1-\epsilon, 1+\epsilon]\). We take the minimum of the clipped and unclipped objective, so the final objective is a lower bound (i.e., a pessimistic bound) on the unclipped objective. This ensures we only ignore the change in probability ratio when it would improve the objective and include it when it makes the objective worse.
Details on LCLIP:
- \(L_{\text{CLIP}}( heta) = L_{\text{CPI}}( heta)\) to first order around \(\theta_{\text{old}}\) (i.e., where \(r = 1\)), but they differ as \(\theta\) moves away from \(\theta_{\text{old}}\).
[Body]
Let $ r_t( heta) $ denote the probability ratio:
\[r_t( heta) = \frac{\pi_{\theta}(a_t\\|s_t)}{\pi_{\theta_{\text{old}}}(a_t\\|s_t)}\]so $ r( heta_{\text{old}}) = 1 $.
TRPO maximizes a “surrogate” objective:
\[\mathcal{L}_{\text{CPI}}( heta) = \hat{\mathbb{E}} \left[ \frac{\pi_{\theta}(a_t\\|s_t)}{\pi_{\theta_{\text{old}}}(a_t\\|s_t)} \hat{A}_t \right] \tag{6}\]The superscript CPI refers to conservative policy iteration [KL02], where this objective was proposed. Without a constraint, maximization of $\mathcal{L}_{\text{CPI}}$ would lead to an excessively large policy update; hence, we now consider how to modify the objective to penalize changes to the policy that move $ r( heta) $ away from 1.
The main objective we propose is the following:
\[\mathcal{L}_{\text{CLIP}}( heta) = \hat{\mathbb{E}} \left[ \min \left( r_t( heta) \hat{A}_t, \, \text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] \tag{7}\]where $\epsilon$ is a hyperparameter, say, $\epsilon = 0.2$. The motivation for this objective is as follows.
The first term inside the min is \(\mathcal{L}_{\text{CPI}}\). The second term, \(\text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t\), modifies the surrogate objective by clipping the probability ratio, which removes the incentive for moving $ r_t $ outside of the interval \([1 - \epsilon, 1 + \epsilon]\). Finally, we take the minimum of the clipped and unclipped objective, so the final objective is a lower bound (i.e., a pessimistic bound) on the unclipped objective. With this scheme, we only ignore the change in probability ratio when it would make the objective improve, and we include it when it makes the objective worse. Note that \(\mathcal{L}_{\text{CLIP}}( heta) = \mathcal{L}_{\text{CPI}}( heta)\) to the first order around \(\theta_{\text{old}}\) (i.e., where \(r = 1\)), however, they become different as $\theta$ moves away from $\theta_{\text{old}}$.
Figure 1 plots a single term (i.e., a single time step) of the surrogate function $Lclip$ as a function of the probability ratio r, for positive advantages (left) and negative advantages (right). The red circle on each plot shows the starting point for the optimization, i.e., $r$ = 1. Note that $Lclip$ sums many of these terms.
4. Adaptive KL Penalty Coefficient
[Overview]
Alternative Approach: Used either in addition to or as an alternative to the clipped surrogate objective, this approach involves a penalty on KL divergence, adapting the penalty coefficient to achieve some target value of the KL divergence each policy update.
Steps Include:
- Optimize the KL-penalized objective \(L_{\text{KL-PEN}}( heta)\).
- Adjust \(\beta\) based on the difference from the target KL divergence.
Equations:
\[L_{\text{KL-PEN}}( heta) = \hat{E}_t \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)} \right] - \beta \text{KL}[\pi_{\theta_{\text{old}}}(\cdot | s_t), \pi_{\theta}(\cdot | s_t)]\]- If \(d < \frac{\text{d}_{\text{targ}}}{1.5}\), then \(\beta \leftarrow \frac{\beta}{2}\)
- If \(d > 1.5 \times \text{d}_{\text{targ}}\), then \(\beta \leftarrow 2 \times \beta\)
[Body]
Another approach, which can be used as an alternative to the clipped surrogate objective or in addition to it, is to use a penalty on KL divergence, and to adapt the penalty coefficient so that we achieve some target value of the KL divergence \(d_{\text{targ}}\) each policy update. In our experiments, we found that the KL penalty performed worse than the clipped surrogate objective, however, we’ve included it here because it’s an important baseline.
In the simplest instantiation of this algorithm, we perform the following steps in each policy update:
- Using several epochs of minibatch SGD, optimize the KL-penalized objective \(L_{\text{KLPEN}}( heta)\).
- Compute \(d = \hat{E}_t[\text{KL}[\pi_{\theta_{\text{old}}}(\cdot \\| s_t), \pi_{\theta}(\cdot \\| s_t)]]\).
- If \(d < d_{\text{targ}}/1.5\), \(\beta \leftarrow \beta/2\)
- If \(d > d_{\text{targ}} \times 1.5\), \(\beta \leftarrow \beta \times 2\)
The updated \(\beta\) is used for the next policy update. With this scheme, we occasionally see policy updates where the KL divergence is significantly different from \(d_{\text{targ}}\), however, these are rare, and \(\beta\) quickly adjusts. The parameters 1.5 and 2 above are chosen heuristically, but the algorithm is not very sensitive to them. The initial value of \(\beta\) is another hyperparameter but is not important in practice because the algorithm quickly adjusts it.
5. Algorithm
The surrogate losses from the previous sections can be computed and differentiated with a minor change to a typical policy gradient implementation. For implementations that use automatic differentiation, one simply constructs the loss \(L_{\text{CLIP}}\) or \(L_{\text{KLPEN}}\) instead of \(L_{\text{PG}}\), and one performs multiple steps of stochastic gradient ascent on this objective.
Most techniques for computing variance-reduced advantage-function estimators make use of a learned state-value function \(V(s)\); for example, generalized advantage estimation, or the finite-horizon estimators in past research. If using a neural network architecture that shares parameters between the policy and value function, we must use a loss function that combines the policy surrogate and a value function error term. This objective can further be augmented by adding an entropy bonus to ensure sufficient exploration, as suggested in past work.
Combining these terms, we obtain the following objective, which is (approximately) maximized each iteration:
\[L_{\text{CLIP+VF+S}}( heta) = \hat{E}_t[L_{\text{CLIP}}( heta) - c_1 L_{\text{VF}}( heta) + c_2 S[\pi_{\theta}](s_t)],\]where \(c_1, c_2\) are coefficients, and \(S\) denotes an entropy bonus, and
The loss function \(L_{\text{VF}}( heta)\) is defined as a squared-error loss:
\[L_{\text{VF}}( heta) = (V_{\theta}(s_t) - V_{\text{targ}}(s_t))^2 \tag{9}\]One style of policy gradient implementation, popularized in recent studies and well-suited for use with recurrent neural networks, runs the policy for \(T\) timesteps (where \(T\) is much less than the episode length), and uses the collected samples for an update. This style requires an advantage estimator that does not look beyond timestep \(T\). The estimator used is:
\[\hat{A}_t = -V(s_t) + r_t + \gamma r_{t+1} + \ldots + \gamma^{T-t+1} r_{T-1} + \gamma^{T-t} V(s_T) \tag{10}\]where \(t\) specifies the time index in \([0,T]\), within a given length-\(T\) trajectory segment. Generalizing this choice, we can use a truncated version of generalized advantage estimation, which reduces to Equation (10) when \(\lambda = 1\):
The advantage estimator \(\hat{A}_t\) is expressed as:
\[\hat{A}_t = \delta_t + (\gamma \lambda) \delta_{t+1} + \cdots + (\gamma \lambda)^{T-t+1} \delta_{T-1} \tag{11}\]where \(\delta_t\) is defined as:
\[\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t) \tag{12}\]A proximal policy optimization (PPO) algorithm that uses fixed-length trajectory segments is shown below. Each iteration, each of \(N\) (parallel) actors collect \(T\) timesteps of data. Then we construct the surrogate loss on these \(NT\) timesteps of data, and optimize it with minibatch SGD (or usually for better performance, Adam), for \(K\) epochs.
PPO, Actor-Critic Style
\[\begin{align*} \text{for iteration} &= 1,2,\ldots \text{ do} \\ \text{for actor} &= 1,2,\ldots,N \text{ do} \\ &\text{Run policy } \pi_{\theta_{\text{old}}} \text{ in environment for } T \text{ timesteps} \\ &\text{Compute advantage estimates } \hat{A}_1, \ldots, \hat{A}_T \\ \text{end for} \\ &\text{Optimize surrogate } L \text{ wrt } \theta, \text{ with } K \text{ epochs and minibatch size } M \leq NT \\ &\theta_{\text{old}} \leftarrow \theta \\ \text{end for} \end{align*}\]Implementation Details
- Algorithm 1: PPO
- For iteration=1,2,… do:
- For actor=1,2,…,N do:
- Run policy \(\pi_{\theta_{\text{old}}}\) in environment for \(T\) timesteps.
- Compute advantage estimates \(\hat{A}_1, ..., \hat{A}_T\).
- Optimize surrogate \(L\) with respect to \(\theta\), using minibatch SGD.
- For actor=1,2,…,N do:
- For iteration=1,2,… do:
6. Experiments
6.1 Comparison of Surrogate Objectives
First, we compare several different surrogate objectives under different hyperparameters. Here, we compare the surrogate objective LCLIP to several natural variations and ablated versions:
- No clipping or penalty: \(L_t( heta) = r_t( heta) \hat{A}_t\)
- Clipping: \(L_t( heta) = \min(r_t( heta) \hat{A}_t, \text{clip}(r_t( heta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t)\)
- KL penalty (fixed or adaptive): \(L_t( heta) = r_t( heta) \hat{A}_t - \beta \text{KL}[\pi_{\theta_{\text{old}}}, \pi_{\theta}] \hat{A}_t\)
For the KL penalty, one can either use a fixed penalty coefficient \(\beta\) or an adaptive coefficient as described in Section 4 using target KL value \(d_{\text{targ}}\). Note that we also tried clipping in log space, but found the performance to be no better.
Because we are searching over hyperparameters for each algorithm variant, we chose a computationally cheap benchmark to test the algorithms on. Namely, we used 7 simulated robotics tasks implemented in OpenAI Gym, which use the MuJoCo physics engine. We do one million timesteps of training on each one. Besides the hyperparameters used for clipping (\(\epsilon\)) and the KL penalty (\(\beta, d_{\text{targ}}\)), the other hyperparameters are provided in Table 3. To represent the policy, we used a fully-connected MLP with two hidden layers of 64 units, and tanh nonlinearities, outputting the mean of a Gaussian distribution, with variable standard deviations. We don’t share parameters between the policy and value function (so coefficient \(c1\) is irrelevant), and we don’t use an entropy bonus. Each algorithm was run on all 7 environments, with 3 random seeds on each. We scored each run of the algorithm by computing the average total reward of the last 100 episodes. We shifted and scaled the scores for each environment so that the random policy gave a score of 0 and the best result was set to 1, and averaged over 21 runs to produce a single scalar for each algorithm setting.
Table 1: Results from Continuous Control Benchmark
Average normalized scores (over 21 runs of the algorithm, on 7 environments) for each algorithm / hyperparameter setting.
| Algorithm Setting | Avg. Normalized Score |
|---|---|
| No clipping or penalty | -0.39 |
| Clipping, \(\epsilon = 0.1\) | 0.76 |
| Clipping, \(\epsilon = 0.2\) | 0.82 |
| Clipping, \(\epsilon = 0.3\) | 0.70 |
| Adaptive KL \(d_{\text{targ}} = 0.003\) | 0.68 |
| Adaptive KL \(d_{\text{targ}} = 0.01\) | 0.74 |
| Adaptive KL \(d_{\text{targ}} = 0.03\) | 0.71 |
| Fixed KL, \(\beta = 0.3\) | 0.62 |
| Fixed KL, \(\beta = 1\) | 0.71 |
| Fixed KL, \(\beta = 3\) | 0.72 |
| Fixed KL, \(\beta = 10\) | 0.69 |
6.2 Comparison to Other Algorithms in the Continuous Domain
Next, we compare PPO (with the “clipped” surrogate objective from Section 3) to several other methods from the literature, which are considered to be effective for continuous problems. We compared against tuned implementations of the following algorithms: trust region policy optimization, cross-entropy method (CEM), vanilla policy gradient with adaptive stepsize, and A2C with trust region. For PPO, we used the hyperparameters from the previous section, with \(\epsilon = 0.2\). We see that PPO outperforms the previous methods on almost all the continuous control environments.
6.3 Showcase in the Continuous Domain: Humanoid Running and Steering
To showcase the performance of PPO on high-dimensional continuous control problems, we train on a set of problems involving a 3D humanoid, where the robot must run, steer, and get up off the ground, possibly while being pelted by cubes. The tasks we test on are:
- RoboschoolHumanoid: forward locomotion only.
- RoboschoolHumanoidFlagrun: position of target is randomly varied every 200 timesteps or whenever the goal is reached.
- RoboschoolHumanoidFlagrunHarder: where the robot is pelted by cubes and needs to get up off the ground.
6.4 Comparison to Other Algorithms on the Atari Domain
We also ran PPO on the Arcade Learning Environment benchmark and compared against well-tuned implementations of A2C and ACER. For all three algorithms, we used the same policy network architecture as used previously. The hyperparameters for PPO are provided in Table 5. For the other two algorithms, we used hyperparameters that were tuned to maximize performance on this benchmark. A table of results and learning curves for all 49 games is provided in Appendix B. We consider the following two scoring metrics:
- Average reward per episode over the entire training period (which favors fast learning).
- Average reward per episode over the last 100 episodes of training (which favors final performance).
| Algorithm | Avg. Reward Over All Training | Avg. Reward Over Last 100 Episodes |
|---|---|---|
| A2C | 1 | 28 |
| ACER | 1 | 30 |
| PPO | 18 | 19 |
| Tie | 0 | 1 |
Table 2: Number of Games “Won” by Each Algorithm
Where the scoring metric is averaged across three trials.
This structured approach provides clarity and detailed insights into the experiments and comparisons discussed in the original content.
Comparative Study:
- Various surrogate objectives tested under different hyperparameters.
- PPO demonstrated superior performance across several continuous control environments.
- Figure 2 & 3: Illustrate performance metrics and learning curves.
7. Conclusion
We introduced Proximal Policy Optimization (PPO), a method that combines the stability and reliability of trust-region methods with simplicity, applicable in general settings, and improved performance. This approach requires minor code changes to a typical policy gradient implementation.