Prover Model | DeepSeek-Prover-V1.5

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-15

DeepSeek-Prover-V1.5: Harnessing Proof Assistant Feedback for Reinforcement Learning and Monte-Carlo Tree Search

• url: https://arxiv.org/abs/2408.08152
• pdf: https://arxiv.org/pdf/2408.08152
• html: https://arxiv.org/html/2408.08152v1
• abstract: We introduce DeepSeek-Prover-V1.5, an open-source language model designed for theorem proving in Lean 4, which enhances DeepSeek-Prover-V1 by optimizing both training and inference processes. Pre-trained on DeepSeekMath-Base with specialization in formal mathematical languages, the model undergoes supervised fine-tuning using an enhanced formal theorem proving dataset derived from DeepSeek-Prover-V1. Further refinement is achieved through reinforcement learning from proof assistant feedback (RLPAF). Beyond the single-pass whole-proof generation approach of DeepSeek-Prover-V1, we propose RMaxTS, a variant of Monte-Carlo tree search that employs an intrinsic-reward-driven exploration strategy to generate diverse proof paths. DeepSeek-Prover-V1.5 demonstrates significant improvements over DeepSeek-Prover-V1, achieving new state-of-the-art results on the test set of the high school level miniF2F benchmark (63.5%) and the undergraduate level ProofNet benchmark (25.3%).

TL;DR

1. DeepSeek-Prover-V1.5는 전체 증명 생성과 몬테 카를로 트리 검색을 활용하여 높은 성능을 달성하였고, MCTS를 활용한 접근 방식은 증명 과정에서 다양한 가능성을 탐색할 수 있도록 하여, 더 많은 증명을 성공적으로 완료할 수 있었다고 보고합니다.
2. 온라인 강화 학습(RL)을 통해 모델의 성능을 향상시킨 결과 DeepSeek-Prover-V1.5는 기존 모델들을 뛰어넘는 증명 성공률을 보여, 강화 학습이 복잡한 증명 과제에서도 효과적으로 작용할 수 있음을 보여줍니다.
3. 증명 과정을 트리 구조로 분해하고 이를 통해 증명을 단계적으로 생성하는 방식은 전체 증명 생성에 비해 더 높은 정확도를 달성합니다. 트리 구조로 분해 및 단계적 생성하는 방법은 증명 과정 중 발생할 수 있는 오류를 줄이고, 각 단계에서의 검증을 통해 최종적으로 정확한 증명을 도출할 수 있게 한다고 언급합니다.

핵심 방법

1. 몬테 카를로 트리 검색 (MCTS): 증명 과정을 트리 구조로 추상화하여, 다양한 증명 경로를 탐색하고 평가함으로써 가장 유효한 증명 방법을 도출해 증명 과정의 다양성을 확보하고 성공률을 높이도록 하였습니다.
2. 강화 학습 (RL): 모델이 실제 증명 과정에서 얻은 피드백을 기반으로 학습하여, 증명의 정확성과 효율성을 개선하여 모델이 더 정확한 증명을 생성하도록 합니다.
3. 전술적 트리 추상화와 재개 기법 (Truncate-and-Resume): 증명을 트리 노드로 분해하고, 오류가 발견되면 재개점을 정하여 증명을 계속 진행해 오류를 빠르게 수정하고, 증명 과정을 정확하게 유지하는 데 도움을 줍니다.
4. 보상 없는 탐색 알고리즘 (RMaxTS): 새로운 증명 노드를 추가할 때 마다 최대 보상을 자체적으로 부여함으로써, 탐색 과정에서의 다양한 증명 경로를 촉진해 보상이 희박한 증명 검색 문제에서 효과적인 탐색 전략을 제공합니다.

1. 서론

최근 대규모 언어모델은 수학적 인퍼런스 및 이론 증명 분야에 상당한 영향을 미치고 있습니다. 특히, Lean 4와 Isabelle과 같은 형식적 증명 시스템에서의 과제는 코드 및 수학적 복잡성의 이해를 필요로 합니다. 전통적인 언어 모델이 자연어 처리에서 성과를 보이고 있지만, 형식적 증명의 정밀성은 더 큰 챌린지를 제시합니다. 이런 배경에서, DeepSeek-Prover-V1.5는 전체 증명과 단계별 증명 생성 방식을 통합하여 효율성과 정확성을 동시에 추구합니다.

DeepSeek-Prover-V1.5의 설계 및 개선

기존 모델과의 비교

DeepSeek-Prover-V1.5는 전체 증명 생성과 단계별 증명 생성의 장점을 결합한 새로운 접근 방식을 제시합니다. 초기에는 전체 증명 코드를 생성하고, 오류가 감지되면 첫 번째 오류 지점에서 코드를 잘라내고 새로운 증명 단계를 생성합니다. 이는 Lean 검증기의 피드백을 반영하여, 모델이 새로운 증명을 생성할 때 가장 높은 검증 상태를 반영하도록 합니다.

Monte-Carlo 트리 탐색(MCTS)

MCTS는 증명 과정에서 여러 가능성을 탐색할 수 있는 알고리즘으로, RMaxTS 전략을 도입하여 탐색 과정에서 내재된 보상 시스템을 활용합니다. 이는 탐색 과정에서 다양한 증명 경로를 생성하도록 유도하여, 모델이 더 넓은 범위의 증명 가능성을 탐색하도록 합니다.

데이터셋 및 벤치마크

DeepSeek-Prover-V1.5는 miniF2F와 ProofNet 벤치마크를 사용하여, 학교 수준에서부터 대학 수준까지 다양한 복잡성의 이론을 증명하는 데 사용됩니다. 각각의 벤치마크에 대해 향상된 상태를 달성하였으며, 이는 이전 모델 대비 큰 향상을 의미합니다.

수학적 정리 증명에서 중요한 것은 증명의 각 단계가 논리적으로 연결되어야 한다는 점입니다. 예를 들어, $ a^2 + b^2 = c^2 $에서 $ a $, $ b $, $ c $가 각각 삼각형의 변을 나타내는 경우, 이는 피타고라스의 정리를 사용하여 증명할 수 있습니다. DeepSeek-Prover-V1.5는 이런 수학적 구조를 이해하고, 다음과 같이 정리를 증명합니다.

2. 모델 훈련

2.1 사전 학습 (Pre-training)

DeepSeek-Prover-V1.5의 기반 모델은 Lean, Isabelle, Metamath와 같은 형식적 언어에 초점을 맞추어 고품질 데이터셋에서 추가 학습을 받았습니다. 이를 통해 모델은 형식적 수학 언어에서의 증명 생성에 능숙해졌습니다.

2.2 Supervised learning (Supervised Fine-tuning)

DeepSeek-Prover-V1로부터 확장된 증명 데이터셋을 이용하여 DeepSeek-Prover-V1.5 모델을 파인튜닝하였습니다. 이 과정에서 자연어 설명과 Lean 4 코드 간의 연계를 강화하는 데 중점을 두었습니다. 또한, Monte-Carlo 트리 검색 과정에 사용될 ‘truncate-and-resume’ 메커니즘을 지원하기 위해 중간 전술 상태 정보를 추가하였습니다.

2.3 강화 학습 (Reinforcement Learning from Proof Assistant Feedback)

DeepSeek-Prover-V1.5-RL 모델은 Lean 4 검증기로부터의 피드백을 바탕으로 성능을 향상시키기 위해 강화 학습을 도입하였습니다. 이 단계에서는 실제 증명 검증 결과를 바탕으로 이루어진 보상을 통해 모델이 향상됩니다.

2.4 평가 (Evaluation)

모델의 평가는 두 가지 벤치마크, miniF2F와 ProofNet을 사용하여 수행되었습니다. 이 두 벤치마크는 각각 고등학교 수준과 대학 수준의 수학 증명 능력을 평가합니다. 평가 결과, 각 단계의 훈련을 거치며 모델의 증명 성공률이 지속적으로 향상되었습니다.

피타고라스 정리 예시

피타고라스 정리는 증명의 예로 자주 사용됩니다. 모델이 적용한 논리적 접근 방식을 수학적 표현으로 설명하면 다음과 같습니다.

이와 같은 단계별 접근 방식은 모델이 각 증명 과정에서 어떻게 논리적 결론에 도달하는지를 보여줍니다. 모든 단계는 각각의 전술과 그 결과를 명확하게 연결하여, 복잡한 수학적 목표를 해결하는 데 필요한 구조적 인퍼런스를 가능하게 합니다.

DeepSeek-Prover-V1.5는 이런 방법을 통해 더 높은 정확성과 다양한 증명 경로 생성 능력을 보여주며, 특히 복잡한 형식적 증명 과제에서 그 성능을 입증하였습니다.

3. 탐색 지향 몬테카를로 트리 검색

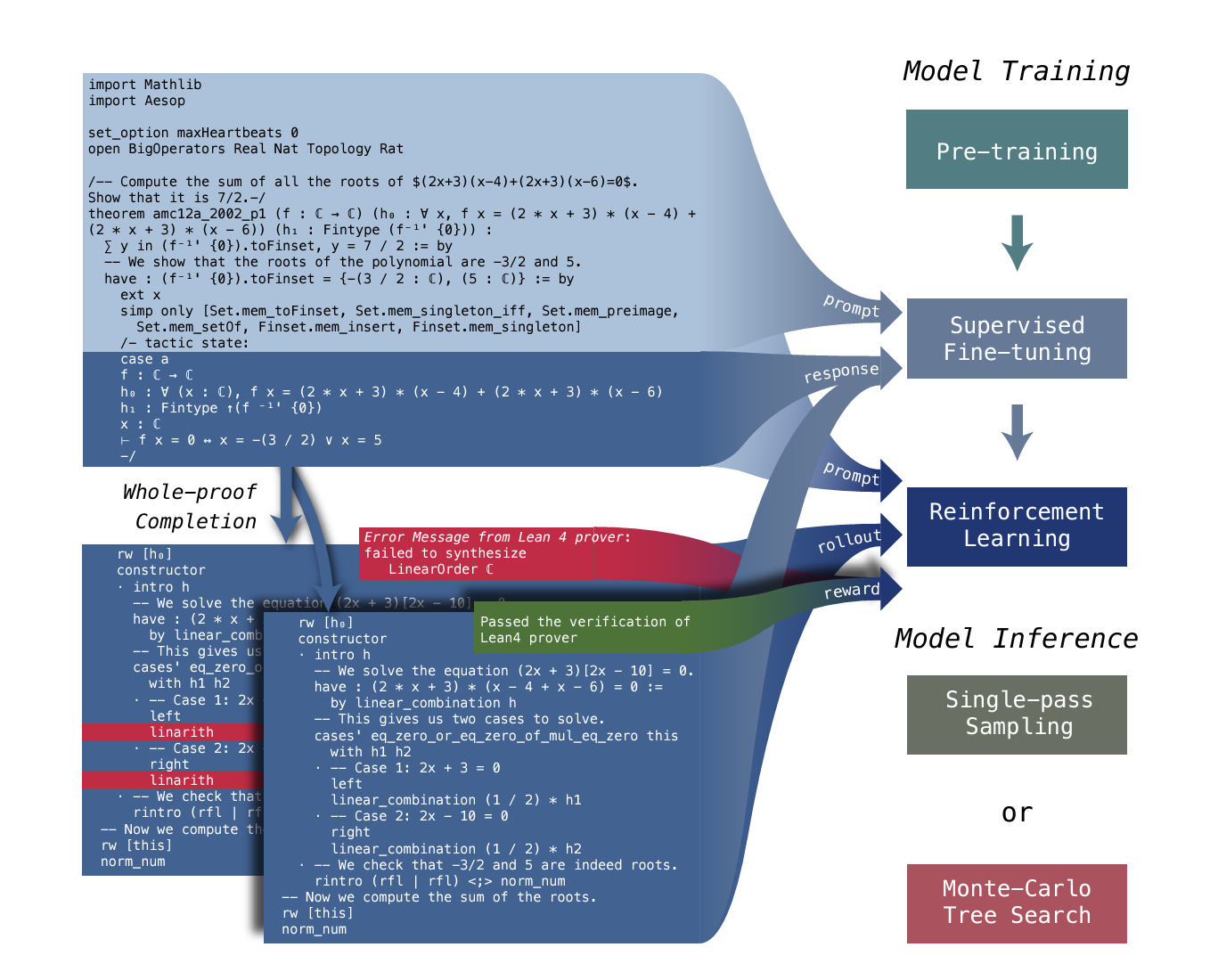
Figure 2. Overall Framework.

DeepSeek-Prover-V1.5 is trained through pre-training, supervised fine-tuning, and reinforcement learning. During supervised fine-tuning, the pre-trained model receives an incomplete theorem proof ending with a tactic state comment keyword. The model is trained to predict the content of this tactic state (auxiliary objective) and complete the subsequent proof steps (main objective). In the reinforcement learning stage, given an incomplete theorem proof and ground-truth tactic state from the Lean prover, we roll out the f ine-tuned model to generate multiple proof candidates, which are then verified by the Lean prover. The verification results for these candidates are used as binary (0-1) rewards to further optimize the model and enhance its alignment with the formal specifications of the verification system. For model inference, we offer two alternatives: single-pass sampling and Monte-Carlo tree search.

DeepSeek-Prover-V1.5는 사전 훈련, 감독된 파인튜닝, 강화 학습을 통해 훈련됩니다. 감독된 파인튜닝 동안, 사전 훈련된 모델은 불완전한 정리 증명을 받고 택틱 상태 주석 키워드로 끝납니다. 이 모델은 이 택틱 상태의 내용을 예측하고 후속 증명 단계를 완성하도록 훈련됩니다(보조 목표). 강화 학습 단계에서는 불완전한 정리 증명과 Lean 증명기의 ground-truth 택틱 상태를 주어진 상태에서 파인튜닝된 모델을 사용하여 여러 증명 후보를 생성하며, 이후 Lean 증명기에 의해 검증됩니다. 이 후보들의 검증 결과는 이진(0-1) 보상으로 사용되어 모델을 추가로 최적화하고 검증 시스템의 공식 사양과의 일치를 강화합니다. 모델 인퍼런스를 위해 단일 통과 샘플링과 몬테카를로 트리 검색의 두 가지 대안을 제공합니다.

탐색 기반 몬테카를로 트리 검색을 이용한 증명 전략

• 전략적 트리 추상화: 증명 과정을 트리 구조로 분해하여 탐색
• 몬테카를로 트리 검색: 선택, 확장, 시뮬레이션, 역전파 단계를 반복
• 병렬 처리 기술: 효율적인 탐색을 위해 병렬 처리 기술 적용

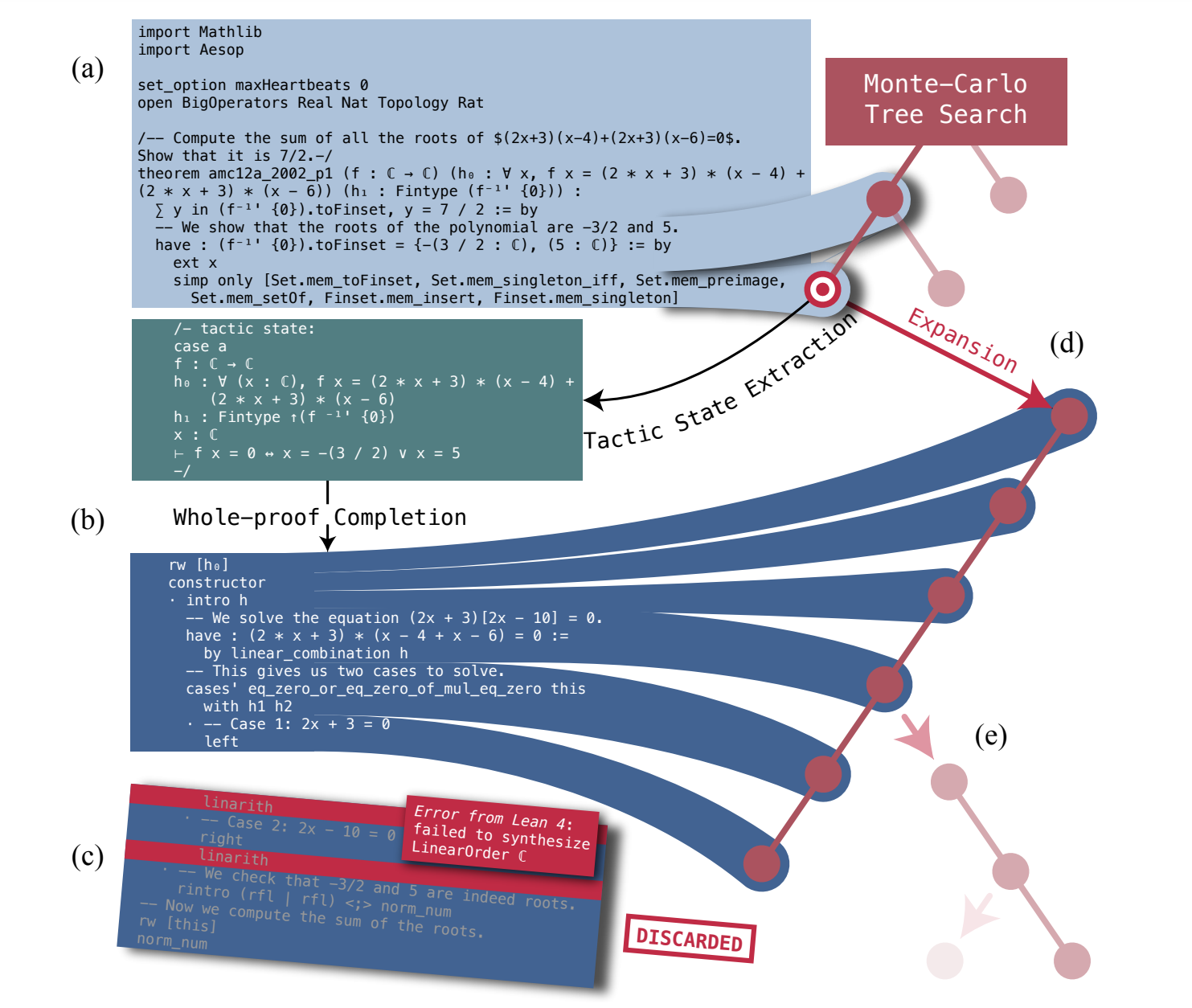
Figure 4. Truncate-and-Resume Mechanism in the Expansion Step of MCTS.

• (a) 노드 선택 및 증명 코드 추적: 노드를 선택한 후, 해당 노드의 불완전한 증명 코드 접두부(파일 헤더, 초기 명령문, 상위 노드에서 성공적으로 적용된 전술 포함)를 추적. After selecting a node, we trace its corresponding incomplete proof code prefix, which includes the file header, initial statement, and successfully applied tactics from the ancestor nodes.
• (b) 언어 모델을 통한 증명 생성: 언어 모델이 이 접두부와 현재 전술 상태를 설명하는 주석 블록을 기반으로 후속 증명 코드를 생성. The language model then generates the subsequent proof based on this prefix along with a comment block containing the current tactic state.
• (c) 코드 검증: 생성된 증명 코드(접두부와 새로 생성된 코드 결합)는 Lean 4 증명기에 의해 검증되며, 오류가 없으면 트리 탐색을 종료. The combined proof code (prefix and newly generated code) is verified by the Lean 4 prover. If no errors are found, the tree-search procedure terminates. If errors are detected, we truncate the newly generated code at the first error message, discard the subsequent code, and parse the successful portion into tactics.
• (d) 오류 발생 시 코드 절단: 오류가 발견되면, 첫 번째 오류 메시지에서 새로 생성된 코드를 절단하고, 성공적으로 실행된 부분만 전술로 파싱하여 트리의 새로운 노드로 추가. Each tactic is added as a new node in the search tree, extending a chain of descendants beneath the selected node.
• (e) 트리 업데이트 및 반복: 트리 업데이트가 완료되면, 다음 확장 단계에서 대체 후보 노드를 선택하여 반복적으로 과정으로 올바른 증명이 발견되거나 샘플 예산이 소진될 때까지 반복. Once the tree updates are complete, the next iteration of expansion begins by selecting an alternative candidate node, which is not limited to leaf nodes. This process repeats until a correct proof is found or the sample budget is exhausted.

3.1 전술 수준의 트리 추상화

1. 불완전한 증명을 개별 증명 단계에 해당하는 트리 노드 시퀀스로 분해
2. 이 트리 노드에 저장된 부분 내용을 사용하여 증명 생성 과정을 계속
3. 전술 수준에서 증명 탐색 트리를 구성하며, 각 트리 엣지는 전술 상태의 단일 전이 단계를 나타냄.
4. 생성된 전체 증명을 Lean 증명기에 제출하여 전술로 파싱
5. 가장 빠른 검증 오류에서 증명을 잘라내어, 후속 전술 코드가 원하는 정리를 향해 증명을 진전시킬 수 있도록 수정

전체 증명 생성 설정에서 트리 검색 방법을 구현하기 위해, 증명 트리 추상화를 도입하여 맞춤형 상태와 행동 공간을 정의합니다. 이 방법은 Yao et al. (2023, ReAct, 본 논문은 Tree of Thought)의 패러다임을 따라 불완전한 증명을 개별 증명 단계에 해당하는 일련의 트리 노드로 분해하고, 이 트리 노드에 저장된 부분적인 내용을 사용하여 증명 생성 과정을 계속합니다.

• Truncate(축소): 증명을 트리 노드로 분해합니다. 각 트리 가장자리는 전술 상태의 단일 전환 단계를 나타냅니다. 먼저 모델이 생성한 전체 증명을 Lean 증명기에 제출하여 전술로 구문 분석합니다. 그런 다음 가장 먼저 발생하는 검증 오류에서 증명을 축소하여 모든 후속 전술 코드가 원하는 정리로 증명을 진행할 수 있도록 합니다. 각 전술 코드는 유효한 전술 코드와 관련 사고 과정 코멘트를 포함한 여러 코드 분할로 세분화됩니다.
• Resume(재개): 트리 노드에서 증명 생성을 재개합니다. Lean 4에서 다른 전술이 같은 전술 상태로 이어질 수 있으므로, 각 노드는 동일한 결과를 달성할 수 있는 다양한 전술 코드에 해당할 수 있습니다. 트리 검색 에이전트가 노드를 확장할 때, 랜덤으로 하나의 전술을 선택하여 언어 모델의 프롬프트로 사용합니다.

3.2 몬테카를로 트리 검색을 통한 상호작용적 정리 증명

표준 몬테카를로 트리 검색(MCTS) 패러다임을 사용하여 증명 검색 트리를 개발합니다. 이는 선택(Selection), 확장(Expansion), 시뮬레이션(Simulation), 및 역전파(Backpropagation)의 네 단계를 반복적으로 적용합니다.

• Selection(선택): 선택 단계는 루트 노드에서 시작하여 확장할 유망한 노드를 식별하기 위해 아래로 이동합니다. 트리 노드 \(s\)에서 트리 정책은 유효한 작업 집합에서 가치를 최대화하는 행동을 선택하여 계산됩니다. 작업 \(a\)는 자식 노드로 이동하거나 현재 노드 \(s\)를 확장할 수 있습니다. 이는 가상 노드 기술을 사용하여 트리 검색 에이전트가 지속적으로 비엽 노드를 확장할 수 있도록 합니다.

  \[\text{TreePolicy}(s) = \underset{a \in \text{Children}(s) \cup \{ \emptyset \}}{\arg\max} QUCB(s, a)\]

  행동 \(a\)는 자식 노드로 이동하거나 현재 노드 \(s\)를 확장할 수 있습니다.

• 시뮬레이션(Simulation)

  가치 함수

  \[QUCB(s, a) = Q(s, a) + UCB(s, a) \tag{1}\]

  \(Q(s, a)\)는 선택 기록에서 파생된 작업 값의 샘플 기반 추정치로, 이전 시도에서 고가치 후보를 검색하는 데 사용됩니다. \(UCB(s, a)\)는 상단 신뢰 경계(UCB; Auer, 2002)에 의해 계산된 탐험 보너스로, 상태-작업 쌍 \((s, a)\)의 반복 실행으로 감소합니다.

  값 추정 ($Q(s, a)$는 활용 구성 요소, $UCB(s, a)$는 탐색 보너스)

  \[\quad \forall a \in Children(s) \cup {\varnothing}, Q_{UCB}(s, a) = Q(s, a) + UCB(s, a) \tag{2}\]
• Expansion(확장): 선택 단계에서 지명된 노드를 확장하기 위해 증명 생성 모델을 호출합니다. 이 단계는 표준 MCTS 프레임워크 내에서 단일 롤아웃의 시뮬레이션과 동등합니다. (선택된 노드의 불완전한 증명 코드로 전체 증명 생성 수행, Lean 증명기로 검증)
• Backpropagation(역전파): 각 트리 검색 반복의 마지막 단계는 선택 궤적을 따라 루트에서 확장된 노드까지 값 통계를 업데이트하는 것입니다. (트리 정책 관련 값 갱신. 선택 궤적 $\tau$에 대해 $Q_{UCB}(s, a)$ 갱신)

3.3 몬테카를로 트리 검색을 위한 내재된 보상

공식 정리 증명의 검색 문제에서 외재적 보상은 희소합니다. 이 문제를 해결하기 위해, 내재된 보상을 구성하여 에이전트가 외재적 보상뿐만 아니라 상호 작용 환경에 대한 일반적인 정보를 획득하도록 장려하는 RMaxTS 알고리즘을 제시합니다.

1. RMax를 MCTS에의 적용: 상태 공간의 넓은 범위 탐색을 위한 내재적 보상 구성

2. 내재적 보상 함수 ($\tau$는 가장 최근의 선택 궤적)

   \[\quad R_{intrinsic}(\tau) = \mathbb{I}[\text{at least one new node is added to the search tree}] \tag{3}\]

3. 비정상 보상을 위한 UCB: UCB1 대신 할인된 상한 신뢰 구간(DUCB) 사용

   \[\quad Q_{UCB1}(s, a) = \frac{W(s, a)}{N(s, a)} + \sqrt{\frac{2 \ln \sum_{a'} N(s, a')}{N(s, a)}} \tag{4}\] \[\quad W(s, a) = \sum_{\tau \in \Gamma(s,a)} R(\tau) \tag{5}\] \[\quad N(s, a) = |\Gamma(s, a)| \tag{6}\]

   $\Gamma(s, a)$는 $(s, a)$를 중간 선택 단계로 포함하는 트리 정책 궤적 $\tau$의 목록

4. DUCB 방법

   \[\quad Q_{DUCB}(s, a) = \frac{W_\gamma(s, a)}{N_\gamma(s, a)} + \sqrt{\frac{2 \ln \sum_{a'} N_\gamma(s, a')}{N_\gamma(s, a)}} \tag{7}\] \[\quad W_\gamma(s, a) = \sum_{t=1}^{N(s,a)} \gamma^{N(s,a)-t}R(\tau_t) \tag{8}\] \[\quad N_\gamma(s, a) = \sum_{t=0}^{N(s,a)-1} \gamma^t \tag{9}\]

   $\gamma \in (0, 1)$는 할인 인자로, 오래된 피드백 기록을 부드럽게 제거함.

3.4 몬테카를로 트리 검색의 병렬화

1. 루트 병렬화: 노드당 256개 MCTS 러너, GPU당 하나의 언어 모델 사용
2. 트리 병렬화: 32개 스레드 작업자로 각 탐색 트리 관리, 트리 반복 단계 병렬화
3. 가상 손실: 동시 스레드 작업자 간 다양한 노드 선택 장려를 위해 진행 중인 반복에 대해 가상 보상 $R(\tau) = 0$ 할당

MCTS의 효율성을 향상시키기 위해 여러 병렬화 기법을 도입합니다. 루트 병렬화는 여러 MCTS 러너를 각 노드에 배치하고, 트리 병렬화는 각 검색 트리를 관리하여 증명 생성 및 검증 작업을 균형있게 조정합니다.

3.5 기존 방법과의 비교

증명 트리 검색 방법은 전체 증명 생성과 다단계 증명 단계 생성의 두 가지 전략을 효과적으로 결합합니다. 이 접근 방식은 단일 통과 접근 방식과 유사하게 시작하지만, 정교한 축소 및 재개 메커니즘을 구현하여 확장되며, 이런 반복적 과정은 몬테카를로 트리 검색을 효과적으로 구현하며, 단일 모델을 훈련하여 두 전략을 동시에 지원할 수 있습니다.

4. 실험 결과

4.1 주요 결과

DeepSeek-Prover-V1.5는 두 가지 벤치마크를 사용하여 정리 증명 능력을 평가합니다. 고등학교 수준의 연습 문제와 경쟁 문제를 포함하는 miniF2F, 그리고 대학 수준의 정리에 해당하는 ProofNet입니다. 이 모델은 동일한 훈련된 모델과 인퍼런스 구성을 사용하여 완전한 증명 생성 및 몬테카를로 트리 검색 방법의 결과를 제시합니다.

• 일반적인 목적 모델: GPT-3.5와 GPT-4는 다양한 작업에 효과적인 생성 AI 모델로, 이 중 정리 증명에 특별히 설계되지는 않았지만, 그 규모가 큰 파라미터 덕분에 상당한 능력을 제공합니다.
• 수학 전문화 모델: GPT-f는 정리 증명 작업에 대한 증명 단계 생성을 위해 Transformer를 적용한 초기 노력을 대표하며, 이후 ReProver, LLMStep, Lean-STaR 등의 발전이 있었습니다.

4.2 성능 비교

DeepSeek-Prover-V1.5의 성능을 K번의 시도 내에 정확한 증명을 생성할 수 있는 능력으로 측정하는 pass@K 정확도 메트릭을 사용하여 최신 모델과 비교합니다. 다양한 방식의 샘플링 예산 K를 정의하여 계산 예산을 다른 생성 스키마와 일치시킵니다.

• Single-Pass Sampling Method: $ K $ represents the total number of proofs generated. In this method, a fixed number of proof attempts are made, with $ K $ directly reflecting the quantity of attempts to find a solution without revisiting or refining past attempts.
• Best-First Search Method: $ K $ is given by $ N \times S \times T $, where $ N $ is the number of best-first search attempts, $ S $ is the number of tactics generated for each expansion, and $ T $ is the number of times the expansion is iterated. This method prioritizes expanding the most promising partial solutions first, generating tactics to explore these solutions further and iterating the process to refine the proof search.
• Tree Search Method: $ K $ is calculated as $ N \times T $, where $ N $ is the number of tree search attempts and $ T $ represents the number of model invocations per tree expansion. In this approach, a search tree is constructed with each node representing a state or step in the proof process. The model generates multiple tactics at each node, and the tree expands by exploring the most promising branches based on a heuristic or predefined criteria.

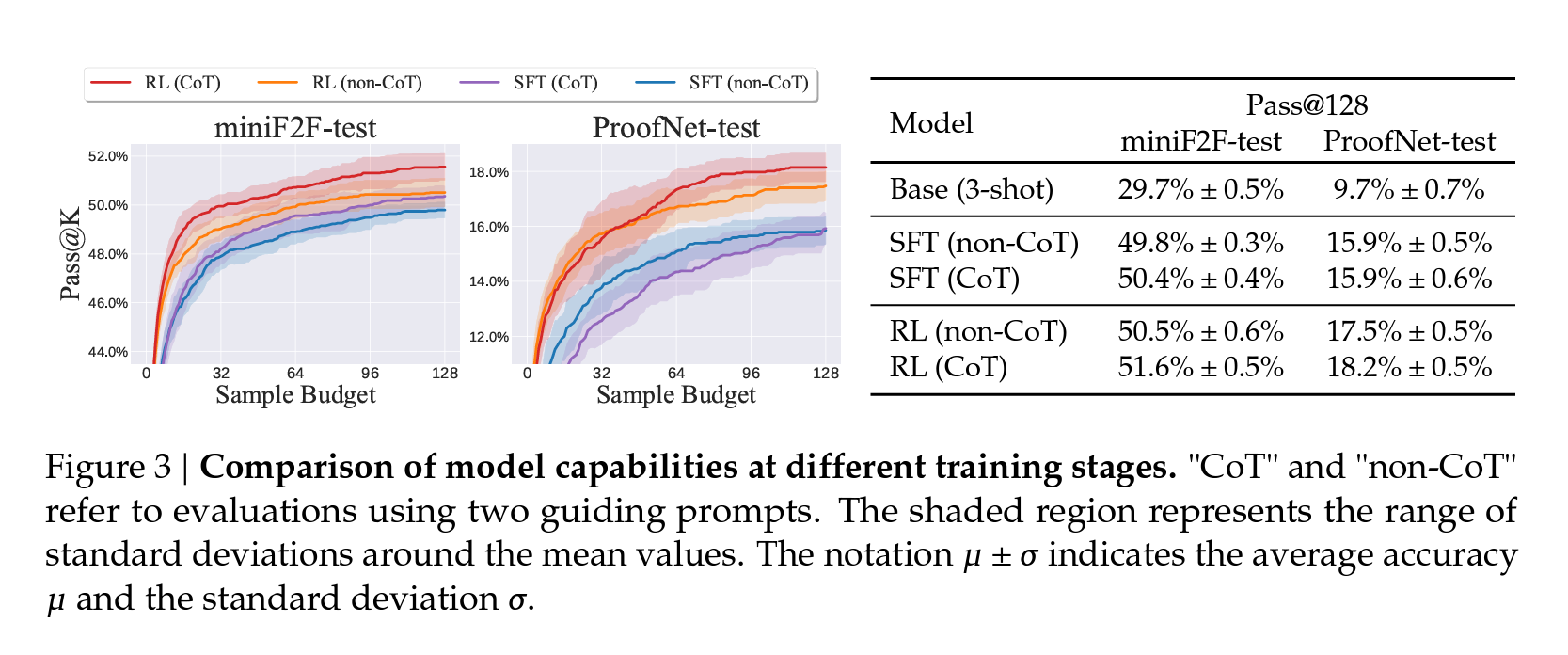
Figure 3. Comparison of model capabilities at different training stages. “CoT” and “non-CoT” refer to evaluations using two guiding prompts. The shaded region represents the range of standard deviations around the mean values. The notation 𝜇 ± 𝜎 indicates the average accuracy 𝜇 andthe standard deviation 𝜎.

“CoT”와 “non-CoT”는 서로 다른 두 가지 안내 프롬프트를 사용한 평가

Benchmarks. We evaluate theorem-proving performance on the following benchmarks to compare model capabilities after each training stage.

miniF2F 검증 결과

DeepSeek-Prover-V1.5-RL은 단일 통과 전체 증명 생성 설정에서 60.2%의 가장 높은 통과율을 달성하여 기존의 DeepSeek-Prover-V1의 50.0%보다 10.2% 포인트 향상되었습니다. 128회의 샘플링 예산으로 51.6%의 문제를 증명함으로써 다른 전체 증명 생성 방법을 크게 능가했으며, 선도적인 트리 검색 방법과 비교할 수 있습니다. 특히 DeepSeek-Prover-V1.5-RL은 전체 증명 생성 샘플링 3200회만에 54.9%의 통과율을 달성하여 기존 최고 성과인 InternLM2-StepProver의 54.5%를 능가했습니다.

ProofNet 검증 결과

DeepSeek-Prover-V1.5-RL은 단일 통과 전체 증명 생성 설정에서 ProofNet 데이터셋 전체에 대해 22.6%의 통과율을 달성하고, RMaxTS 강화를 통해 25.3%로 향상되었습니다. 이 결과는 기존의 최고 성과인 ReProver(13.8%)와 InternLM2-StepProver(18.1%)를 뛰어넘었습니다. 전체 증명 생성 시도가 3200회로 제한될 때, DeepSeek-Prover-V1.5는 정리의 21.7%를 증명하여 기존 최고 성과를 3.6% 향상시켰습니다.

4.3 대규모 샘플링에 대한 훈련 전략의 효과 재검토

DeepSeek-Prover-V1.5-RL은 온라인 강화 학습을 통한 검증 피드백이 모델 능력을 일반적으로 향상시킨다는 주장을 지원하기 위해 SFT 버전과 비교됩니다. 결과는 DeepSeek-Prover-V1.5-RL이 모든 생성 설정에서 SFT 모델을 일관되게 능가하며, RMaxTS와 함께 사용될 때 성능을 추가로 향상시킬 수 있음을 보여줍니다. CoT 프롬프팅과 RMaxTS를 통합함으로써 DeepSeek-Prover-V1.5-RL은 miniF2F-test에서 62.7%의 통과율을 달성하여 SFT 모델보다 3.7% 향상된 성과를 보여줍니다.

이 연구 결과는 DeepSeek-Prover-V1.5가 다양한 증명 생성 방식에서 향상된 성능을 발휘하며, 특히 복잡한 문제에서 더 높은 효율과 효과를 제공함을 보여줍니다.

5. 결론, 한계점 및 향후 연구

DeepSeek-Prover-V1.5는 7억 개의 파라미터를 가진 언어 모델로, Lean 4에서 공식 정리 증명에 있어 모든 오픈 소스 모델을 능가합니다. 이 모델은 수학적 인퍼런스에 특화된 코퍼스를 사용하여 DeepSeekMath-Base 7B의 사전 훈련을 확장한 DeepSeek-Prover-V1.5-Base로 초기화되었습니다. 광범위한 수학 분야에서 다양한 공식 정리를 포함하는 포괄적인 Lean 4 코드 완성 데이터셋에 대한 Supervised learning이 수행되었습니다. 이후, GRPO를 사용하여 온라인 강화 학습을 통해 전체 증명 생성을 강화합니다. DeepSeek-Prover-V1.5 모델 개발을 통해, 문제 해결 능력을 향상시키기 위해 광범위한 탐색과 심층적인 탐험을 통한 몬테카를로 트리 검색의 변형인 RMaxTS를 도입했습니다. 이런 구성 요소들은 LLM 기반 증명 보조 도구를 훈련하기 위한 종합적인 파이프라인을 형성하며, DeepSeek-Prover-V1.5가 DeepSeek-Prover-V1을 개선합니다.

한계점

DeepSeek-Prover-V1.5의 프레임워크는 공식 정리 증명을 위한 AlphaZero 유사 파이프라인을 확립하려고 설계되었습니다. 전문가 반복과 합성 데이터의 사용은 강화 학습의 핵심 시행착오 루프를 반영하며, 컴파일러 오라클은 환경적 감독을 제공하는 세계 모델로 기능합니다. RL 패러다임 내에서, 통합된 트리 검색 모듈은 다양한 도메인에서 초휴먼 성능을 향상시키는 데 효과적임이 입증되었지만, 증명 검색의 주된 문제인 활용 측면은 아직 탐구되지 않았습니다. 미래의 유망한 방향은 불완전한 증명을 평가하고 검색 분기를 정리하는 비평가 모델을 훈련하는 것입니다.

향후 연구

최근의 연구는 개별 정리 증명을 넘어 복잡한 다중 정리 Lean 파일에서 실제 이론 증명을 다루는 방향으로 진전되었습니다. 이는 전체 증명 생성 접근 방식의 자연스러운 확장입니다. 관찰에 따르면 현재 모델은 이미 파일 수준의 컨텍스트에 대한 일부 이해를 갖고 있습니다.

[참고자료 1] Tree Policy 및 UCB Value Estimation

Tree Policy (논문의 식 3)

현재 상태 $s$에서, 가능한 모든 액션(자식 노드로 이동하거나 현재 노드를 확장하는 것) 중에서 $QUCB(s, a)$ 값을 최대화하는 액션을 선택합니다. 이는 탐색(exploration)과 활용(exploitation) 사이의 균형을 맞추는 역할을 합니다. 다음 식은 Monte-Carlo Tree Search (MCTS)에서 사용되는 트리 정책을 나타냅니다.

• $\text{TreePolicy}(s)$: 현재 상태 $s$에서의 트리 정책
• $\arg \max$: 주어진 함수를 최대화하는 인자(argument)를 선택하는 연산자
• $a \in \text{Children}(s) \cup {\emptyset}$: 액션 $a$는 현재 노드 $s$의 자식 노드들($\text{Children}(s)$)과 특별한 토큰 $\emptyset$ (현재 노드를 확장하는 것을 의미)의 집합에서 선택
• $QUCB(s, a)$: Upper Confidence Bound (UCB) 알고리즘을 사용한 상태-행동 가치 함수

UCB Value Estimation (논문의 식 4)

UCB 알고리즘을 사용한 상태-행동 가치 추정을 식으로 나타내면 다음과 같습니다.

• $\forall a \in \text{Children}(s) \cup {\emptyset}$: 모든 가능한 액션 $a$에 대해 (자식 노드들과 현재 노드 확장 포함)
• $QUCB(s, a)$: UCB 알고리즘을 사용한 상태-행동 가치 함수
• $Q(s, a)$: 상태 $s$에서 액션 $a$를 취했을 때의 예상 가치를 나타냅니다. 이는 이전 시도들로부터 얻은 샘플 기반 추정치
• $UCB(s, a)$: Upper Confidence Bound 항으로, 탐색 보너스를 제공

UCB 알고리즘을 사용한 상태-행동 가치는 두 부분으로 구성됩니다.

• 1) 활용(Exploitation) 항: $Q(s, a)$는 이전 시도들로부터 얻은 경험적 가치를 표현
• 2) 탐색(Exploration) 항: $UCB(s, a)$는 덜 방문된 상태-행동 쌍을 탐색하도록 장려하는 보너스를 제공

이 두 항의 합은 각 상태-행동 쌍의 낙관적인 추정치를 제공하며, 이는 높은 확률로 실제 가치의 상한(upper bound)이 됩니다. 이를 통해 MCTS 알고리즘은 유망한 경로를 효과적으로 탐색하면서도 새로운 가능성을 놓치지 않도록 합니다.

본 블로그에서 UCB 및 멀티-암 슬롯 머신을 키워드로 검색하여 참고