Model | Mamba-2, Transformers to SSMs
- Related Project: Private
- Category: Paper Review
- Date: 2024-08-18
Transformers to SSMs: Distilling Quadratic Knowledge to Subquadratic Models
- url: https://arxiv.org/abs/2408.10189
- pdf: https://arxiv.org/pdf/2408.10189
- html: https://arxiv.org/html/2408.10189v1
- huggingface: https://huggingface.co/docs/transformers/main/en/model_doc/mamba2
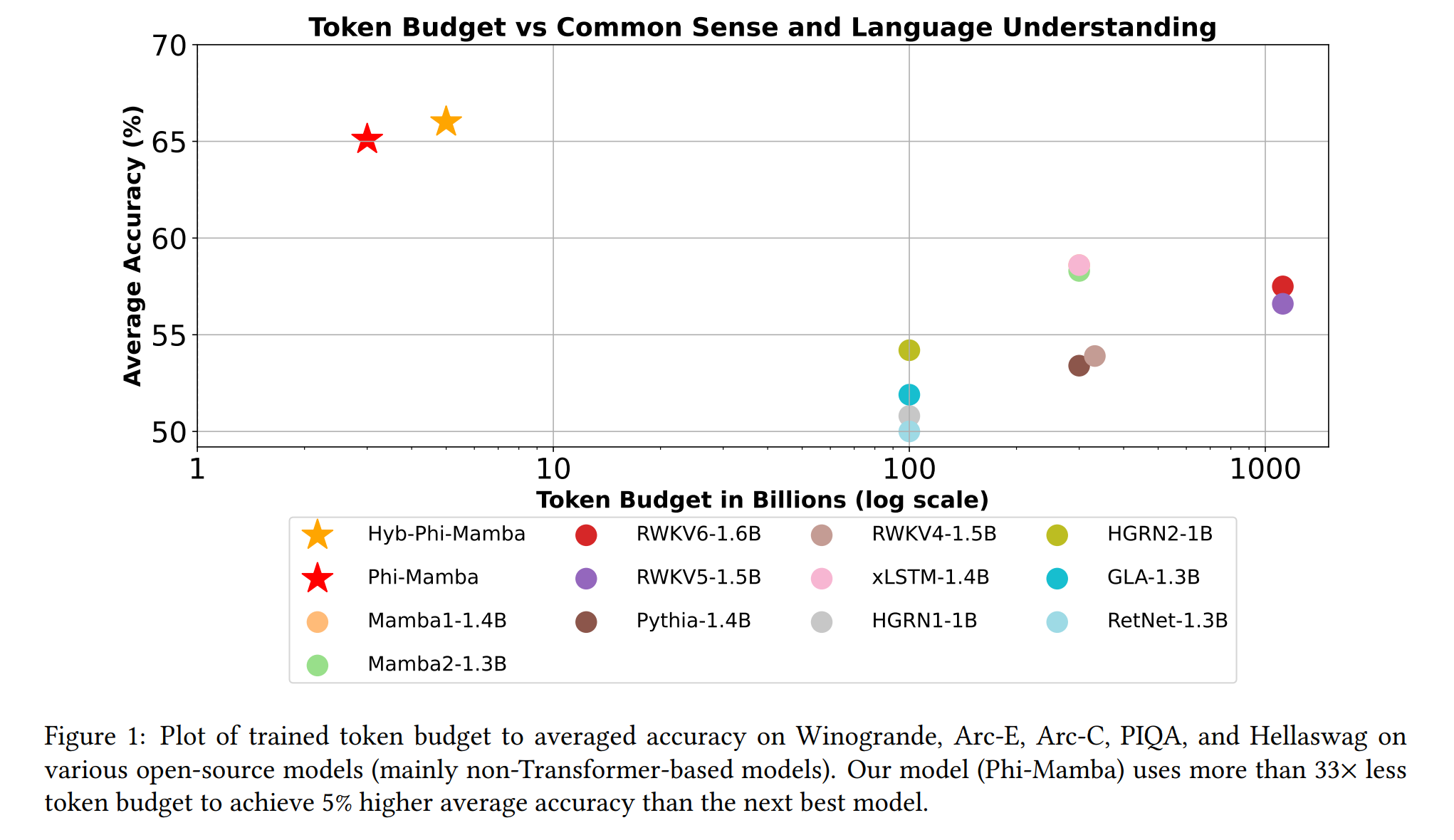
- abstract: Transformer architectures have become a dominant paradigm for domains like language modeling but suffer in many inference settings due to their quadratic-time self-attention. Recently proposed subquadratic architectures, such as Mamba, have shown promise, but have been pretrained with substantially less computational resources than the strongest Transformer models. In this work, we present a method that is able to distill a pretrained Transformer architecture into alternative architectures such as state space models (SSMs). The key idea to our approach is that we can view both Transformers and SSMs as applying different forms of mixing matrices over the token sequences. We can thus progressively distill the Transformer architecture by matching different degrees of granularity in the SSM: first matching the mixing matrices themselves, then the hidden units at each block, and finally the end-to-end predictions. Our method, called MOHAWK, is able to distill a Mamba-2 variant based on the Phi-1.5 architecture (Phi-Mamba) using only 3B tokens and a hybrid version (Hybrid Phi-Mamba) using 5B tokens. Despite using less than 1% of the training data typically used to train models from scratch, Phi-Mamba boasts substantially stronger performance compared to all past open-source non-Transformer models. MOHAWK allows models like SSMs to leverage computational resources invested in training Transformer-based architectures, highlighting a new avenue for building such models.
Release Date: 2023.02
- Content-based reasoning capability
- Efficient on long sequences
- State-of-the-art performance across modalities
Release Date: 2024.08
- Trained with minimal data (3-5B tokens)
- Leverages pre-existing Transformer knowledge
- Superior performance among non-Transformer models
Overview
- Mamba-2는 기존 Transformer 모델의 지식을 활용하여 적은 양의 데이터로 효과적으로 학습(증류)
- Transformer와 SSM의 장점을 결합한 하이브리드 모델 제안 (Hybrid Phi-Mamba, 섹션 3 참조)
- 그러나 아직 일부 실험 셋팅에서의 논증 등
| 특징 | Mamba | Mamba-2 (Phi-Mamba) |
|---|---|---|
| 아키텍처 | Selective State Space Model (SSM) | Selective State Space Model (SSM) |
| 학습 방식 | From scratch | Transformer 모델에서 증류 (distilled) |
| training dataset 양 | 대규모 (정확한 양 명시되지 않음) | 3B 토큰 (Phi-Mamba), 5B 토큰 (Hybrid Phi-Mamba) |
| 기반 모델 | 독립적인 아키텍처 | Phi-1.5 아키텍처 기반에 일부 어텐션 레이어 증류 |
| 주요 장점 | - 선형 시간 복잡도 - 긴 시퀀스 처리 효율적 - 다양한 모달리티에서 우수한 성능 |
- Transformer의 강점 활용 - 적은 training dataset로 효과적인 성능 - 기존 Transformer 리소스 활용 가능 |
| 인퍼런스 속도 | Transformer 대비 5배 빠름 | 구체적인 수치 언급 없음, 하지만 선형 시간 복잡도 유지 |
| 성능 비교 | 같은 크기의 Transformer 모델 능가 실험 | 모든 오픈소스 비-Transformer 모델 중 최고 성능 실험 |
| 주요 개선 | 선택적 상태 공간 (Selective State Space) 도입 | MOHAWK: Transformer에서 SSM으로의 효과적인 지식 증류 방법 제시 |
| 확장성 | 백만 길이 시퀀스까지 성능 향상 | 구체적인 언급 없음, 하지만 SSM의 특성상 긴 시퀀스 처리 가능 |
| 하이브리드 버전 | 언급 없음 | Hybrid Phi-Mamba 버전 존재 |
TL;DR
- Transformer 아키텍처는 언어 모델링 분야에서 지배적이지만 self-attention의 시간 제곱의 복잡도 문제를 가지는데(일반적인 문제, 특히 인퍼런스시)
- 본 연구에서는 Transformer를 상태 공간 모델(SSM)과 같은 대체 아키텍처로 증류하는 방법을 제안합니다.
- 제안된 MOHAWK 방법은 효과적으로 Transformer의 학습 자원을 활용하여 SSM의 성능을 향상시킨다. (Mamba-1에서의 문제 정의에서 약간 멀어지고 특장점이 사라지는 느낌이지만…효과적인 증류 방법으로의 활용?)
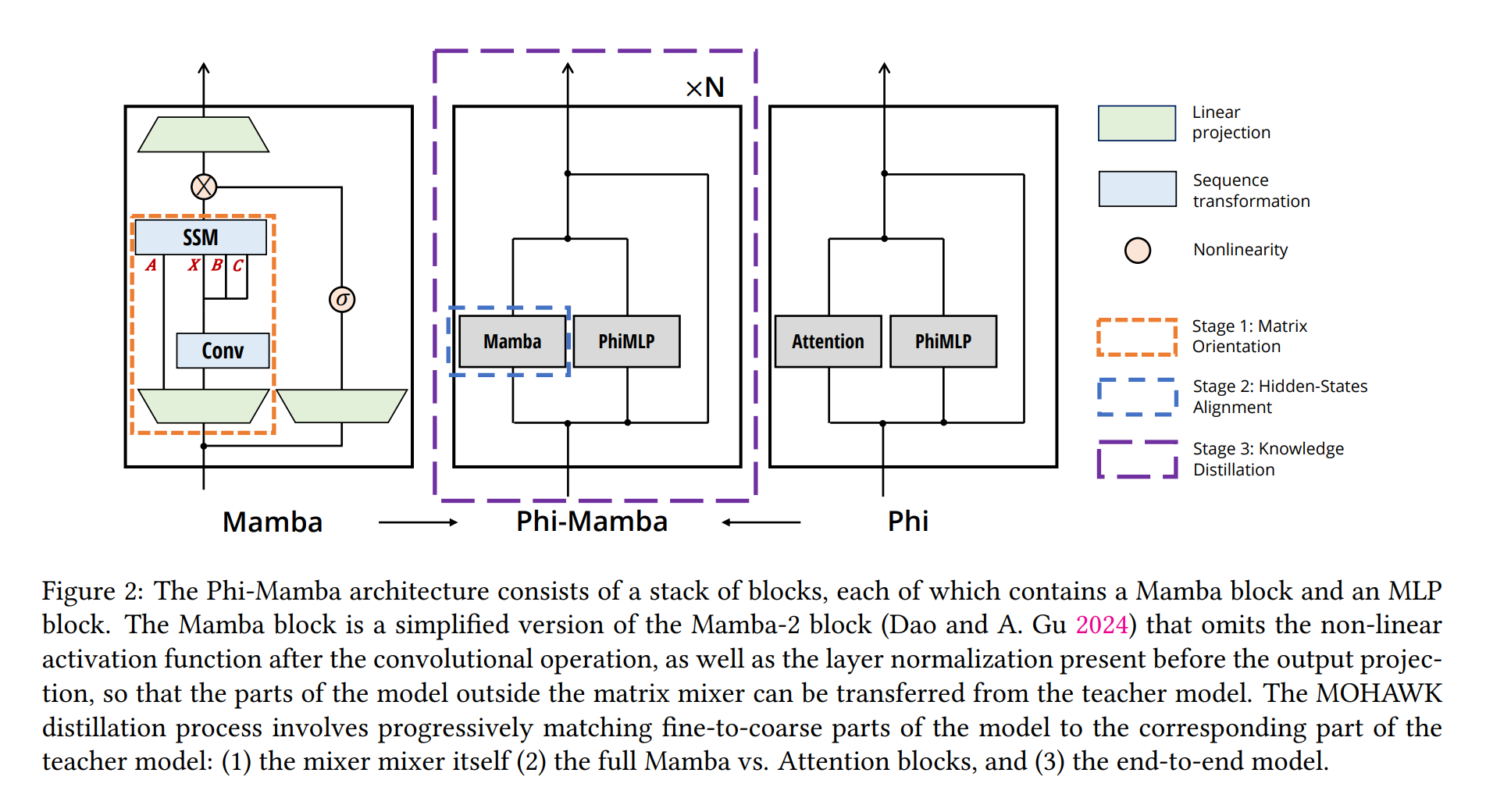
- Student 모델의 행렬 믹서를 Teacher 모델의 셀프 어텐션 행렬과 맞추는 것이 지식 전달의 초기 단계에서 중요했다고 합니다.
- Teacher와 Student 모델 간의 히든 스테이트를 정렬하는 것은 더 정밀한 조정을 가능하게 하여 성능을 개선하는 데 기여했다고 보고합니다.
- 모델 전체의 성능을 Teacher 모델 수준으로 끌어올리기 위해 최종 단계에서는 가중치를 전송하고 전체 모델을 파인튜닝했다고 합니다.
- 어텐션 층과 SSM 레이어를 통합한 하이브리드 모델은 순수 어텐션 트랜스포머 아키텍처의 성능에 근접하면서도 파라미터 수는 적게 사용하여 효율적이었다고 언급합니다.
- Mamba-2와 같은 모델이 트랜스포머와 유사한 상호작용을 학습하고 어텐션을 대체할 수 있음을 보이기 위한 실험과 분석을 수행합니다.
- 시퀀스 믹싱 레이어의 역할과 서브쿼드라틱 모델의 성능에 미치는 영향에 대한 추가 연구가 필요함을 강조하며, 모델의 훈련 가능성과 증류 가능성을 분리해서 고려해야 한다고 언급합니다.
핵심방법
초기화 및 증류 방법을 사용하여 각각의 블록을 조정
- 행렬 정렬 (Matrix Alignment)
- Student 모델의 행렬 믹서를 Teacher 모델의 self-attention 매트릭스와 정렬시키기
- 모든 믹싱 레이어에서 Student 구성 요소를 Teacher 구성 요소와 일치시키기
- Student와 Teacher 모델 간의 self-attention 매트릭스의 거리를 최소화하여 정렬 완성
- Student 모델의 행렬 믹서를 Teacher 모델의 self-attention 매트릭스와 정렬시키기
- 히든 스테이트 정렬 (Hidden State Alignment)
- 최적화 후에도 남아 있는 Student와 Teacher 블록의 출력 차이를 줄이기
- 초기화 및 증류를 통해 두 모델의 출력을 더욱 정렬시키기
- 출력의 L2 노름을 최소화하여 정렬
- 최적화 후에도 남아 있는 Student와 Teacher 블록의 출력 차이를 줄이기
- 가중치 전달 및 지식 전달 (Weight and Knowledge Transfer)
- Student 모델을 Teacher 모델의 성능에 맞게 파인튜닝
- Teacher 모델의 나머지 가중치를 Student 모델로 전달
- Teacher 모델의 로짓 분포를 모방하여 Student 모델을 최적화
- Student 모델을 Teacher 모델의 성능에 맞게 파인튜닝
[참고자료 1] Selective State Space Model
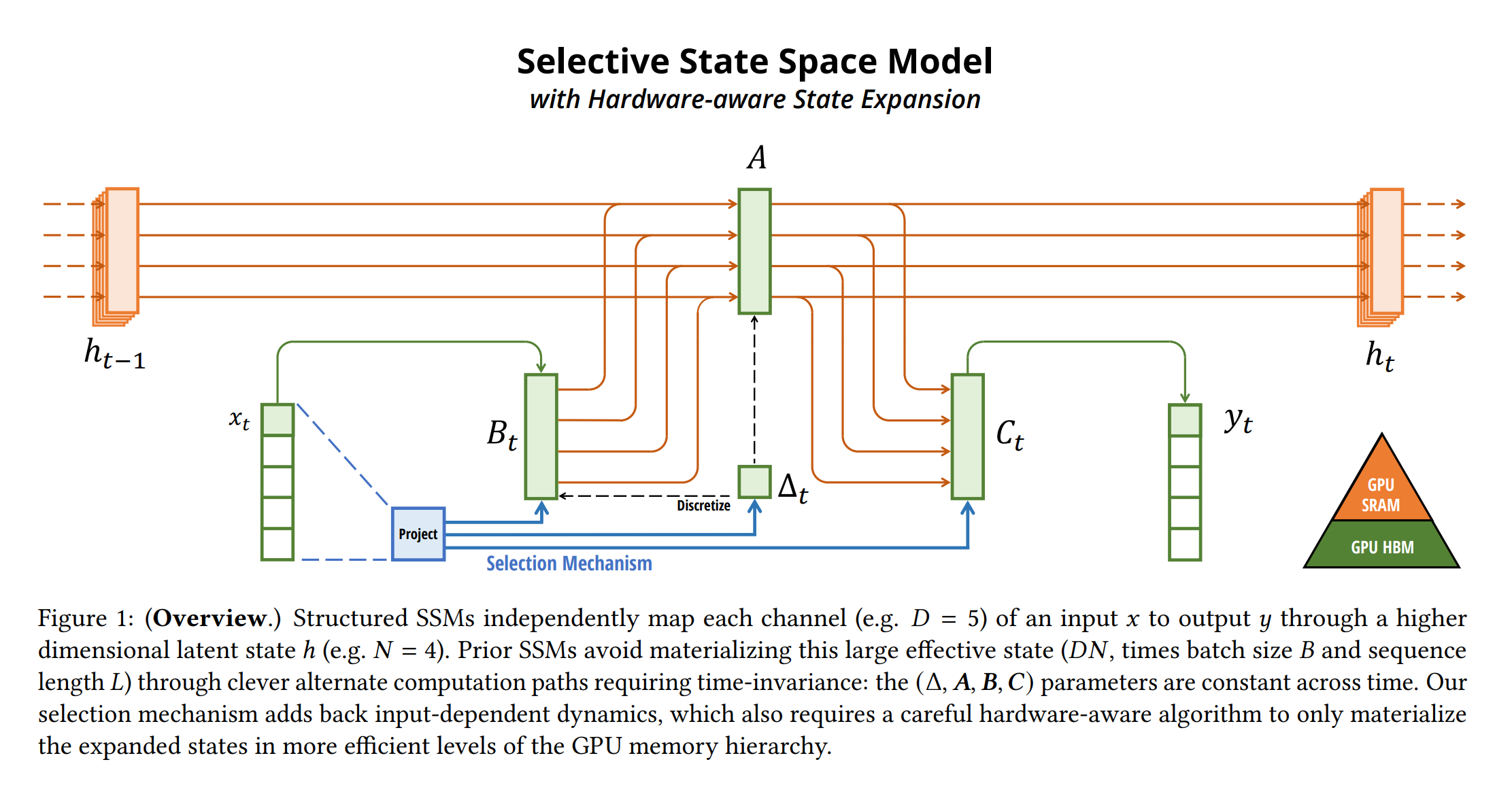
Figure 1: (Overview) Structured SSMs independently map each channel (e.g. 𝐷 = 5) of an input 𝑥 to output 𝑦 through a higher dimensional latent state ℎ (e.g. 𝑁 = 4). Prior SSMs avoid materializing this large effective state (𝐷𝑁, times batch size 𝐵 and sequence length 𝐿) through clever alternate computation paths requiring time-invariance: the (Δ, 𝑨, 𝑩, 𝑪) parameters are constant across time. Our selection mechanism adds back input-dependent dynamics, which also requires a careful hardware-aware algorithm to only materialize the expanded states in more efficient levels of the GPU memory hierarchy.
*출처: Mamba: Linear-Time Sequence Modeling with Selective State Spaces
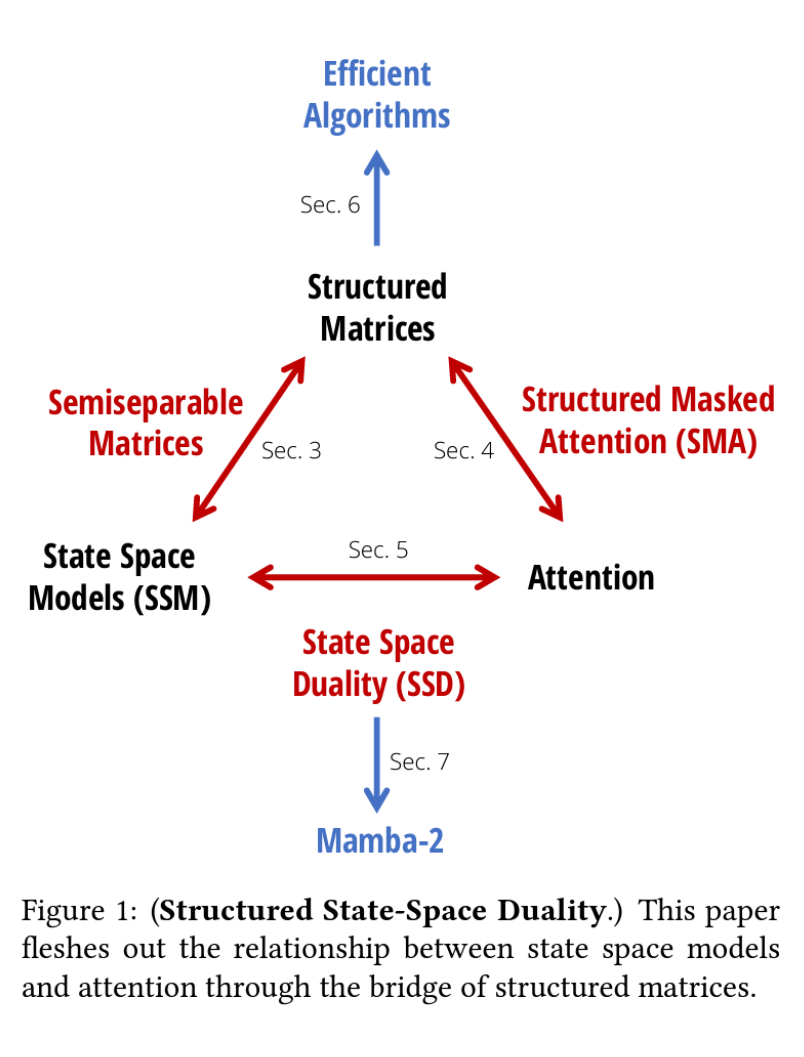
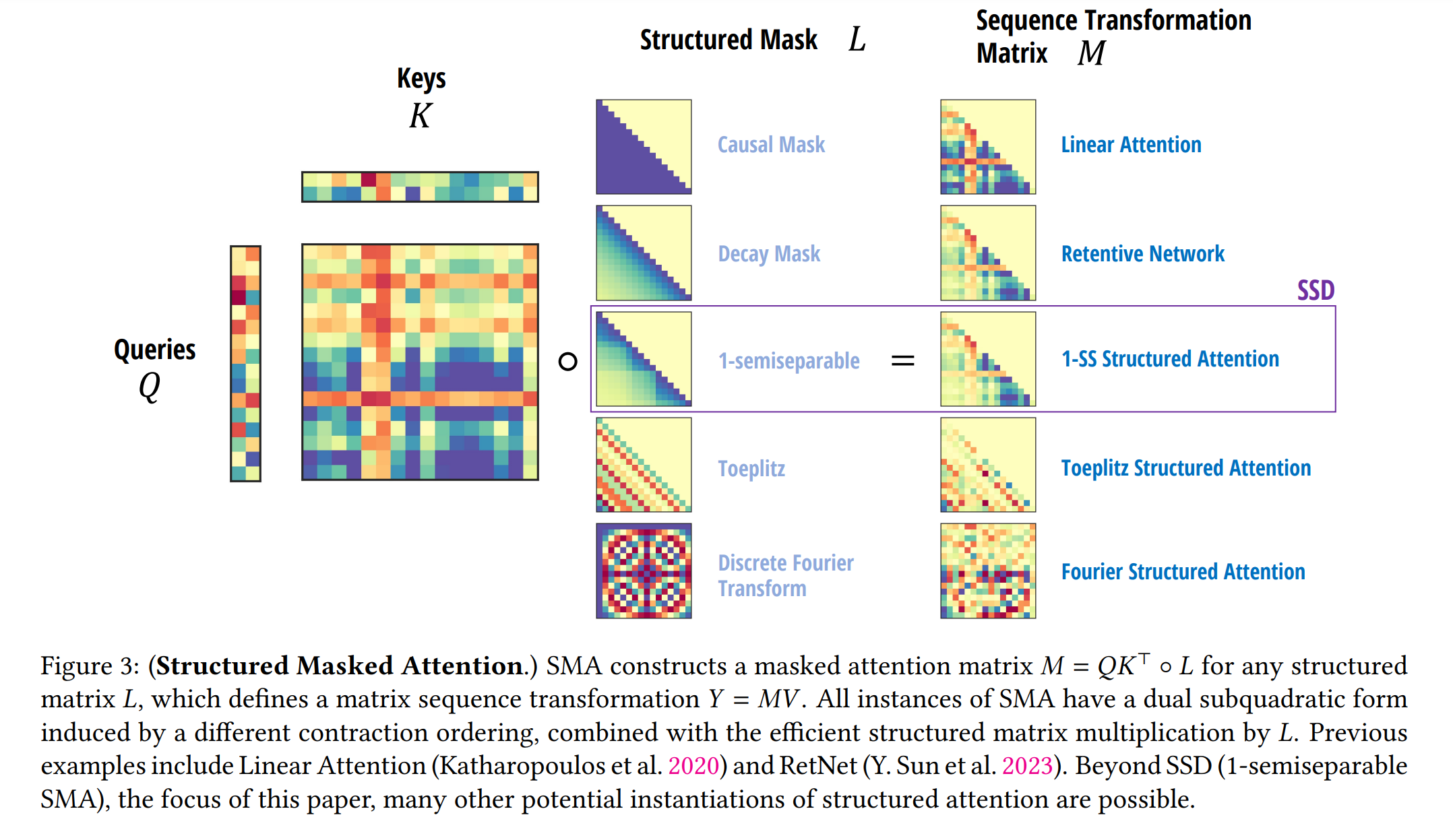
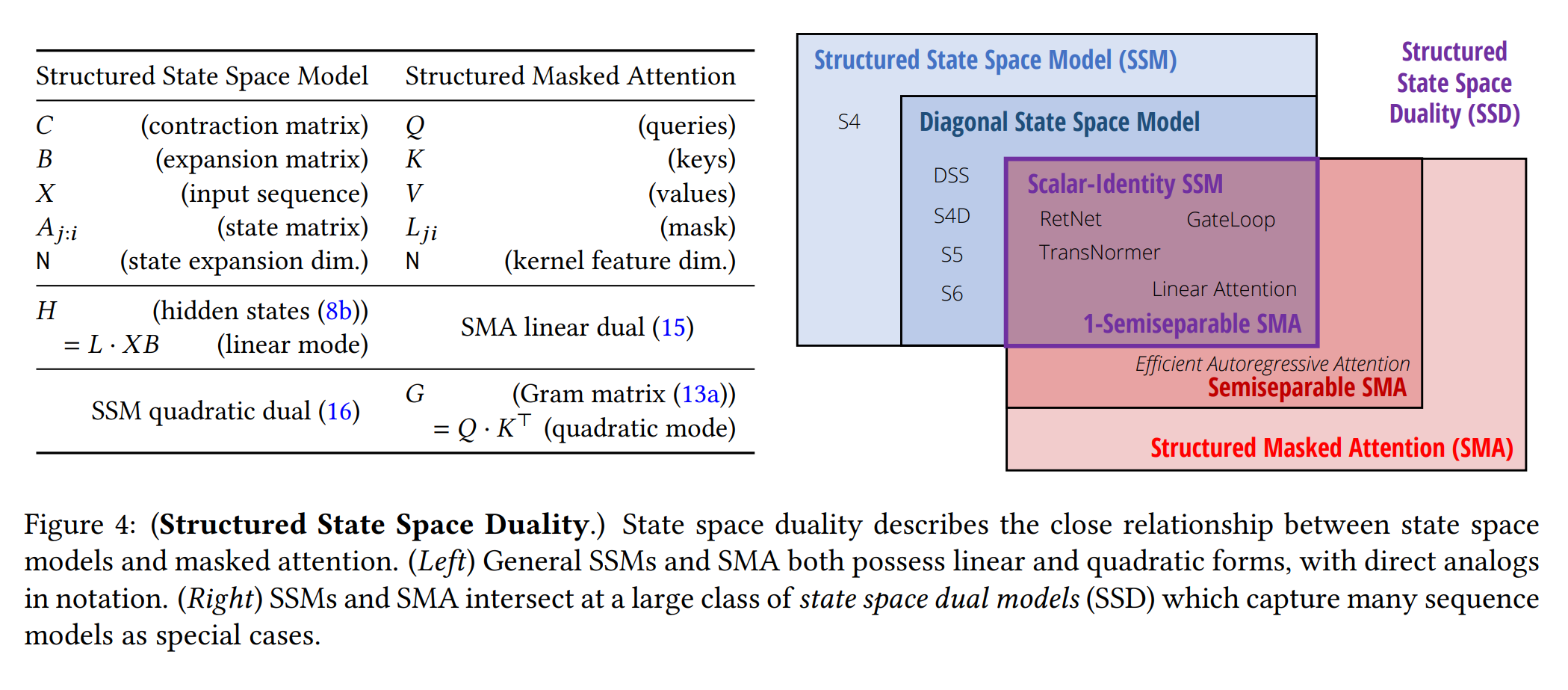
Figure 1: (Structured State-Space Duality.) This paper f leshes out the relationship between state space models and attention through the bridge of structured matrices.
1. 서론
Transformer 기반의 대규모 언어모델은 자연어 처리의 핵심 요소로 자리잡았으나, 모든 위치의 토큰 간 내적을 계산해야 하는 제곱 시간 복잡도의 self-attention에 의존한다는 문제가 있습니다. 이런 문제를 해결하기 위해, 다양한 self-attention 근사 방법 또는 완전히 다른 아키텍처인 상태 공간 모델(SSM) 등의 대안적 모델이 개발되었습니다. 이런 대안 모델은 훈련과 인퍼런스 비용이 저렴하다는 장점은 있지만, Transformer만큼의 커뮤니티 노력이나 계산 자원을 투입받지 못했으므로 이미 훈련된 Transformer 모델을 활용하여 보다 강력한 대안 모델을 개발할 수 있는 방법을 모색하는 것이 중요합니다.
2. 관련 연구
최근 자동 회귀 언어 모델은 대량의 데이터에 대한 사전 훈련을 통해 다양한 downstream 작업에서 향상된 성능을 보여주고 있습니다. Transformer의 제곱 복잡도 문제를 해결하기 위해 RNN, SSM, Linear-attention 메커니즘 등의 서브제곱 대안이 개발되었습니다. 또한, 효율성을 유지하면서 다양한 기능을 결합할 수 있는 하이브리드 모델도 제안되었습니다. GSS는 언어 모델링을 위해 SSM을 게이트 신경망 아키텍처에 통합한 선구자로, 이후 Mamba와 같은 SSM 아키텍처가 도입되었으며, Mamba-2는 Mamba의 간소화 버전으로 더 빠른 속도와 성능을 제공합니다.
본 논문의 접근 방식
본 논문에서는 Transformer와 SSM을 토큰 시퀀스에 대한 다양한 형태의 믹싱 행렬을 적용하는 모델로 간주하고, 이 두 아키텍처 간의 효과적인 증류를 위한 방법을 제안합니다. 접근 방식은 아래의 세 단계로 구성됩니다.
-
행렬 정렬 단계 이 단계에서는 SSM과 Transformer 간의 시퀀스 변환 행렬을 직접 정렬합니다.
\[\text{Matrix Alignment: } A_{\text{SSM}} \approx A_{\text{Transformer}}\] -
히든 스테이트 증류 각 네트워크 블록의 히든 스테이트 표현을 정렬하여 기존에 학습된 표현을 유지하면서 증류합니다.
\[\text{Hidden State Distillation: } H_{\text{SSM}} \approx H_{\text{Transformer}}\] -
최종 단계 훈련 훈련 데이터의 일부만 사용하여 네트워크의 최종 출력을 증류합니다.
\[\text{End-to-End Training: } Y_{\text{SSM}} \approx Y_{\text{Transformer}}\]
본 논문의 접근 방식은 Transformer에서 훈련된 방대한 계산 자원을 활용하여 상태 공간 모델의 성능을 극대화하는 새로운 방법을 제시합니다.
3. 배경 및 개요
본 연구에서는 MOHAWK 방법의 이해를 돕기 위해 필요한 배경 지식과 정의를 제공하고, 이 방법의 기반이 되는 Mamba-2 아키텍처에 대한 개요를 설명합니다.
3.1 행렬 믹서(Matrix Mixers)
시퀀스 모델의 입력과 출력을 대표하는 동등한 기능을 행렬 믹서 또는 시퀀스 변환(sequence transformation)으로 지칭합니다. 공식적으로, 시퀀스 변환은 시퀀스에 대한 파라미터화된 맵으로 정의됩니다.
\(Y = f_{\theta}(X)\) \(X, Y \in \mathbb{R}^{(T, P)}\)
(\(\theta\)는 임의의 파라미터 집합, \(T\)는 시퀀스 또는 시간 축으로 첨자는 첫 번째 차원을 인덱싱)
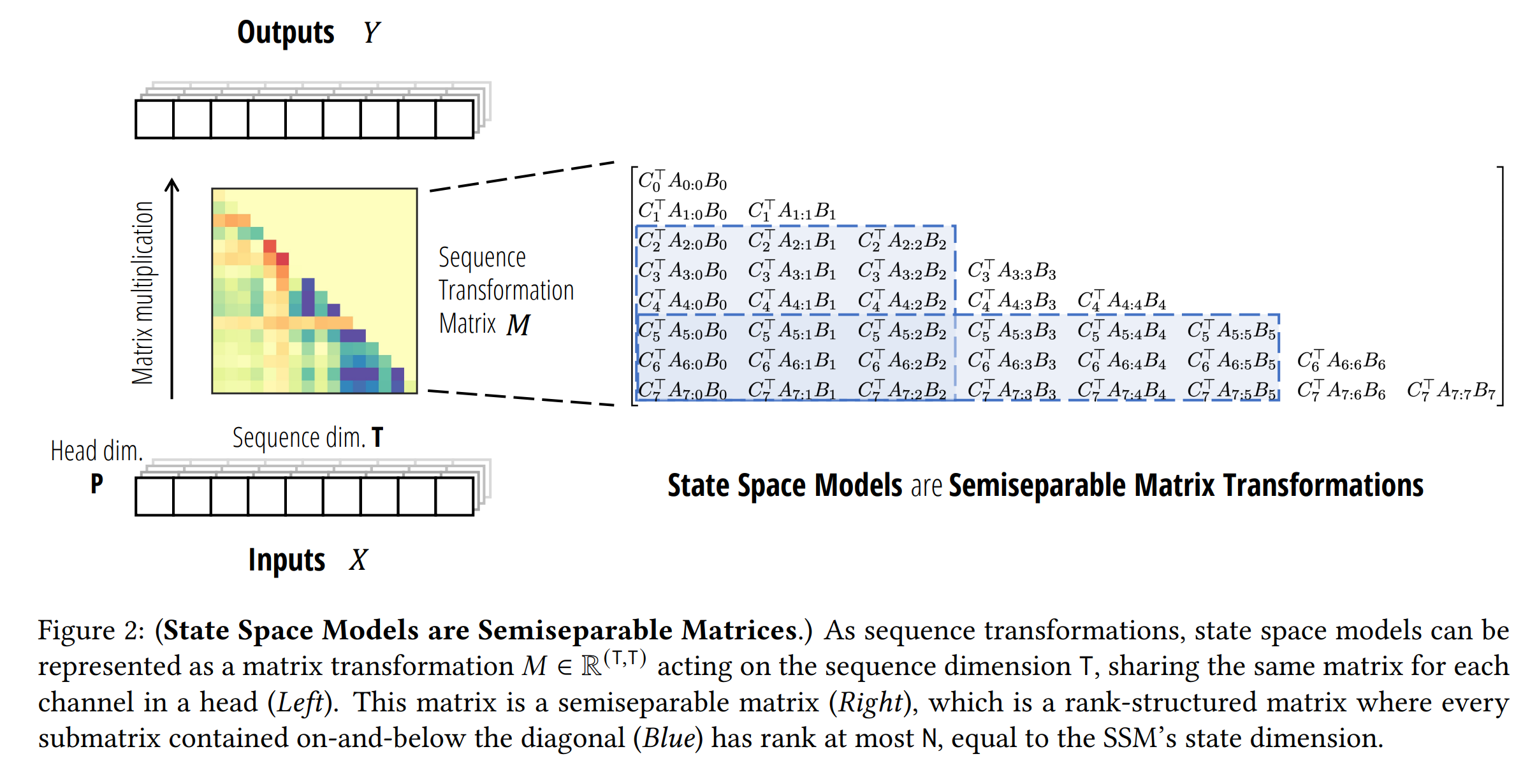
시퀀스 믹서는 다양한 시간 단계의 토큰을 결합하여 모델이 시간 정보와 상호작용을 이해하는 데 도움을 줍니다. 이런 시퀀스 변환은 Transformer와 같은 신경망 프레임워크의 핵심 구성 요소입니다. 특정 시퀀스 변환군은 \(Y = MX\)로 표현될 수 있는데, \(M \in \mathbb{R}^{(T, T)}\)는 시퀀스 변환 행렬 또는 행렬 믹서로 불립니다.
예를 들어, 바닐라 self-attention는 입력 의존적인 \(V\)에 적용되는 \(\text{Softmax}(QK^T)\)으로, 이는 익숙한 \(\text{Softmax}(QK^T)V\) 결과를 생성합니다. 유사하게, Linear-attention(linear attention)는 형태 \(K^T\)의 시퀀스 변환 행렬을 가집니다. \(\text{Softmax}(QK^T)\)와 \(QK^T\)에 하부 삼각 행렬 \(L\)을 곱하여 인과적 변형을 쉽게 얻을 수 있습니다.
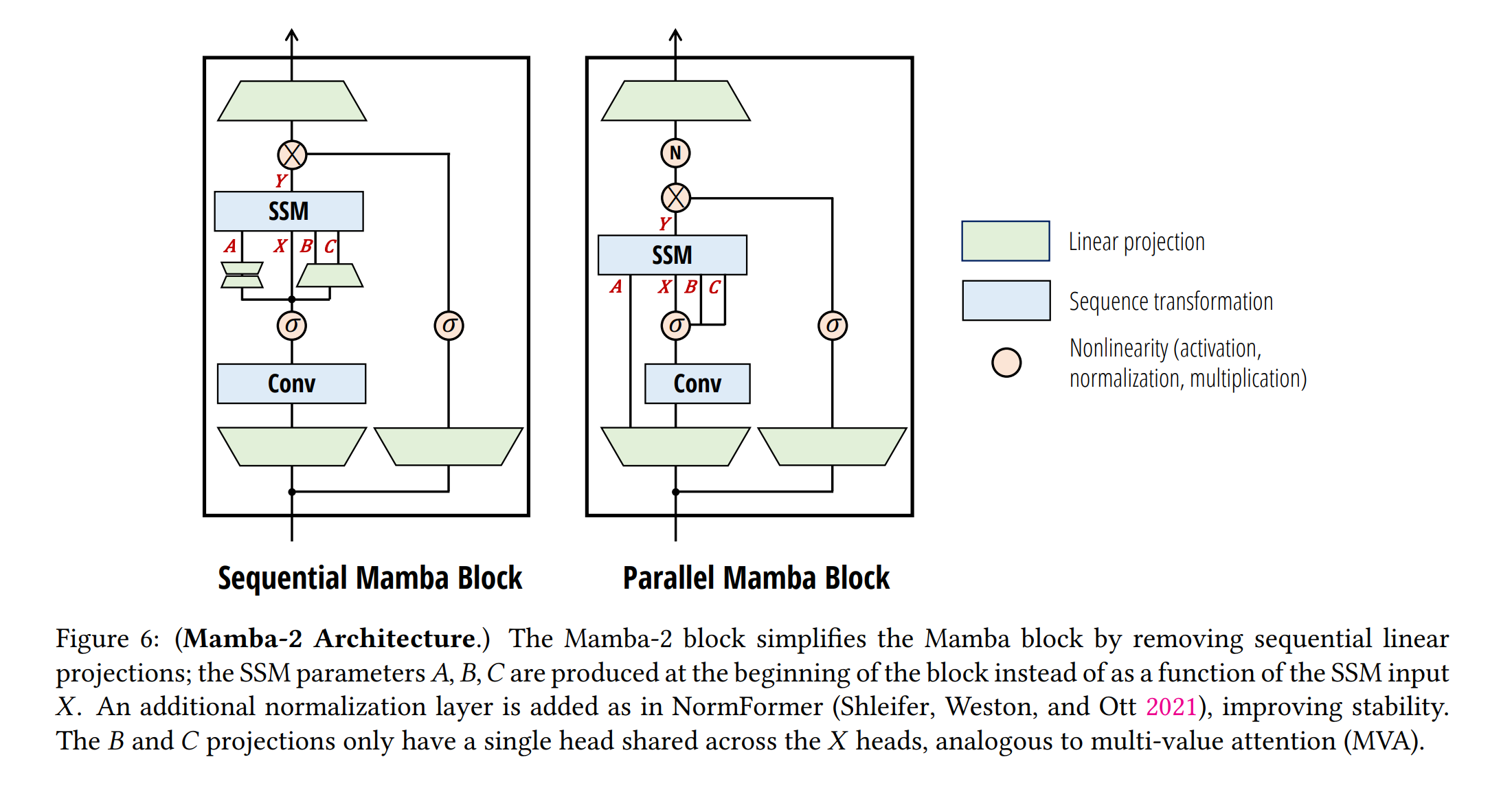
3.2 Mamba-2
Mamba-2는 구조화된 상태 공간 모델(SSM)의 일종으로, 시간 변화하는 상태 공간 모델을 사용하여 입력에 따라 선택적으로 초점을 맞추거나 입력을 무시할 수 있습니다. Mamba-2는 다음과 같이 정의됩니다.
\(h_{t+1} = A_t h_t + B_t x_t\) \(y_t = C_t h_t\)
\(B_t\)와 \(C_t\)는 시스템의 입력 의존적 투영을 나타내며, \(A_t\)는 스칼라 \(\alpha_t\)에 의해 곱해진 항등 행렬 \(I\)입니다. 이는 이전 모델에서 연속 신호가 아닌 이산 신호로부터 시퀀스가 기원한다고 간주하고, 원래 Mamba 모델의 샘플링 구성 요소 \(\Delta t\)를 생략하는 새로운 형식입니다.
Mamba-2는 특히 \(A_t = I\) (Mamba-2에서 \(\alpha_t = 1\)로 더 제한된 경우)를 고정하면 인과적 Linear-attention의 형식을 취할 수 있으며, \(B\)와 \(C\)는 각각 키와 쿼리의 투영을 나타내고, 입력 투영 \(X\)는 값의 투영에 해당됩니다.
\[h_{t+1} = \alpha_t \cdot I h_t + B \cdot x_t\] \[y_t = C \cdot h_t\] \[\Rightarrow \begin{bmatrix} \alpha_1 & 0 & 0 & \cdots & 0 \\ \alpha_2:1 & \alpha_2 & 0 & \cdots & 0 \\ \alpha_3:1 & \alpha_3:2 & \alpha_3 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \alpha_n:1 & \alpha_n:2 & \alpha_n:3 & \cdots & \alpha_n \end{bmatrix} \circ (C \cdot B^T) \cdot X\]Mamba-2 아키텍처는 학습 가능한 인과적 마스크를 가진 인과적 Linear-attention로 볼 수 있습니다. Mamba-2 블록을 더 효과적으로 만들기 위해, 파라미터 투영을 병렬로 추가하고, 최종 출력 투영 전에 정규화 계층을 추가해 더 큰 모델의 훈련에서 불안정성을 해결했다고 합니다.

4. 방법
이 섹션에서는 MOHAWK의 각 단계에 대해 설명합니다. 특히, (4.21) 행렬 정렬, (4.2) 히든 스테이트 정렬, (4.3) 지식 전달의 세 단계를 다루며, 이 세 단계는 모두 사전 훈련된 Transformer 모델에서 효과적인 Student 모델을 개발하는 데 중요합니다. 전통적인 증류 기법과 달리, Student 모델은 Teacher 모델의 전체 아키텍처를 유지하면서, 어텐션 매트릭스 믹서를 서브제곱 대안으로 교체합니다. 이 섹션은 Phi-Mamba 아키텍처와 그 하이브리드 버전에 대한 심층적인 설명으로 마무리됩니다. 해당 방법의 효과 및 어브레이션 연구는 섹션 5에서 논의됩니다.

각 프로세스 별로 Figure를 참고 -(4.1) Step 1: 행렬 정렬 -(4.2) Step 2: 히든 스테이트 정렬 -(4.3) Step 3: 가중치 전달 및 지식 전달
4.1 Step 1: 행렬 정렬
MOHAWK의 첫 번째 단계는 Student 매트릭스 믹서를 Teacher의 self-attention 매트릭스와 정렬하는 것을 목표로 합니다. 이 정렬을 달성하는 것은 두 단계 과정입니다. 먼저, 모든 믹싱 레이어에서 Student 구성 요소를 Teacher의 구성 요소와 일치하도록 설정합니다. 이는 각 레이어의 입력이 매트릭스 믹서 섹션까지 동일한 변환을 거치도록 보장합니다. 따라서 입력에서 믹싱 과정까지의 유일한 변화는 매트릭스 계산입니다. 그런 다음 Student와 Teacher 모델의 각 레이어에서 self-attention 매트릭스와 구체화된 SSM 매트릭스(2) 사이의 거리를 최소화합니다.
\[\min_{\phi} \| \text{TeacherMixer}(u) - \text{StudentMixer}_{\phi}(u) \|_F\]\(\phi\)는 Student의 시퀀스 믹싱 레이어 내 파라미터를 나타내고, \(u\)는 임의의 입력을 나타냅니다. 실험 설정에서 \(u\)는 Teacher 모델의 이전 레이어의 출력으로 선택되어 레이어에 대한 입력 분포를 더 잘 모방합니다. 이 단계는 Student와 Teacher 모델이 대략적으로 유사한 믹싱 레이어를 가지도록 보장하고, 이후 단계의 기초를 마련합니다.
4.2 Step 2: 히든 스테이트 정렬
식 (3)의 최적화 이후에도 Student와 Teacher 블록의 출력 사이의 차이를 다루어야 합니다. 이를 위해 (1) 초기화와 (2) 증류를 사용하여 두 블록의 구성 요소를 추가로 정렬합니다. 구체적으로, 각 Student와 Teacher 믹싱 블록을 일치시키기 위해 출력의 L2 노름을 최소화하는 것을 목표로 합니다. (\(\phi\)는 Student 블록의 파라미터를 나타내고, \(u\)는 입력)
\[\min_{\phi} \| \text{AttnBlock}(u) - \text{StudentMixerBlock}_{\phi}(u) \|_2\]이 단계 역시 Student와 Teacher 블록의 입력이 동일하므로 모든 Student 레이어에서 병렬로 수행될 수 있습니다.
4.3 Step 3: 가중치 전달 및 지식 전달
증류 과정의 마지막 단계는 Student 모델을 Teacher 모델의 성능에 맞추도록 파인튜닝하는 것을 목표로 합니다. 각 Student 믹싱 블록이 해당 Teacher 믹싱 블록과 일치하더라도, 네트워크 전체의 연속 블록 사이에 여전히 불일치가 존재합니다. 이런 격차를 해소하고 언어 모델의 나머지 구성 요소를 다루기 위해, Teacher 모델의 나머지 가중치를 Student의 해당 구성 요소로 전달합니다. Phi-Mamba의 경우, 이는 토큰 임베딩, 최종 레이어 정규화, 언어 모델 헤드, 그리고 각 블록에서의 MLP 및 입력 정규화를 포함합니다. 그런 다음 Teacher 모델의 로짓 분포를 모방하도록 Student 모델을 파인튜닝합니다. 이를 지식 전달이라고 하며, 다음과 같은 손실 함수를 사용합니다. (\(x\)는 입력 토큰)
\[\min_{\phi} \mathcal{L}_{CE}(\text{TeacherModel}(x), \text{StudentModel}_{\phi}(x))\]4.4 Phi-Mamba 아키텍처
MOHAWK의 세 단계를 결합한 Phi-Mamba 아키텍처를 소개합니다. 이 아키텍처는 Mamba-2 모델과 Phi-1.5 Transformer 모델을 통합합니다. 이 아키텍처는 초기화 및 증류로 설명된 이전 섹션들에 따라 Phi-Mamba 블록의 스택으로 구성됩니다. 또한, 하이브리드 Phi-Mamba 변형은 Phi-1.5의 4개의 어텐션 레이어를 유지하여 두 시퀀스 믹서의 강점을 효과적으로 활용합니다.
5. 경험적 검증(Emperical Validation)
본 섹션에서는 MOHAWK를 통해 증류된 Phi-Mamba-1.5B 및 하이브리드 Phi-Mamba-1.5B의 downstream 평가 점수를 검토하며, 이들이 이전의 서브제곱 및 하이브리드 모델을 각각 능가하는 성능을 보임을 실증적으로 보여줍니다. 이들 모델은 또한 시간 및 메모리 복잡성 측면에서 더 나은 결과를 제공합니다.
Mamaba-2, 경험적 검증(Emperical Validation) 및 논증 핵심 색인마킹
5.1 최종 결과
Phi-Mamba-1.5B 및 하이브리드 Phi-Mamba-1.5B는 각각 3억 토큰과 5억 토큰을 사용하여 C4 데이터셋에서 증류되었습니다. 이는 다른 최고 성능의 서브제곱 모델이 사용하는 자원의 1% 미만입니다. 하이브리드 모델은 동일한 데이터셋에서 5억 토큰을 사용했습니다. 이들 모델의 성능은 WinoGrande, HellaSwag, PIQA, ARC-challenge, ARC-easy 및 LAMBADA를 포함한 일반적인 상식 인퍼런스 및 언어 이해 작업에서의 평가 결과로 확인할 수 있습니다.
5.2~5.4 각 단계의 영향 분석
MOHAWK의 세 단계를 각각 분석하여, 학습된 표현을 Student 모델로 전달하는 과정에서 나타나는 효과를 분석합니다. 또한, 이상적인 조건에서 Phi-Mamba 증류 과정을 모델링하기 위해 모든 가중치를 전달하되 어텐션 레이어만 처음부터 초기화한 Phi-1.5를 다른 Phi-1.5로 증류하는 실험도 수행했습니다.
5.5 최종 Phi-Mamba 모델 훈련
세 단계를 통합하여 최종 Phi-Mamba 모델을 증류합니다. 1단계에서 8천만 토큰, 2단계에서 1억 6천만 토큰을 사용하고, 3단계에서 총 30억 토큰을 사용했습니다. 각 단계의 토큰 수는 해당 단계의 성능에 따라 조정되었습니다.
5.6 하이브리드 Phi-Mamba 모델
하이브리드 Phi-Mamba는 4개의 어텐션 레이어만 유지하고 나머지 블록을 Mamba-2 블록으로 변환합니다. 이 모델은 표준 언어 모델링 데이터로 사전 훈련된 비슷한 크기의 하이브리드 모델과 비교하여 향상된 성능을 보여줍니다.
5.7 self-attention 근사 및 대체
Mamba-2의 self-attention과 유사한 상호작용 학습 능력에 대해 더 깊이 파고들어, Mamba-2 시퀀스 트랜스포머가 self-attention 매트릭스를 어느 정도 근사할 수 있는지, 그리고 이 능력이 Phi-1.5와 같은 종단간 언어 모델에서도 나타나는지를 조사합니다.
5.7.1 self-attention 매트릭스 근사
다양한 매트릭스 믹서군이 사전 훈련된 Transformer의 self-attention 매트릭스를 얼마나 잘 매치하는지를 테스트합니다. 이는 Llama2-7b-Chat 모델의 각 레이어에서 샘플을 가져와 주어진 구조화된 매트릭스군에 투영하는 실험을 통해 수행됩니다.
5.7.2 언어 모델에서의 self-attention 대체
Mamba-2 블록이 언어 모델 내의 어텐션 레이어를 대체할 수 있는 능력을 검증하기 위해, Phi-Toeplitz 및 Phi-LR 아키텍처 두 가지를 생성하고 MOHAWK 과정을 통해 10억 토큰으로 각 단계를 실행합니다.
이런 실험들은 Mamba-2가 self-attention의 기능을 효과적으로 대체할 수 있음을 보여주며, 이는 최종 모델의 성능과 밀접하게 연관되어 있습니다. 더욱이, 이런 결과는 Mamba-2의 높은 표현력이 언어 모델에서 중요한 역할을 할 수 있음을 시사합니다.
6. 토론 및 결론
본 연구에서는 Mamba-2 모델이 사전 훈련된 Transformer Teacher 모델로부터 성공적으로 증류될 수 있음을 보여주었습니다. Mamba 모델을 포함한 여러 오픈 소스 모델과 비교할 때 100배 이상 적은 데이터를 사용함에도 불구하고, 서브제곱 모델은 다양한 벤치마크 테스트에서 다른 서브제곱 모델들을 큰 차이로 능가합니다.
MOHAWK 프레임워크의 중요성
MOHAWK 프레임워크의 다단계 과정은 Teacher 모델의 지식을 최대한 추출하는 데 필수적이었습니다. 이는 연구와 훈련 법칙에서 보여진 바와 같이, 점진적으로 증류 범위를 넓혀가는 과정에서 명확하게 드러났습니다. 또한, 하이브리드 Attention-SSM 모델을 증류할 때 MOHAWK의 효과성을 계속해서 발견하고 있으며, 어텐션 레이어의 수와 위치에 대한 어브레이션을 제공합니다.
Mamba-2와 Transformer의 실제적 연관성
이론적으로뿐만 아니라 실제적으로도 Mamba-2가 Transformer와 유사한 상호 작용을 포착할 수 있음이 입증되었습니다. Mamba-2는 성능의 큰 손실 없이 Attention을 대체할 수 있으며, 이는 과거 연구에서 언어 모델의 지식이 MLP 블록에 내재되어 있습니다고 제안한 것과 일치합니다. 충분히 표현력 있는 매트릭스 믹서를 갖춘 어떤 서브제곱 모델이라도 사전 훈련된 Transformer의 행동을 복제할 수 있으며, 이는 서브제곱 모델에 대한 쿼드러틱 지식을 가져올 수 있습니다.
추후 연구 방향
서브제곱 모델에서 시퀀스 믹싱 레이어의 역할과 성능에 미치는 영향을 탐구하는 추가 연구를 권장합니다. 증류 과정과 시퀀스 믹서 아키텍처의 발전은 다양한 작업에서 성능을 더욱 향상시킬 수 있다고 보고하며, "훈련 가능성(trainability)"과 "증류 가능성(distillability)"은 모델의 별개의 속성이므로, 증류 기술은 모델에 더 적절하게 맞춰져야 합니다.
[참고자료 2] Torch Mamba Block
def segsum(x):
"""Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
which is equivalent to a scalar SSM."""
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
return x_segsum
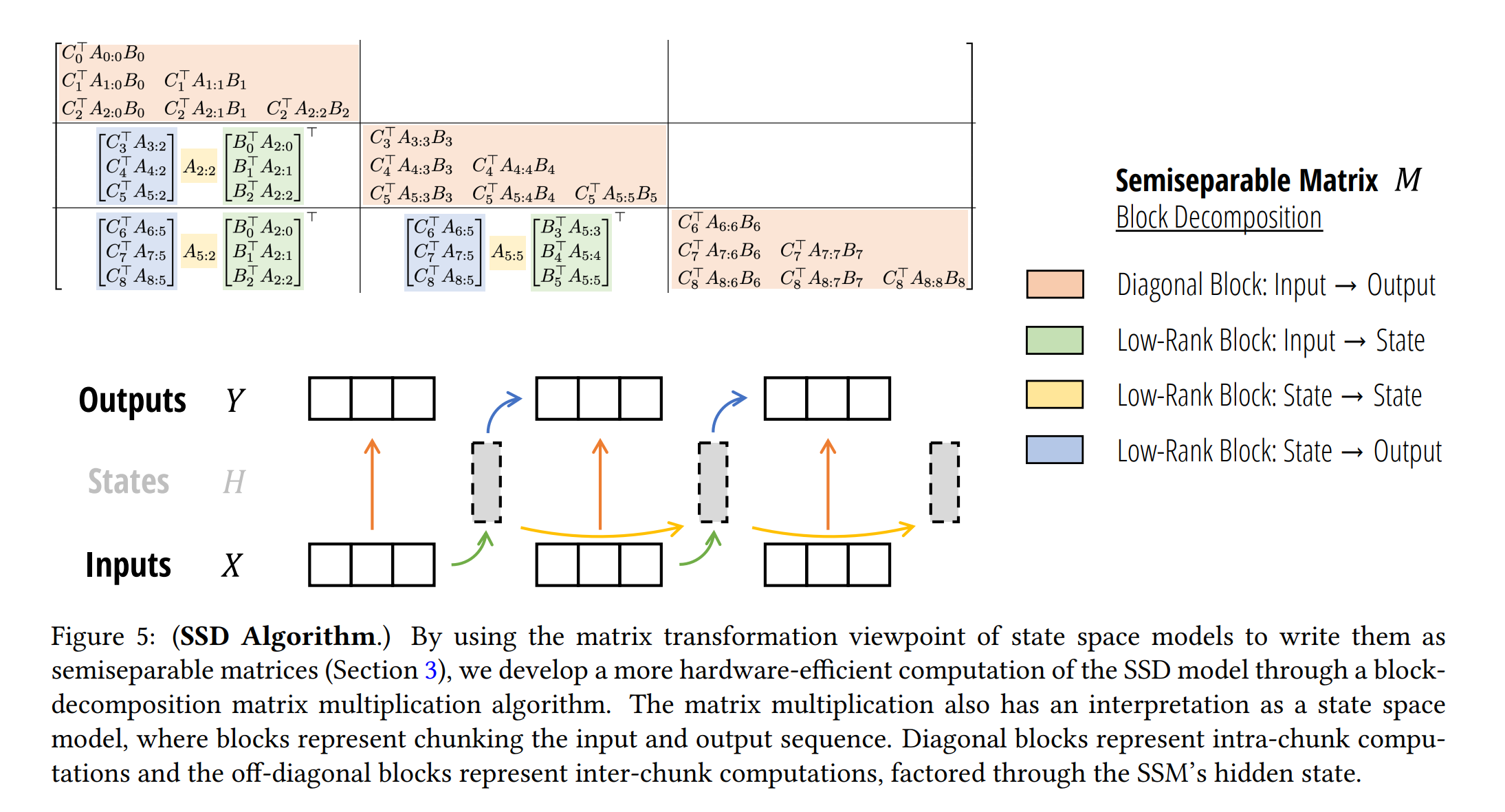
def ssd(X, A, B, C, block_len=64, initial_states=None):
"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""
assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0
# Rearrange into blocks/chunks
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
A_cumsum = torch.cumsum(A, dim=-1)
# 1. Compute the output for each intra-chunk (diagonal blocks)
L = torch.exp(segsum(A))
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)
# 2. Compute the state for each intra-chunk
# (right term of low-rank factorization of off-diagonal blocks; B terms)
decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)
# 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
# (middle term of factorization of off-diag blocks; A terms)
if initial_states is None:
initial_states = torch.zeros_like(states[:, :1])
states = torch.cat([initial_states, states], dim=1)
decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
states, final_state = new_states[:, :-1], new_states[:, -1]
# 4. Compute state -> output conversion per chunk
# (left term of low-rank factorization of off-diagonal blocks; C terms)
state_decay_out = torch.exp(A_cumsum)
Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)
# Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
return Y, final_state