Context Is Not an Array

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-10

Your Context Is Not an Array: Unveiling Random Access Limitations in Transformers

• url: https://arxiv.org/abs/2408.05506
• pdf: https://arxiv.org/pdf/2408.05506
• html: https://arxiv.org/html/2408.05506v1
• abstract: Despite their recent successes, Transformer-based large language models show surprising failure modes. A well-known example of such failure modes is their inability to length-generalize: solving problem instances at inference time that are longer than those seen during training. In this work, we further explore the root cause of this failure by performing a detailed analysis of model behaviors on the simple parity task. Our analysis suggests that length generalization failures are intricately related to a model’s inability to perform random memory accesses within its context window. We present supporting evidence for this hypothesis by demonstrating the effectiveness of methodologies that circumvent the need for indexing or that enable random token access indirectly, through content-based addressing. We further show where and how the failure to perform random memory access manifests through attention map visualizations.

Transformer의 Positional Embedding 관련 이슈로 분석

TL;DR

1. 트랜스포머 기반 대규모 언어모델의 진화는 휴먼 언어와 상호 작용하는 방식에서 새로운 시대를 맞이했습니다.
2. 이런 모델들은 수학적 알고리즘 작업에서 특히 길이 일반화 문제에 어려움을 겪는 것으로 잘 알려져있는데,
3. 콘텐츠 기반 어드레스 지정과 인덱스 기반 어드레스 지정의 차이를 탐구하고, 이런 어려움을 극복하기 위한 접근 방식을 제시합니다.

트랜스포머 모델이 산술 작업을 처리하는 방법을 개선하기 숫자와 위치 정보를 처리하는데 적합한 방법을 도입

본질적으로 숫자의 적절한 의미론적인 토큰을 부여하는 것이 사실상 어렵고(각 수를 의미론적 토큰으로 넣는 것에는 한계가 있으므로), 연산 기호 역시 시퀀스에서 의미론적인 내용을 포함하지 못 하는 것을 앵커와 DP와 비슷한 방법을 사용

기호(Mnemonics) 도입

• 트랜스포머가 산술 연산을 수행할 때 각 숫자의 위치를 정확히 인식하고 기억할 수 있도록 하기 위해
• 각 숫자 앞에 고유한 기호를 배치하여, 모델이 이를 ‘앵커’로 사용 → 모델이 숫자를 처리할 때 위치 정보를 보다 명확하게 인식

스크래치패드 활용

• 숫자를 처리하는 동안 중간 계산값을 저장하고, 이를 반복적으로 참조할 수 있도록 하여 모델이 긴 시퀀스의 숫자를 효과적으로 처리할 수 있게 하기 위해,
• ‘스크래치패드’라는 메모리 공간을 사용하여 각 계산 단계에서의 중간 결과를 저장 → 복잡한 연산을 수행할 때 모델이 이전에 계산된 값을 재활용

어텐션 패턴 최적화

• 모델이 중요한 정보에 집중할 수 있도록 하여 정확도를 높이기 위해,
• 모델의 어텐션 매커니즘을 조정하여 중요한 토큰(숫자와 기호)에 더 많은 ‘주목 집중(어텐션)’을 하도록 해 연산 정확도를 높임

트랜스포머 기반 모델들이 수학적 알고리즘과 같은 길이 일반화 문제에 어려움을 겪고 있음을 보여줍니다.(바닐라 어텐션과 비슷하게 제시되는 문제, 또한 포맷 및 정형화에 대한 이슈도 자주 언급됨) 이는 주로 모델이 입력 비트의 정확한 인덱스 기반 어드레스 지정에 실패하기 때문으로 추측되어지고 있습니다.

그러나 콘텐츠 기반 어드레스 지정을 활용하여 이 문제를 해결할 수 있는 방법을 제시하고, 특히 ‘기호(Mnemonics)’라는 도구를 사용하여 인덱스 기반 접근을 간접적으로 수행할 수 있도록 했습니다. (기호 및 앵커가 그 위치를 지정하는 역할을 함)

실험에서는 다양한 기호 형식을 사용하여 이진 패리티 작업과 다자리 덧셈 작업에서 모델의 길이 일반화 성능이 향상되었다고 보고하고 있으며 기호를 사용한 경우, 모델이 훈련 범위를 넘어서도 정확한 계산을 수행할 수 있었다고 합니다. 특히 중첩 스크래치패드 형식과 기호를 사용한 덧셈 작업에서 성능 향상을 관찰해 트랜스포머 모델들의 길이 일반화 문제를 해결하고, 모델이 더 복잡한 산술 작업과 알고리즘 작업에서도 일반화 능력을 향상시키기 위해 콘텐츠 기반 어드레스 지정을 보완하는 새로운 인덱스 기반 어드레스 지정 메커니즘을 통합하는 것이 바람직하다고 제안합니다.

1. 서론 (Introduction)

트랜스포머 기반 대규모 언어모델(LLM, Large Language Models)은 자연 언어 처리뿐만 아니라 다양한 지능형 작업에서 중추적인 역할을 수행합니다. 이 모델들은 코드 생성(Code Generation), 정리 증명(Theorem Proving), 다단계 인퍼런스(Multi-step Reasoning) 등 복잡한 작업을 수행할 수 있는 능력을 보유하고 있습니다. 그러나, 이와 같은 기능을 갖춘 모델들도 기본적인 산술 연산 같은 간단한 작업에서는 예상 외로 성능이 떨어지는 경우가 많습니다. 특히 길이 일반화(Length Generalization) 문제에서 약점을 드러내는데, 이는 훈련 중 보지 못한 길이의 문제를 해결하는 능력이 부족하기 때문입니다.

산술 작업은 목표가 명확하고 알고리즘 단계의 정확한 실행을 요구합니다. 이런 작업은 자연 언어 작업과 달리 각 토큰의 위치가 그 가치만큼 중요하며, 이는 자연어에서는 훨씬 유연한 의미와 구조를 가진다는 점에서 차별화됩니다.

예를 들어, “그는 쌍안경으로 고양이를 봤다”에서 “쌍안경으로”라는 표현은 문법적으로는 고양이에도 연결될 수 있지만 주로 “그”와 연결됩니다.

즉, 자연어 처리 작업에서는 토큰의 위치보다는 내용이 더 중요한 반면, 산술 작업에서는 각 토큰의 위치가 더 중요한 역할을 합니다. (어텐션 맵 등을 통해 확인)

2. 관련 연구 (Related Work)

길이 일반화는 트랜스포머 기반 시퀀스 모델에서 잘 알려진 문제로, 다양한 연구에서 이 문제를 다루고 있습니다. Anil et al. (2022)은 이진 패리티와 불리언 변수 할당 작업에서의 길이 일반화 능력을 탐구하였으며, 이런 작업에서도 모델이 일반화하는 데 어려움을 겪는다는 것을 발견하였습니다. 특히, Zhou et al. (2022)은 알고리즘 프롬프팅(Algorithmic Prompting)을 통해 모델이 작업을 학습할 때 인덱스 기반 접근 방식을 사용하도록 유도하는 새로운 방법을 제안했습니다. 또한, Kazemnejad et al. (2024)은 위치 인코딩 스키마를 사용하지 않는 것이 길이 일반화 문제를 더 잘 해결할 수 있음을 보여주었습니다. 이는 표준 위치 인코딩 방법이 인덱스 기반 어드레스 지정을 적절히 지원하지 못함을 시사합니다.

3. 랜덤 접근과 새로운 전략 (Random Accessing in LLMs – A Case Study)

이 섹션에서는 이진 패리티 작업을 통해 트랜스포머 기반 모델이 알고리즘 작업을 어떻게 학습하는지에 대한 사례 연구를 진행합니다. 이진 패리티 작업은 가장 기본적인 순차 산술 작업 중 하나로, 각 단계마다 하나의 비트 상태만을 전달하며 주로 XOR 연산을 학습하는 것이 필요합니다. 그러나 이런 모델은 훈련 중 보지 못한 길이의 시퀀스에 대해서 정확한 알고리즘을 학습하는 데 어려움을 겪습니다.

본 연구는 이진 패리티 작업을 통해 트랜스포머 모델이 길이 일반화를 어떻게 학습할 수 있는지를 심층적으로 탐구합니다. XOR 연산은 다음과 같이 정의됩니다.

\(\oplus\)는 XOR 연산자로 입력 비트가 서로 다를 때 1을 반환하며, 이는 두 비트의 ‘합’과 비슷하게 볼 수 있습니다.

모델이 이 연산을 올바르게 학습하려면 각 단계에서 현재 비트와 이전의 패리티를 정확히 식별하고 처리할 수 있어야 하는데, 이를 위해 ‘mnemonics’라는 새로운 전략을 도입하여 콘텐츠 기반 어드레스 지정을 인덱스 기반 어드레스 지정으로 변환하는 방법을 제안합니다.

스크래치패드의 사용

모델이 시퀀스의 패리티를 직접 출력해야 할 때, 트랜스포머는 생성된 각 토큰에 대해 고정된 계산을 수행하지만 문제의 크기는 변할 수 있습니다. 이는 모델이 단일 전달에서 전체 시퀀스에 대한 for-loop을 시뮬레이션해야 함을 의미합니다. 이 문제는 스크래치패드를 사용하여 해결할 수 있으며, 이를 통해 context window을 효과적으로 사용하여 for-loop을 명시적으로 시뮬레이션하고 중간 결과를 출력할 수 있습니다.

3.1 중첩 스크래치패드 (Interleaved Scratchpad)

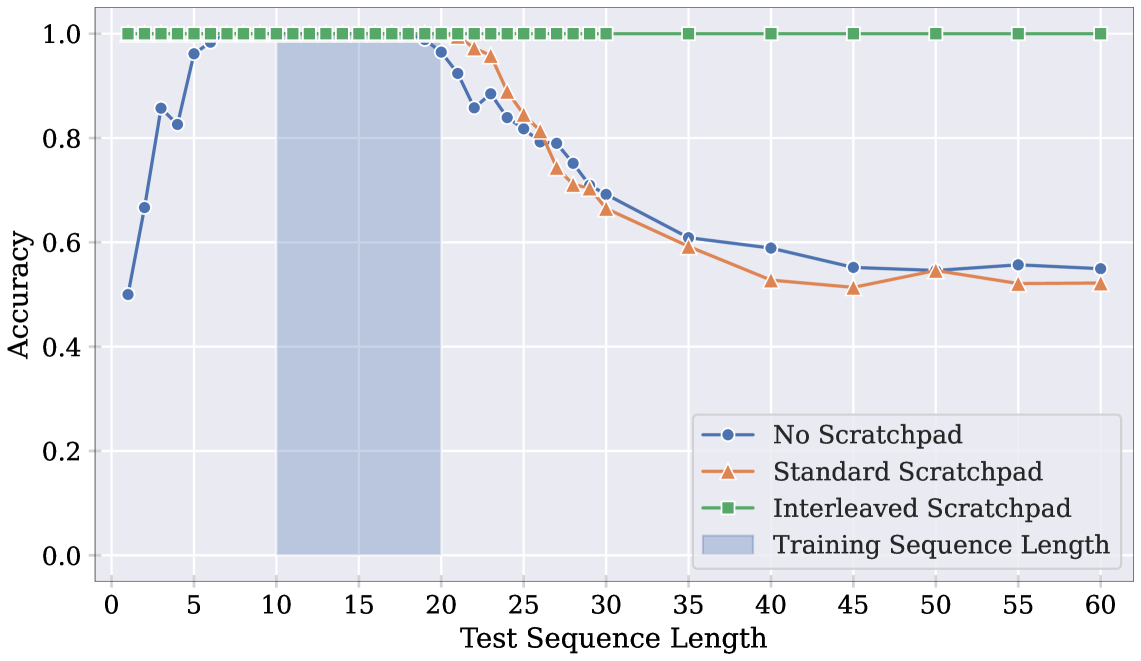
이진 패리티를 생성하기 위한 길이 일반화 솔루션은 세 단계로 구성됩니다. 1) 현재 활성 비트 읽기 2) 현재 실행 패리티 읽기 3) 활성 비트와 현재 패리티 간 XOR 수행

중첩 스크래치패드 형식에서는 시퀀스 비트와 실행 패리티가 번갈아 가며 배열되어, 각 단계에서 현재 활성 비트가 마지막 토큰이 되고, 현재 실행 패리티가 그 직전에 위치하게 됩니다. 이 배열은 첫 번째 단계를 크게 단순화시켜 모델이 길이 일반화 솔루션을 학습할 수 있게 합니다.

3.2 기호 (Mnemonics)

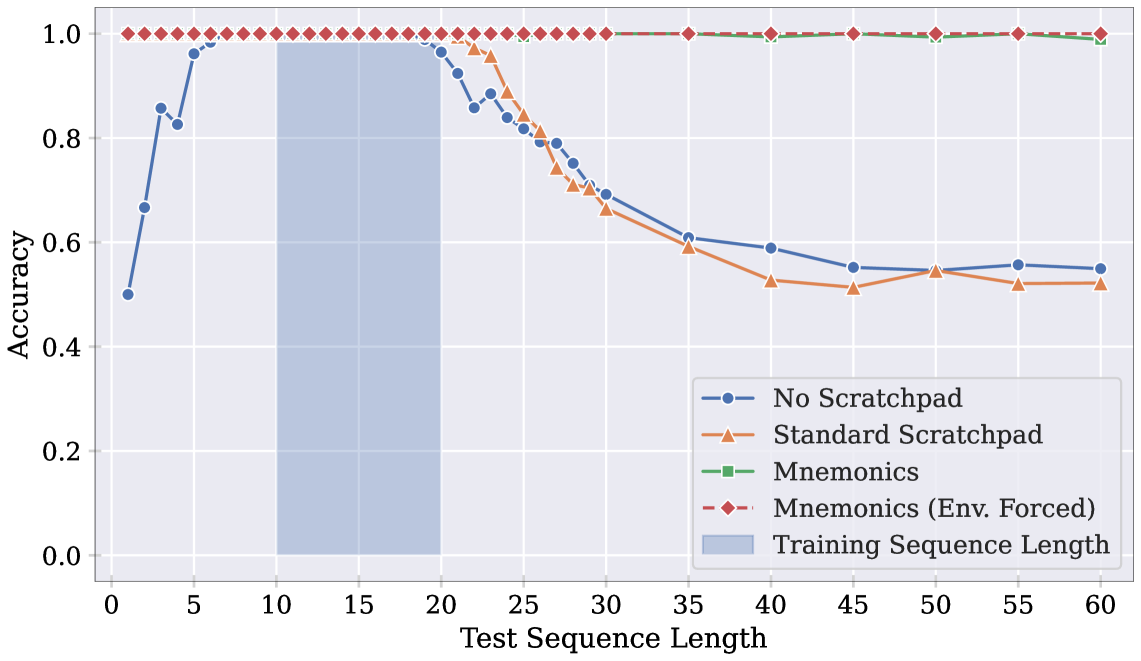
Figure 3

트랜스포머의 콘텐츠 기반 어드레스 지정 기능을 활용하여 인덱스 기반 어드레스 지정을 간접적으로 수행할 수 있습니다. 표준 스크래치패드 형식에 각 쌍의 해당 토큰 앞에 일치하는 “앵커” 토큰을 추가해 모델이 context window에서 이전 정보를 다시 방문할 수 있게 합니다. 이런 방식은 모델이 입력 시퀀스에서 일치하는 기호를 먼저 배치한 다음 각 단계에서 활성 비트를 어드레스 지정하는 데 사용됩니다.

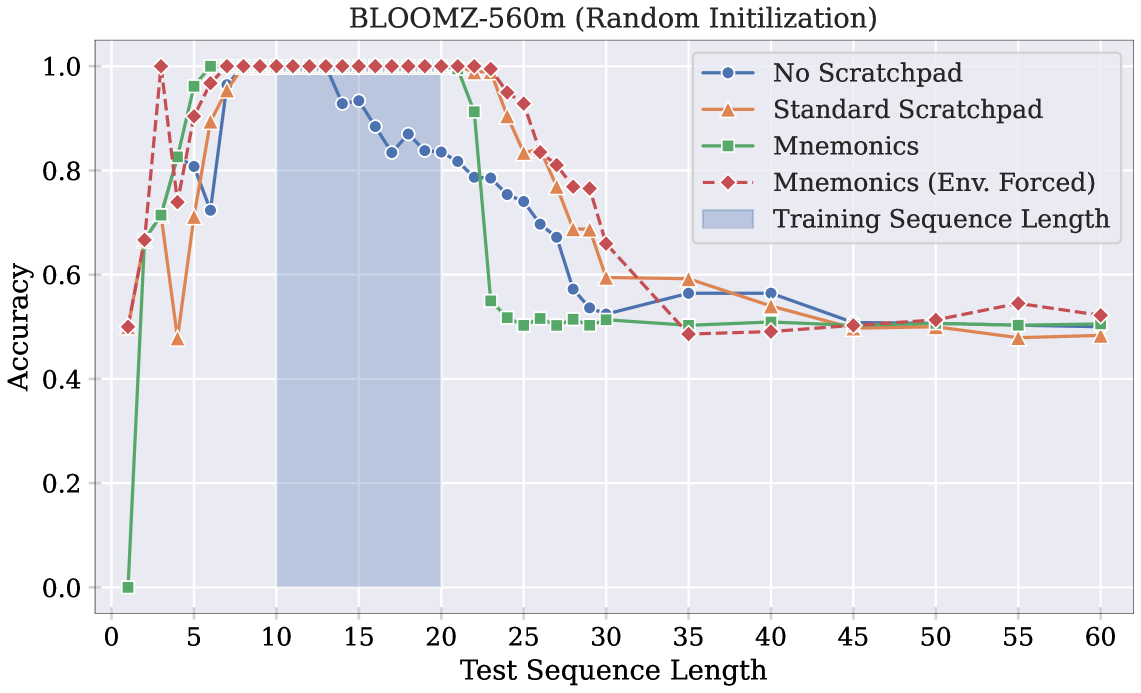
Figure 4

3.3 어텐션 패턴 분석 (Analysis of attention patterns)

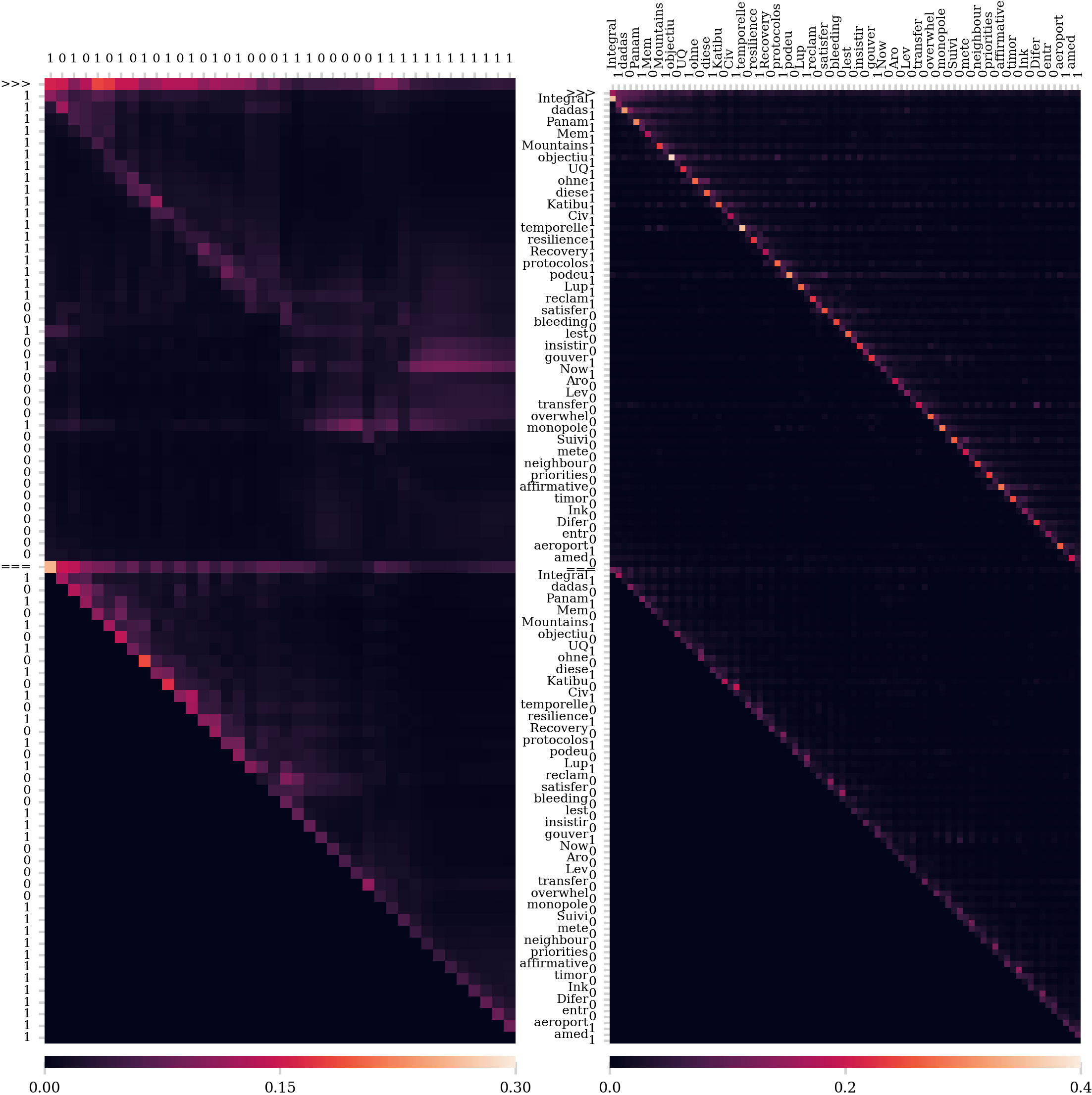
Figure 5

이 부분에서는 기호(Mnemonics) 사용 여부에 따라 모델의 어텐션 패턴이 어떻게 변화하는지 분석하기 위해 입력 기여도 시각화를 제시합니다. 이를 위해 그래디언트 × 입력 방법(Gradient × Input method)을 사용하여 전체 어텐션 맵을 시각화합니다. 이 맵은 출력 토큰을 열로, context window 내의 모든 토큰을 행으로 표시합니다. 모델의 작업은 입력 시퀀스의 실행 패리티를 생성하는 것이므로, 각 단계 \(i\)에서는 현재 비트(입력의 비트 \(i\))와 이전 실행 패리티(마지막으로 생성된 비트)만 주목해야 합니다. 이상적인 어텐션 맵은 이 두 관련 토큰을 나타내는 두 대각선 선을 보여줄 것입니다.

Figure 5는 10~20비트 길이로 훈련된 모델이 40비트 시퀀스의 패리티를 예측할 때, 기호 사용 유무에 따라 어텐션 패턴을 비교한 것입으로 기호 없이는 모델이 훈련 분포 내의 20비트 이후에 현재 비트를 정확히 주목하지 못하는 반면, 기호가 추가된 오른쪽 플롯에서는 훈련 범위를 넘어서도 거의 완벽한 어텐션 맵을 관찰할 수 있습니다.

어텐션 패턴 시각화 방법 색인마킹

3.4 기호 변형

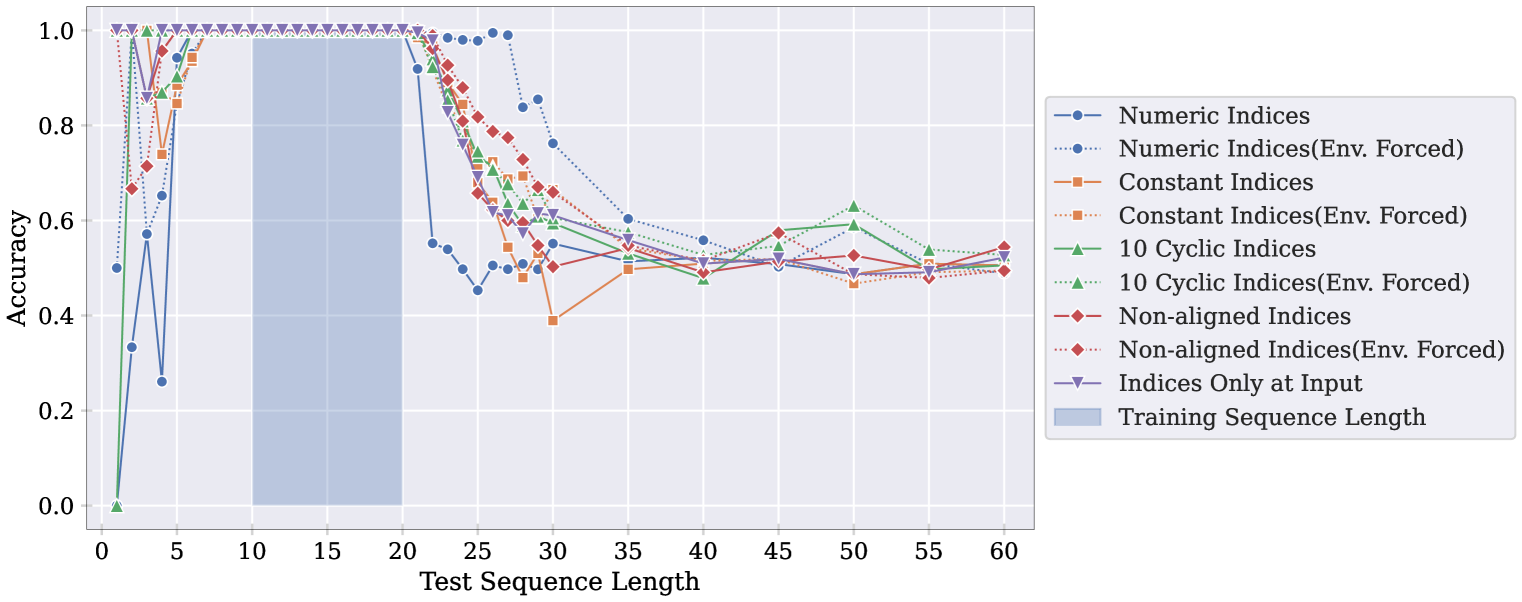
Figure 6

기호 토큰의 여러 변형을 실험하여 가설을 더욱 뒷받침합니다. 아래는 각 변형에 대한 설명입니다.

• 숫자 기호(Numeric Mnemonics): 연속적인 숫자 인덱스(1, 2, 3, …)를 모든 샘플에 대한 기호 토큰으로 사용합니다. 시퀀스 내의 이진 값과 혼동을 피하기 위해 비트를 나타내는 대신 'a', 'b'를 사용하며 이 형태의 기호는 절대 위치 인코딩에 해당합니다.
• 상수 기호(Constant Mnemonics): 단일 고정 문자(#)를 모든 샘플의 기호 토큰으로 사용합니다. 이 접근 방식은 기호의 효과가 어텐션 소모 현상(attention sink phenomenon)과 관련이 있는지, 아니면 모델이 중간 계산을 활성화에 저장하는 “플레이스홀더”로 기호 토큰을 사용하는지 테스트 합니다.
• 비정렬 기호(Non-aligned Mnemonics): 원래 기호와 비슷하지만 입력과 출력에서 사용된 무작위 토큰이 일치하지 않도록 변형합니다. 이 변형은 기호의 효과가 모델에게 각 자릿수를 고유하게 만드는 데 있다기보다는 위치 앵커 역할을 하는지 테스트하기 위해 사용됩니다.
• 순환 기호(Cyclic Mnemonics): 미리 정해진 기호 토큰 배열을 순환하면서 사용합니다. 훈련 및 테스트의 모든 샘플에서 고정된 기호를 사용합니다.

Figure 6은 이런 기호 변형을 사용하여 훈련된 BLOOMZ-560M 모델의 길이 일반화 성능을 보여줍니다. 환경 강제 버전에서는 모든 기호 토큰이 모델의 context window에 외부적으로 배치됩니다. 원래의 무작위 샘플링된 정렬된 기호와 비교할 때, 각 변형은 기호의 위치 앵커로서의 유틸리티를 손상시킵니다. 숫자 기호 변형에서는 훈련 중 노출된 기호 토큰(1, 2, …, 20) 외에 테스트 시 미처보지 못한 기호(21, 22, …)를 만나게 됩니다. 이는 훈련 예제 간의 고정된 기호 특성이 길이 일반화를 방해할 수 있음을 시사합니다.

이런 결과는 트랜스포머 모델이 무작위 토큰 접근을 수행하는 데 어려움을 겪고 있으며, 적절히 설계된 기호를 통해 이를 완화할 수 있음을 보여줍니다.

실험 결과

여러 트랜스포머 모델을 다양한 위치 인코딩 방법으로 파인튜닝하여, 10비트에서 20비트 길이의 작업 시퀀스에 대해 훈련시키고 최대 60비트 길이의 시퀀스에서 테스트했습니다. 기호를 사용한 스크래치패드는 모델이 정확한 알고리즘을 학습하고 완벽한 길이 일반화를 달성하는 데 도움이 되었습니다.

이런 결과는 모델이 산술 알고리즘을 정확하게 학습하는 데 있어 효과적인 인덱스 기반 어드레스 지정 메커니즘이 중요할 수 있음을 시사합니다. 또한, 환경 강제 버전이 아닌 기호를 사용하는 모델의 성능이 환경 강제 버전과 거의 동일하게 나타나, 모델이 기호를 효과적으로 배치하고 사용할 수 있음을 나타냅니다. 이런 결과는 기타 모델에서도 유사하게 보고되며, 기호 토큰 간 간격의 영향을 추가로 탐구하고 있습니다.

4. 여러 자리 덧셈 작업 해결 (Solving the Multi-digit Addition Task)

이 섹션에서는 여러 자리 덧셈 작업으로 연구 결과를 확장합니다. 이 작업은 다양한 스크래치패드 형식을 사용하여 문헌에서 광범위하게 탐구되었습니다. 본 연구에서는 세 가지 다른 형식의 기호를 사용하여 덧셈 작업의 길이 일반화 성능에 초점을 맞춥니다.

덧셈 형식

본 연구에서 사용된 형식에서, 덧셈 결과는 가장 작은 자릿수부터 가장 큰 자릿수까지 역순으로 초기 제시됩니다. 이후 모델은 ‘###’ 기호 뒤에 최종 덧셈 결과를 생성하기 위해 이를 뒤집습니다. 각 자릿수는 개별 토큰으로 변환됩니다. BLOOMZ-560M 모델을 이 형식을 사용하여 파인튜닝하였으며, 5자리에서 10자리 수에 대해 훈련을 시키고, 최대 14자리 수까지 테스트했습니다.

기호 사용 예

두 피연산자의 해당 자릿수에 동일한 기호를 사용했습니다.

• 기호 없음: >>> 1 2 + 9 === 1 2 0 ### 0 2 1
• 기호 사용: >>> M1 1 M2 2 M3 + M2 9 M3 === M2 1 M1 2 M3 0 ### M3 0 M1 2 M2 1
• 환경 강제: >>> M1 1 M2 2 M3 + M2 9 M3 === M2 1 M1 2 M3 0 ### M3 0 M1 2 M2 1

제로 패딩과 기호

피연산자를 제로 패딩하여 자릿수를 동일하게 맞춘 다음, 자릿수에 맞춰 기호를 삽입했습니다.

• 기호 없음: >>> 1 2 + 0 9 === 1 2 0 ### 0 2 1
• 기호 사용: >>> M1 1 M2 2 M3 + M1 0 M2 9 M3 === M2 1 M1 2 M3 0 ### M3 0 M1 2 M2 1
• 환경 강제: >>> M1 1 M2 2 M3 + M1 0 M2 9 M3 === M2 1 M1 2 M3 0 ### M3 0 M1 2 M2 1

비정렬 기호

두 피연산자의 해당 자릿수에 서로 다른 기호를 사용했습니다.

• 기호 없음: >>> 1 2 + 9 === 1 2 0 ### 0 2 1
• 기호 사용: >>> M1 1 M2 2 + M3 9 === M3 M2 1 M1 2 0 ### 0 M1 2 M3 M2 1
• 환경 강제: >>> M1 1 M2 2 + M3 9 === M3 M2 1 M1 2 0 ### 0 M1 2 M3 M2 1

성능 평가

Figure 7은 최대 14자리 수에 대한 덧셈 작업의 정확도를, 기호가 정렬된, 제로 패딩된, 비정렬된 형식으로 훈련되고 평가된 모델을 사용하여 보여줍니다. 예상대로, 정렬된 기호는 모델이 각 단계에서 올바른 자릿수를 선택하도록 안내합니다. 또한, 제로 패딩은 두 피연산자에 기호와 자릿수의 수를 동일하게 유지함으로써 작업 형식을 단순화합니다. 전반적으로, 이진 패리티 작업의 경우와 마찬가지로, 콘텐츠 기반 어드레스 지정을 활용하여 인덱스 기반 어드레스 지정을 가능하게 하는 기호를 사용함으로써, 트랜스포머 모델이 덧셈 작업에 대한 정확한 알고리즘을 성공적으로 학습할 수 있음을 보여줍니다.

5. 결론 (Conclusions)

트랜스포머 모델의 어텐션 메커니즘은 콘텐츠 기반 어드레스 지정에는 적합하지만, 알고리즘 인퍼런스 작업에서 중요한 랜덤 토큰 접근에는 어려움을 겪습니다. 이 연구는 인덱싱이 필요 없는 방법과 콘텐츠 기반 어드레스 지정을 통한 간접적인 랜덤 토큰 접근 방법의 효과를 보여주며, 이런 접근 방식이 모델이 알고리즘 작업에서 길이 일반화를 학습하는 데 도움이 될 수 있음을 시사합니다.