Mamba in the Llama

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-27

The Mamba in the Llama: Distilling and Accelerating Hybrid Models

• url: https://arxiv.org/abs/2408.15237
• pdf: https://arxiv.org/pdf/2408.15237
• abstract: Linear RNN architectures, like Mamba, can be competitive with Transformer models in language modeling while having advantageous deployment characteristics. Given the focus on training large-scale Transformer models, we consider the challenge of converting these pretrained models for deployment. We demonstrate that it is feasible to distill large Transformers into linear RNNs by reusing the linear projection weights from attention layers with academic GPU resources. The resulting hybrid model, which incorporates a quarter of the attention layers, achieves performance comparable to the original Transformer in chat benchmarks and outperforms open-source hybrid Mamba models trained from scratch with trillions of tokens in both chat benchmarks and general benchmarks. Moreover, we introduce a hardware-aware speculative decoding algorithm that accelerates the inference speed of Mamba and hybrid models. Overall we show how, with limited computation resources, we can remove many of the original attention layers and generate from the resulting model more efficiently. Our top-performing model, distilled from Llama3-8B-Instruct, achieves a 29.61 length-controlled win rate on AlpacaEval 2 against GPT-4 and 7.35 on MT-Bench, surpassing the best instruction-tuned linear RNN model.

TL;DR

효과적인 증류된 선형 (RNN + Mamba) architecture + Speculative decoding

• Transformer의 효율적 인퍼런스를 위한 선형 RNN으로의 변환 방법
• 사전 학습된 Transformer 가중치의 선형 RNN 매핑
• 추측적(예측적) 디코딩 등 Transformer 인퍼런스 기법의 새로운 아키텍처 적용

편의상 Speculative Decoding을 추측적(예측적) 디코딩으로 번역

선수 지식: Mamba, Transformers, SSM, Speculative Decoding, RNN

1. 서론

Transformer 아키텍처는 GPT, Llama, Mistral과 같은 대규모 언어모델의 성공을 이끌었지만, 시퀀스 길이에 대해 이차 복잡도를 가지며 큰 키-값(KV) 캐시가 필요하여 긴 시퀀스 생성에는 prohibitively 느립니다. 최근의 선형 RNN 모델들(Mamba, Mamba2, GLA, RetNet, Griffin)은 소규모에서 중규모의 통제된 실험에서 Transformer를 능가했지만, 최고의 Transformer 모델들은 여전히 downstream 작업에서 이런 모델들을 크게 앞서고 있습니다.

선형 RNN 모델의 주요 이점은 Transformer보다 더 빠른 인퍼런스(5배 높은 처리량)을 제공한다는 것입니다. 효율적인 인퍼런스은 LLM 시스템의 중요한 요구 사항으로 부상하고 있으며, 특히 다음과 같은 응용 분야에서 중요합니다.

1. 여러 개의 긴 문서나 대규모 코드베이스의 파일들에 대한 인퍼런스
2. 에이전트를 사용한 새로운 워크플로우에서 더 많은 궤적/경로(trajectory)를 탐색하고 복잡한 환경을 모델링하기 위한 대규모 배치 인퍼런스 및 긴 컨텍스트

이런 특성들을 효율적으로 생성하기 위해 대규모 사전 학습된 Transformer 모델을 선형 RNN으로 증류하는 것을 목표로 하며, 이를 해결하기 위해 다음 두 가지 기술적 과제를 해결하기 위한 방법을 제시합니다.

1. 증류를 위해 사전 학습된 Transformer 가중치를 선형 RNN 가중치로 매핑하는 방법
2. 추측적(예측적) 디코딩과 같은 최신 Transformer 인퍼런스 기법을 새로운 아키텍처에 적용하는 방법

위 두 가지 기술적 과제를 해결하기 위해 연구한 본 논문의 기여는 다음과 같습니다.

1. 어텐션 층의 가중치를 재사용하여 대규모 Transformer를 하이브리드-선형 RNN으로 변환하는 방법을 제시합니다. 이는 최소한의 추가 계산으로 생성 품질을 크게 유지하면서 가능합니다.
2. 점진적 증류, 지도 파인튜닝, 지시적 선호도 최적화를 결합한 다단계 증류 접근 방식을 제안합니다. 이 방법은 단순 증류에 비해 더 나은 펄플렉서티와 downstream 평가 결과를 보여줍니다.
3. Mamba와 하이브리드 아키텍처에 대한 하드웨어 인식 추측적(예측적) 샘플링 알고리즘과 빠른 커널을 개발합니다. 이를 통해 Mamba 7B 모델에 대해 초당 300개 이상의 토큰 처리량을 달성합니다.

실험에서는 Zephyr-7B, Llama-3 8B와 같은 다양한 대규모 오픈 채팅 LLM을 선형 RNN 모델(하이브리드 Mamba 및 Mamba2)로 증류합니다. 이 과정에서 단 20B 토큰의 훈련만을 사용합니다. 결과는 증류된 모델이 표준 채팅 벤치마크에서 teacher 모델과 대등한 성능을 보임을 나타냅니다. 또한, 1.2T 토큰으로 처음부터 훈련된 Mamba 7B 모델이나 3.5T 토큰으로 처음부터 훈련된 NVIDIA Hybrid Mamba2 모델을 포함한 유사한 크기의 모든 처음부터 사전 훈련된 Mamba 모델과 비교하여 여러 작업(e.g., MMLU, TruthfulQA)에서 대등하거나 더 나은 성능을 보입니다.

2. Transformer에서 Mamba로의 전환

2.1 어텐션과 선형 RNN의 관계

먼저 멀티헤드 어텐션을 검토하여 중간 객체의 형태를 명확히 하겠습니다. 표기법상 행렬 표현 대신 시퀀스 위치에 대한 명시적 첨자를 사용하여 두 모델 간의 유사성을 더 잘 강조하겠습니다.

어텐션은 여러 개의 서로 다르게 파라미터화된 헤드에 대해 병렬로 계산됩니다. 각 헤드는 히든 크기 $D$를 가진 시퀀스 $o$를 인수로 받아 다음과 같이 계산합니다.

$Q_t = W_Q o_t, K_t = W_K o_t, V_t = W_V o_t$ (모든 $t$에 대해)

$[\alpha_1 … \alpha_T] = \text{softmax} [Q_t^\top K_1 … Q_t^\top K_T] / \sqrt{D}$

상기 식에서 $o_t \in \mathbb{R}^{D \times 1}$, $y_t = \sum_{s=1}^T m_{s,t} \alpha_s V_s$, $W \in \mathbb{R}^{N \times D}$, $Q_t, K_t, V_t \in \mathbb{R}^{N \times 1}$, $m_{s,t} = \mathbb{1}(s \leq t)$입니다.

최근 연구에서는 선형 RNN이 대규모 언어모델에서 어텐션의 강력한 경쟁자가 될 수 있다고 주장했습니다. 유사한 공식을 가진 여러가지 선형 RNN 공식화가 제안되었습니다. 지금은 파라미터 $A_t, B_t, C_t$의 형태를 추상적으로 두고, 모든 선형 RNN이 다음과 같은 형태를 가진다는 점에 주목하겠습니다. (상기 식에서 $h$는 행렬 값을 가진 히든 스테이트)

$h_t = A_t h_{t-1} + B_t x_t$

$y_t = C_t h_t$

위와 같은 선형 RNN은 어텐션에 비해 여러가지 계산상의 이점을 가집니다.

1. 훈련 중에는 softmax 비선형성이 없기 때문에 모든 $y_t$ 값을 더 효율적으로 계산할 수 있고,
2. 인퍼런스 중에는 캐시를 필요로 하지 않으며, 각 다음에 등장할 토큰 $y_t$를 순차적으로 계산할 수 있습니다.

표면적으로 다른 형태임에도 불구하고, 선형 RNN과 어텐션 사이에는 자연스러운 관계가 있습으므로, softmax를 제거하여 어텐션 공식을 선형화하면 다음과 같습니다.

$ \begin{aligned} y_t &= \color{#FFB3BA}{\sum_{s=1}^T m_{s,t} \alpha_s V_s} &= \color{#BAFFC9}{\frac{1}{\sqrt{D}} Q_t \sum_{s=1}^T (m_{s,t} K_s^\top V_s)} &= \color{#BAE1FF}{\frac{1}{\sqrt{D}} Q_t \sum_{s=1}^T m_{s,t} K_s^\top W_V o_s} \end{aligned} $

• 원래의 어텐션 공식
• 어텐션에서 softmax를 제거해 선형화된 형태
• $V_s$를 $W_V o_s$로 확장한 형태

이제 이 선형화된 형태를 RNN 구조로 변환하면,

• $\color{#FFFFBA}{h_t}$: RNN의 히든 스테이트
• $\color{#FFD8BA}{y_t}$: RNN의 출력

위 변환된 형태는 표준 선형 RNN과 동일한 구조로 간주할 수 있습니다.

• $\color{#E0BAFF}{A_t = m_{t-1,t}}$
• $\color{#E0BAFF}{B_t = W_K}$
• $\color{#E0BAFF}{x_t = o_t}$
• $\color{#D1FFBA}{C_t = \frac{1}{\sqrt{D}} W_Q o_t}$

이렇게 변환함으로써, 선형화된 어텐션 메커니즘이 어떻게 선형 RNN 구조로 표현될 수 있는지 확인해보면, 결과적으로 표준 RNN 형태와 유사함을 확인할 수 있게 됩니다.

그러나 이렇게 변형된 버전은 $h \in \mathbb{R}^{N \times 1}$ 크기의 히든 스테이트를 사용해 각 은닉 차원에 대해 시간에 따라 하나의 스칼라만을 추적하기 때문에 이 변환을 그대로 적용하면 충분한 표현(representation)을 갖지 못하게 되어 모델 퍼포먼스가 떨어지게 됩니다. (어텐션에서 softmax의 비선형성이 중요하기 때문)

이런 모델을 개선하는 핵심은 더 긴 컨텍스트를 더 잘 포착하기 위해 선형 히든 스테이트의 capacity를 증가시키는 것으로 예를 들어, 이전 연구에서는 이 근사를 개선하기 위해 커널 방법을 사용했고, 커널 방법은 히든 스테이트 표현의 크기를 $h$에서 $\mathbb{R}^{N \times N’}$로 확장하여 softmax의 모델링 capacity를 더 잘 일치시키는 것으로 확인되었습니다.

[참고자료] 멀티헤드 어텐션 → 개선된 선형 RNN(히든 스테이트의 확장)

1. 멀티헤드 어텐션의 기본 구조

• $o_t \in \mathbb{R}^{D \times 1}$: 입력 시퀀스의 $t$ 번째 벡터
• $W_Q, W_K, W_V \in \mathbb{R}^{N \times D}$: 가중치 행렬
• $Q_t, K_t, V_t \in \mathbb{R}^{N \times 1}$: Query, Key, Value 벡터

멀티 헤드 어텐션에서 다음과 같이 어텐션 가중치를 계산하며,

최종 출력은 다음과 같습니다.

상기 식에서 $m_{s,t} = \mathbb{1}(s \leq t)$는 마스킹을 위한 지시함수

2. 선형 RNN의 기본 구조

($h_t$는 히든 스테이트, $x_t$는 입력, $y_t$는 출력)

3. 어텐션과 선형 RNN의 관계

상기 식은 다음과 같은 선형 RNN 형태로 변환될 수 있고,

이를 표준 선형 RNN 형태로 표현하면 다음과 같습니다.

• $A_t = m_{t-1,t}$
• $B_t = W_K o_t$
• $C_t = \frac{1}{\sqrt{D}} W_Q o_t$
• $x_t = W_V o_t$

예시로 이해하기

간단한 예시를 통해 이 변환을 살펴보겠습니다. $D=4$, $N=2$인 경우를 가정해봅시다.

입력 시퀀스 $o_t = [1, 2, 3, 4]^\top$에 대해

위와 같이 $Q_t, K_t, V_t$가 있다고 가정하겠습니다.

논문에서 제안한 개선 방안

이 변환의 주요 한계는 히든 스테이트 $h \in \mathbb{R}^{N \times 1}$의 크기가 작다는 것입니다. 이를 개선하기 위해 히든 스테이트의 크기를 $\mathbb{R}^{N \times N’}$로 확장할 수 있으며, softmax의 비선형성을 더 잘 근사할 수 있습니다. (표현력이 높아짐, 업데이트할 수 있는 파라미터 증가)

예를 들어, $N’ = 4$인 경우에는

이런 확장된 히든 스테이트를 사용해 $A_t, B_t, C_t$의 차원도 그에 맞게 capacity를 늘려야하고, 이런 방식으로 선형 RNN이 어텐션 메커니즘의 장점을 유지하면서도 계산 효율성을 개선할 수 있다고 언급합니다. (추후 mamba 블록으로 단계적으로 근사하기 위함)

코드로 이해하기

논문에 없는 섹션으로 구현이나 설명이 틀릴 수 있으므로 넘어가셔도 좋습니다.

멀티헤드 어텐션 및 RNN의 기본 구조를 살펴보고, 선형화된 어텐션과 선형화된 어텐션의 단점을 극복하기 위해 히든 스테이트의 사이즈를 늘리는 순서로 확인해보겠습니다. 이렇게 처리하면 계산 효율성과 메모리 capacity 개선으로 (Mamba의 가장 큰 장점인) 긴 시퀀스를 처리할 때의 이점이 두드러지지만, 모델의 표현력과 성능 사이의 균형을 잘 맞춰야만 합니다.

1. 멀티헤드 어텐션은 입력을 여러 개의 헤드로 나누어 병렬로 처리
2. 선형 RNN은 순차적으로 처리하며, 캐시된 상태는 유지
3. 선형화된 어텐션은 softmax를 제거해 계산은 단순화되지만, 성능 저하를 수반할 수 밖에 없으므로
4. 개선된 선형 RNN은 히든 스테이트의 크기를 확장하여 더 복잡한 표현을 학습할 수 있게 함. (히든 스테이트의 업데이트 capacity를 늘림)

2.1.1 멀티헤드 어텐션 기본 구조

import torch
import torch.nn as nn

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads
        
        # 1. Q, K, V를 위한 선형 변환 레이어 정의
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_o = nn.Linear(d_model, d_model)
        
    def forward(self, x):
        batch_size, seq_len, _ = x.size()
        
        # 2. 입력을 Q, K, V로 변환하고 헤드별로 분할
        q = self.W_q(x).view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
        k = self.W_k(x).view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
        v = self.W_v(x).view(batch_size, seq_len, self.num_heads, self.head_dim).transpose(1, 2)
        
        # 3. 어텐션 스코어 계산
        attn_scores = torch.matmul(q, k.transpose(-2, -1)) / (self.head_dim ** 0.5)
        # 4. 소프트맥스로 어텐션 확률 계산
        attn_probs = torch.softmax(attn_scores, dim=-1)
        
        # 5. 어텐션 가중치를 값(V)에 적용
        out = torch.matmul(attn_probs, v)
        # 6. 헤드 결과를 다시 합치고 원래 형태로 변환
        out = out.transpose(1, 2).contiguous().view(batch_size, seq_len, self.d_model)
        
        # 7. 최종 출력을 위한 선형 변환
        return self.W_o(out)

2.2.2 선형 RNN 기본 구조

class LinearRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        # 1. 가중치 행렬 초기화
        self.A = nn.Parameter(torch.randn(hidden_size, hidden_size))
        self.B = nn.Parameter(torch.randn(hidden_size, input_size))
        self.C = nn.Parameter(torch.randn(output_size, hidden_size))
        
    def forward(self, x):
        batch_size, seq_len, _ = x.size()
        # 2. 히든 스테이트 초기화
        h = torch.zeros(batch_size, self.A.size(0), device=x.device)
        outputs = []
        
        for t in range(seq_len):
            # 3. 히든 스테이트 업데이트
            h = torch.matmul(h, self.A.t()) + torch.matmul(x[:, t, :], self.B.t())
            # 4. 출력 계산
            y = torch.matmul(h, self.C.t())
            outputs.append(y)
        
        # 5. 모든 시간 단계의 출력을 스택으로 쌓아 반환
        return torch.stack(outputs, dim=1)

위 두가지(멀티헤드 어텐션, RNN) 기본 구조에서 어텐션을 선형화

2.2.3 선형화된 어텐션

어텐션을 선형화해서 선형 RNN 형태로 변환 (softmax를 제거해 계산은 단순화되지만, 성능 저하를 수반) → hidden state 더 필요해서 업데이트할 파라미터 늘려야 함.

class LinearizedAttention(nn.Module):
    def __init__(self, d_model):
        super().__init__()
        self.d_model = d_model
        # 1. Q, K, V를 위한 선형 변환 레이어 정의
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        
    def forward(self, x):
        batch_size, seq_len, _ = x.size()
        # 2. 히든 스테이트 초기화
        h = torch.zeros(batch_size, self.d_model, device=x.device)
        outputs = []
        
        for t in range(seq_len):
            # 3. 현재 입력에 대한 Q, K, V 계산
            q = self.W_q(x[:, t, :])
            k = self.W_k(x[:, t, :])
            v = self.W_v(x[:, t, :])
            
            # 4. 히든 스테이트 업데이트 (선형화된 어텐션)
            h = h + torch.matmul(k.unsqueeze(2), v.unsqueeze(1))
            # 5. 출력 계산
            y = torch.matmul(q.unsqueeze(1), h).squeeze(1) / (self.d_model ** 0.5)
            outputs.append(y)
        
        # 6. 모든 시간 단계의 출력을 스택으로 쌓아 반환 (본 논문에서의 히든 스테이트 1)
        return torch.stack(outputs, dim=1)

2.2.4 개선된 선형 RNN (확장된 히든 스테이트)

히든 스테이트의 capacity를 증가시켜 개선된 선형 RNN 구현 (히든 스테이트의 크기를 확장하여 더 복잡한 패턴을 포착할 수 있게 함)

class ImprovedLinearRNN(nn.Module):
    def __init__(self, d_model, hidden_expand):
        super().__init__()
        self.d_model = d_model
        self.hidden_expand = hidden_expand
        
        # 1. Q, K, V를 위한 선형 변환 레이어 정의
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        
        # 2. 확장된 히든 스테이트를 위한 가중치 행렬
        self.A = nn.Parameter(torch.randn(d_model, hidden_expand))
        # 3. 비선형성을 추가하기 위한 MLP
        self.mlp = nn.Sequential(
            nn.Linear(d_model, hidden_expand),
            nn.ReLU(),
            nn.Linear(hidden_expand, hidden_expand)
        )
        
    def forward(self, x):
        batch_size, seq_len, _ = x.size()
        # 4. 확장된 히든 스테이트 초기화
        h = torch.zeros(batch_size, self.d_model, self.hidden_expand, device=x.device)
        outputs = []
        
        for t in range(seq_len):
            # 5. 현재 입력에 대한 Q, K, V 계산
            q = self.W_q(x[:, t, :])
            k = self.W_k(x[:, t, :])
            v = self.W_v(x[:, t, :])
            
            # 6. MLP를 통한 비선형 변환
            delta = self.mlp(v)
            # 7. 확장된 히든 스테이트 업데이트
            h = torch.matmul(h, self.A) + torch.matmul(k.unsqueeze(2), delta.unsqueeze(1))
            # 8. 출력 계산
            y = torch.matmul(q.unsqueeze(1), h).squeeze(1) / (self.d_model ** 0.5)
            outputs.append(y)
        
        # 9. 모든 시간 단계의 출력을 스택으로 쌓아 반환
        return torch.stack(outputs, dim=1)

즉, 어텐션을 softmax를 제거해 계산을 단순화하면서 히든 스테이트까지 과하게 제거해버리면 너무 많은 정보의 생략이나 전달이 이루어지지 않을 수 있으므로, 히든 스테이트의 capacity를 늘려 해결하겠다는 아이디어인 것 같습니다. SSM 적용이 RNN에서 큰 이점을 갖을 수 있어서 그 쪽을 다시 살펴보려고 하는 것 같은데, transformers가 인퍼런스 시 무겁고, 비용이 많이 드는 것을 모두 다 인지한 상황에서 파라미터를 엄청나게 확장시켜보니 RNN보다 압도적인 퍼포먼스를 보여서 지금까지 온 것이기에… 앞으로 추가적으로 아이디어가 더 발전이 될 지 궁금하네요. 지금까지 후속 논문들을 보면 Mamba의 더 검토 의견이 합리적이였던 것 같기도….가장 처음에 제시 된 방향보다는 transformer와의 결합 혹은 증류 방식으로의 활용이 검토되는 것 같습니다. Anthropic처럼 파라미터 늘린 뉴런들의 representation을 분석하고, 규명해서 inferencetrajectory or 내부 인퍼런스 패스들을 정리하고, 보강해주는 것이 더 합리적이며 필요했던 방향성일지도…

결국 바닐라 어텐션의 단점을 SSM으로 해결해서 필요한 정보들만 빠르게 취사 선택한다는 것이 가장 큰 아이디어이므로 너무 많은 mamba 블록은 과도한 정보 생략과 문맥의 생략으로 이어질 수 있기 때문에 그것을 해결하기 위한 방안으로 제안하는 것 같습니다.

(개인적인 의견이므로 무시) 또, 현재의 트랜스포머 구조는 초기 레이어에 어텐션이 과하게 집중되는 현상이 있는데, Attention Sinks에서는 이것을 문제라고 지적했고, 탐구결과 및 레포지토리에서 추가 실험 결과 오히려 성능 저하가 관찰되었다고 하는데, 그것 역시 일정 포인트를 넘어가면 결국 contextual infomation 포착 및 요약 등 일부 태스크에 따라서는 앞 부분에 등장하는 시퀀스의 토큰이 중요하기 때문이지 않을까 싶습니다. 그것과 관련해서 조금 더 탐구한 논문이 나오지 않을까 싶습니다. 즉, 자연어에서 가장 초반에 오는 토큰들은 전체적인 맥락에서 큰 의미를 지닐 수 있으므로(두괄식 구성 혹은 핵심이 시퀀스에 앞 쪽에 주로 등장), mamba를 활용한 아키텍처 역시 이 부분에 대한 문제를 제대로 짚고 넘어가야하지 않을까 싶지만…

2.2 확장된 선형 RNN으로의 증류

효과적인 증류된 선형 RNN을 설계하기 위해, 원래 Transformer 파라미터를 최대한 가깝게 유지하면서도 선형 RNN의 capacity를 효율적으로 확장하는 것(본 논문의 핵심 접근방식)을 목표로 합니다. 원래의 어텐션 함수를 정확히 포착하려고 시도하지 않고, 대신 선형화된 형태를 증류의 시작점으로 사용합니다. (mamba 아키텍처의 특성상)

구체적으로, Mamba의 파라미터화를 적용하여 히든 스테이트 크기를 증가시키면서 어텐션 표현에서 초기화합니다. Mamba는 연속 시간 상태 공간 모델(SSM)을 사용하여 실행 시간에 선형 RNN을 파라미터화합니다. 이는 다음과 같은 미분 방정식으로 설명됩니다.

$h’(k) = Ah(k) + B(k)x(k)$

$y(k) = C(k)h(k)$

상기 식에서 $A$는 대각 행렬이고 다른 값들은 연속 신호입니다. 이 공식을 언어 모델링과 같은 이산 시간 문제에 적용하기 위해, 신경망을 사용하여 일련의 샘플링 간격 $\Delta t$와 이런 시간 단계에서의 신호 샘플을 생성합니다. 이런 샘플링 간격과 $B, C$의 $T$ 샘플이 주어지면, Mamba는 이산화로서 선형 RNN을 사용하여 연속 시간 방정식을 근사합니다.

이산 시간 형태를 나타내기 위해 오버바를 사용하여, 동적으로 재구성됩니다. 가장 간단한 경우, $N’ = 1$이고 항등 이산화를 사용하면 이 접근 방식은 앞서 논의한 선형 어텐션에서 선형 RNN으로의 변환을 복구합니다.

Mamba의 이점은 $N’ > 1$일 때 연속 시간 파라미터화를 통해 모델이 파라미터를 크게 늘리거나 효율성을 감소시키지 않고도 훨씬 더 풍부한 함수를 학습할 수 있다는 것입니다. 구체적으로, 유일한 추가 학습 파라미터는 샘플링 속도 $\Delta$와 동적 $A$입니다. 이 새로운 파라미터들은 이산화 함수를 통해 구성된 선형 RNN을 제어합니다.

구체적으로, 동일한 $B_t, C_t \in \mathbb{R}^{N \times 1}$와 $\Delta_t \in \mathbb{R}^{N’}$를 입력으로 받지만, $B_t, C_t \in \mathbb{R}^{N’ \times N \times 1}$를 출력해 효과적으로 은닉 크기를 단순한 선형 어텐션에 비해 $N’$ 배 증가시킵니다.

Mamba의 핵심 기여는 이 알고리즘의 하드웨어 인식 인수분해해서 보여주는 것으로, 알고리즘을 나이브하게 구현하면 새로 확장된 파라미터가 크기 때문에 느리지만, 이 접근 방식은 이산화, 상태 확장, 선형 RNN 적용을 단일 커널로 융합하여 이산 파라미터를 완전히 구체화하는 것을 우회해 상대적으로 비용 효율적으로 구성하고, 더 큰 $N’$을 사용할 수 있습니다.

코드로 이해하기

논문에 없는 내용으로 구현이나 설명이 틀릴 수 있으므로 넘어가셔도 좋습니다.

import torch
import torch.nn as nn
import torch.nn.functional as F

class AttentionInitializedMamba(nn.Module):
    def __init__(self, embed_size, num_heads, expand_size, seq_len):
        super().__init__()
        self.embed_size = embed_size
        self.num_heads = num_heads
        self.head_dim = embed_size // num_heads
        self.expand_size = expand_size
        self.seq_len = seq_len

        # 1. 어텐션 메커니즘을 위한 가중치 행렬
        self.W_k = nn.Linear(embed_size, embed_size)
        self.W_q = nn.Linear(embed_size, embed_size)
        self.W_v = nn.Linear(embed_size, embed_size)
        self.W_o = nn.Linear(embed_size, embed_size)
        
        # 2. 확장된 표현을 위한 MLP
        self.mlp = nn.Sequential(
            nn.Linear(self.head_dim, self.expand_size),
            nn.ReLU(),
            nn.Linear(self.expand_size, self.expand_size)
        )
        
        # 3. 상태 행렬 A 초기화
        self.A = nn.Parameter(torch.randn(num_heads, self.head_dim, expand_size))
        
        # 4. 이산화를 위한 추가 파라미터
        self.dt = nn.Parameter(torch.randn(expand_size))

    def disc(self, A, B, C, delta):
        # 5. 이산화 함수 구현
        # A_bar = (I + A * dt/2) / (I - A * dt/2)
        # B_bar = B * dt
        # C_bar = C
        I = torch.eye(A.shape[0], device=A.device)
        dt = F.softplus(self.dt)  # dt는 항상 양수여야 함
        A_bar = torch.matmul(I + A * dt.unsqueeze(0) / 2, 
                             torch.inverse(I - A * dt.unsqueeze(0) / 2))
        B_bar = B * dt.unsqueeze(0)
        C_bar = C
        return A_bar, B_bar, C_bar

    def linear_rnn(self, A, B, C, x):
        # 6. 선형 RNN 함수 구현
        batch_size = x.shape[0]
        h = torch.zeros(batch_size, self.expand_size, device=x.device)
        outputs = []
        
        for t in range(self.seq_len):
            h = torch.matmul(h, A.t()) + torch.matmul(x[:, t].unsqueeze(1), B.t())
            y = torch.matmul(h, C.t())
            outputs.append(y)
        
        return torch.stack(outputs, dim=1)

    def forward(self, o_t):
        batch_size = o_t.size(0)
        output = torch.zeros_like(o_t)

        for head in range(self.num_heads):
            # 7. 각 헤드에 대한 입력 변환
            x_t = self.W_v(o_t).view(batch_size, self.seq_len, self.num_heads, self.head_dim)[:, :, head]
            B_t = self.W_k(o_t).view(batch_size, self.seq_len, self.num_heads, self.head_dim)[:, :, head]
            C_t = self.W_q(o_t).view(batch_size, self.seq_len, self.num_heads, self.head_dim)[:, :, head]
            
            # 8. MLP를 통한 delta 계산
            delta_t = self.mlp(x_t)
            
            # 9. 이산화 함수 적용
            A_1_T, B_1_T, C_1_T = self.disc(self.A[head], B_t, C_t, delta_t)
            
            # 10. 선형 RNN 적용
            y = self.linear_rnn(A_1_T, B_1_T, C_1_T, x_t)
            
            # 11. 출력 누적
            output += self.W_o(y.view(batch_size, self.seq_len, -1))

        return output

2.3 어텐션-맘바 초기화 및 하이브리드 단계별 학습

이 섹션에서는 Transformer의 어텐션 메커니즘을 Mamba 구조로 변환하는 방법을 설명합니다. 알고리즘 1에서 제시된 접근 방식은 표준 Q, K, V 헤드를 Mamba 이산화에 직접 입력하고 결과적인 선형 RNN을 적용합니다.

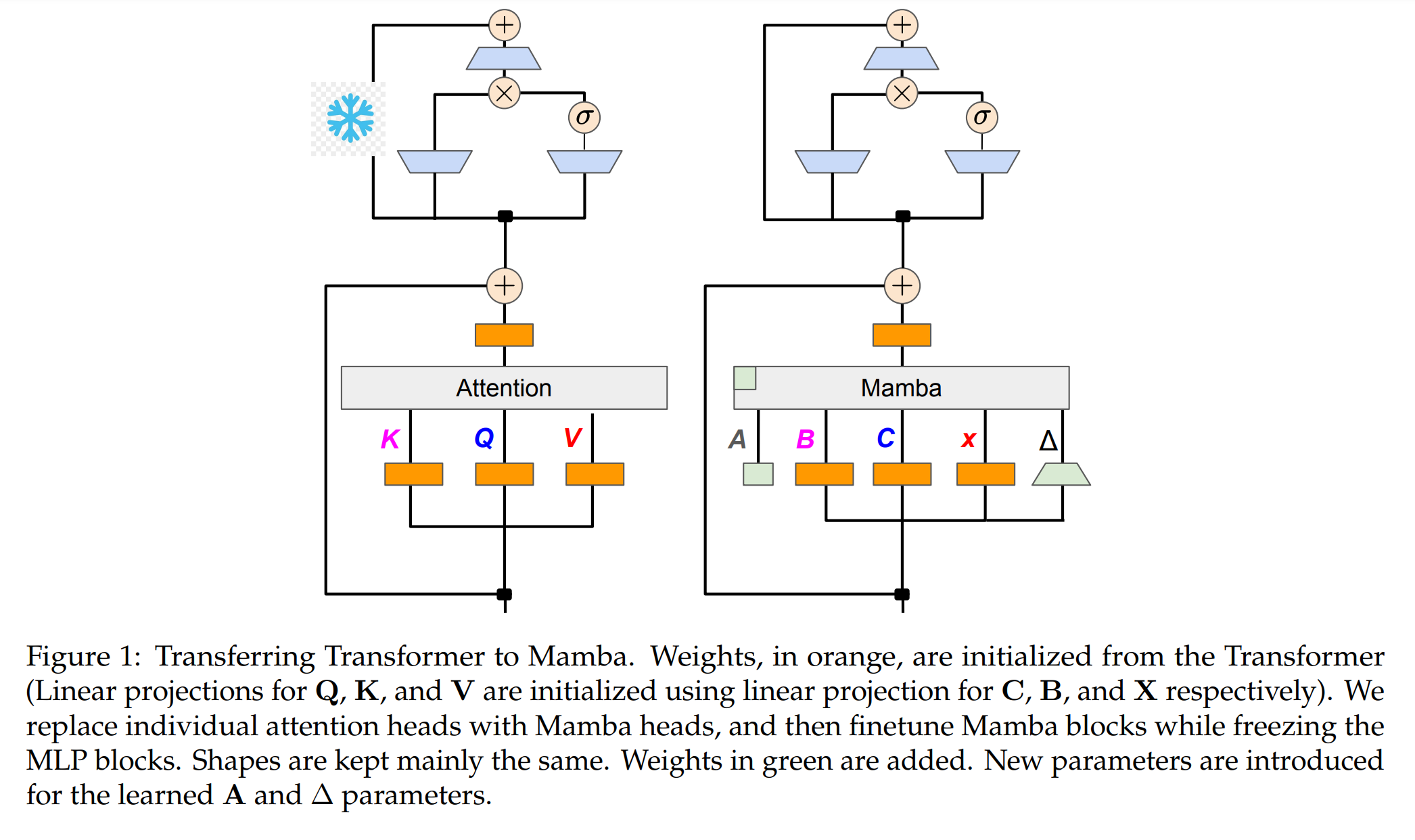
이 방법은 선형화된 어텐션으로 초기화하고 확장된 히든 스테이트를 통해 모델이 더 풍부한 상호작용을 학습할 수 있도록 합니다. Figure 1은 결과적인 아키텍처를 보여줍니다. 이 버전은 Transformer 어텐션 헤드를 직접 파인튜닝된 선형 RNN 레이어로 대체합니다. Transformer MLP 레이어는 그대로 유지하고 학습하지 않습니다.

이 접근 방식의 장점은 다음과 같습니다.

1. 어텐션 블록을 선형 RNN 블록으로 직접 대체할 수 있게 된다. (SSM으로 처리하는 것이 Context 윈도우 처리에 용이)
2. 그룹화된 쿼리 어텐션과 같은 추가 컴포넌트를 처리할 수 있다. (기존의 mamba 단일 아키텍처로는 어려웠다.)
3. 하이브리드 모델을 실험할 수 있어, $n$개의 어텐션 레이어마다 하나를 유지할 수 있다. (실험을 통해서 보고하였으나, 여러 조건에서 어떤 레이어에서의 임팩트를 확인하기 위한 절제 연구가 있었으면)

본 논문에서는 레이어를 단계적으로 대체하는 전략이 가장 효과적이라는 것을 경험적으로 발견했다고 보고합니다. 예를 들어, 먼저 2개의 레이어마다 하나를 유지하고 증류한 다음, 4개마다 하나를 유지하는 방식으로 점차적으로 mamba 아키텍처로의 증류를 계속하는 것이 더 좋았다고 합니다.

1. 선형화된 어텐션 공식 \(y_t = \frac{1}{\sqrt{D}}Q_t \sum_{s=1}^t m_{s,t}K_s^T W_V o_s\)

2. 선형 RNN 형태로의 변환 \(h_t = m_{t-1,t}h_{t-1} + K_t V_t\)

   \[y_t = \frac{1}{\sqrt{D}}Q_t h_t\]

3. Mamba의 연속 시간 상태 공간 모델 (SSM) \(h'(k) = Ah(k) + B(k)x(k)\)

   \[y(k) = C(k)h(k)\]

4. 이산화된 Mamba 모델 \(A_{1...T}, B_{1...T}, C_{1...T} = \text{Discretize}(A, B_{1...T}, C_{1...T}, \Delta_{1...T})\)

이런 수학적 변환을 통해, Transformer의 어텐션 메커니즘을 Mamba의 선형 RNN 구조로 효과적으로 매핑할 수 있으며, 모델의 인퍼런스 속도를 크게 향상시키면서도 원래 Transformer의 성능을 유지할 수 있다고 언급합니다.

이 방법의 핵심은 어텐션 메커니즘의 선형화된 형태를 초기 지점으로 사용하고, Mamba의 확장된 히든 스테이트를 통해 더 제대로 표현(representation)을 학습할 수 있도록 하는 것으로 이는 기존 Transformer 모델의 가중치를 최대한 활용하면서도, 선형 RNN의 계산 효율성을 얻을 수 있는 접근 방식이라고 언급합니다.

실험적으로, 이 방법을 사용해본 결과 연구팀은 단계적 대체 전략을 통해 가장 효과적인 결과를 얻었다고 하며, 이는 모델이 점진적으로 새로운 구조에 적응할 수 있게 하며, 성능 저하를 최소화하면서 효율성을 개선할 수 있음을 시사합니다. (단계별 증류)

코드로 이해하기 점진적으로 Mamba 구조 적응 (경험적으로 가장 좋았다고 보고)

논문에 없는 내용으로 구현이나 설명이 틀릴 수 있으므로 넘어가셔도 좋습니다.

어텐션 레이어의 가중치를 사용하여 Mamba 블록을 초기화하고, 하이브리드 모델에서 어텐션과 Mamba 블록을 혼합하여 사용하는 구조

2.3.1 기본 Mamba 블록 구현

Mamba의 핵심 구성 요소인 상태 공간 모델(SSM) (약식 구현체)

import torch
import torch.nn as nn

class SSM(nn.Module):
    def __init__(self, d_model, d_state):
        super().__init__()
        self.d_model = d_model
        self.d_state = d_state
        
        # 1. SSM 파라미터 초기화
        self.A = nn.Parameter(torch.randn(d_model, d_state, d_state))
        self.B = nn.Parameter(torch.randn(d_model, d_state, 1))
        self.C = nn.Parameter(torch.randn(d_model, 1, d_state))
        self.D = nn.Parameter(torch.randn(d_model, 1, 1))
        
    def forward(self, u):
        # u: (batch_size, seq_len, d_model)
        batch_size, seq_len, _ = u.shape
        
        # 2. 초기 상태와 출력 텐서 초기화
        x = torch.zeros(batch_size, self.d_model, self.d_state, device=u.device)
        y = torch.zeros(batch_size, seq_len, self.d_model, device=u.device)
        
        # 3. 시퀀스를 따라 SSM 계산
        for t in range(seq_len):
            # 4. 상태 업데이트
            x = torch.einsum('bdi,bio->bdo', x, self.A) + self.B * u[:, t, :].unsqueeze(-1)
            # 5. 출력 계산
            y[:, t, :] = (torch.einsum('bdi,boi->bdo', x, self.C) + self.D * u[:, t, :].unsqueeze(-1)).squeeze(-1)
        
        return y

2.3.2 Mamba 블록 구현

SSM을 포함하는 전체 Mamba 블록 (약식 구현체)

class MambaBlock(nn.Module):
    def __init__(self, d_model, d_state, d_conv=4):
        super().__init__()
        self.d_model = d_model
        self.d_state = d_state
        
        # 1. Mamba 블록 컴포넌트 초기화
        self.in_proj = nn.Linear(d_model, d_model * 2)
        self.conv = nn.Conv1d(d_model, d_model, kernel_size=d_conv, padding=d_conv-1, groups=d_model)
        self.act = nn.SiLU()
        self.ssm = SSM(d_model, d_state)
        self.out_proj = nn.Linear(d_model, d_model)
        
    def forward(self, x):
        # x: (batch_size, seq_len, d_model)
        residual = x
        # 2. 입력 프로젝션 및 게이트 분리
        x, gate = self.in_proj(x).chunk(2, dim=-1)
        
        # 3. 컨볼루션 적용
        x = x.transpose(1, 2)
        x = self.conv(x)[:, :, :x.size(-1)]
        x = x.transpose(1, 2)
        
        # 4. 활성화 함수 적용
        x = self.act(x)
        # 5. SSM 적용
        x = self.ssm(x)
        # 6. 게이트 적용
        x = x * gate
        
        # 7. 출력 프로젝션 및 잔차 연결
        return self.out_proj(x) + residual

2.3.3 어텐션 초기화된 Mamba 구현

어텐션 가중치로 초기화된 Mamba 블록 (약식 구현체)

class AttentionInitializedMamba(nn.Module):
    def __init__(self, d_model, num_heads, d_state):
        super().__init__()
        self.d_model = d_model
        self.num_heads = num_heads
        self.head_dim = d_model // num_heads
        
        # 1. 어텐션 가중치 초기화
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        
        # 2. Mamba 블록 초기화
        self.mamba = MambaBlock(d_model, d_state)
        
    def initialize_from_attention(self, attention_layer):
        # 3. 어텐션 레이어로부터 가중치 초기화
        self.W_q.weight.data = attention_layer.W_q.weight.data
        self.W_k.weight.data = attention_layer.W_k.weight.data
        self.W_v.weight.data = attention_layer.W_v.weight.data
        
    def forward(self, x):
        # 4. Q, K, V 계산
        q = self.W_q(x)
        k = self.W_k(x)
        v = self.W_v(x)
        
        # 5. QKV 연결 및 Mamba 블록 적용
        qkv = torch.cat([q, k, v], dim=-1)
        return self.mamba(qkv)

2.4.4 하이브리드 모델 구현

어텐션과 Mamba를 혼합한 하이브리드 모델 (약식 구현체)

class HybridTransformerMamba(nn.Module):
    def __init__(self, d_model, num_heads, num_layers, d_state, mamba_ratio=0.5):
        super().__init__()
        self.d_model = d_model
        self.num_layers = num_layers
        
        # 1. 레이어 초기화
        self.layers = nn.ModuleList()
        for i in range(num_layers):
            # 2. Mamba와 Transformer 레이어 번갈아 추가
            if i % 2 == 0 and i / num_layers < mamba_ratio:
                self.layers.append(AttentionInitializedMamba(d_model, num_heads, d_state))
            else:
                self.layers.append(nn.TransformerEncoderLayer(d_model, num_heads))
        
    def forward(self, x):
        # 3. 모든 레이어를 순차적으로 적용
        for layer in self.layers:
            x = layer(x)
        return x

2.4.5 단계별 학습 구현

단계별 학습을 위한 함수 (약식 구현체)

def staged_training(model, train_dataloader, num_epochs, mamba_ratios):
    # 1. 옵티마이저와 손실 함수 초기화
    optimizer = torch.optim.Adam(model.parameters())
    criterion = nn.CrossEntropyLoss()
    
    for ratio in mamba_ratios:
        print(f"Training with Mamba ratio: {ratio}")
        # 2. Mamba 비율 설정
        model.set_mamba_ratio(ratio)
        
        for epoch in range(num_epochs):
            for batch in train_dataloader:
                # 3. 배치 학습
                optimizer.zero_grad()
                inputs, targets = batch
                outputs = model(inputs)
                loss = criterion(outputs, targets)
                loss.backward()
                optimizer.step()
            
            print(f"Epoch {epoch+1}/{num_epochs}, Loss: {loss.item()}")
        
    return model

model = HybridTransformerMamba(d_model=512, num_heads=8, num_layers=12, d_state=16)
mamba_ratios = [0.25, 0.5, 0.75]
trained_model = staged_training(model, train_dataloader, num_epochs=5, mamba_ratios=mamba_ratios)

[참고자료] SSM의 적용과 RNN과 Transformers와의 비교

1. SSM의 기본 수식

SSM은 연속 시간 상태 공간 모델로, 다음과 같은 미분 방정식으로 표현됩니다.

• $h(t)$: 히든 스테이트 벡터
• $x(t)$: 입력 벡터
• $y(t)$: 출력 벡터
• $A$, $B$, $C$: 모델 파라미터

2. 이산화 과정

연속 시간 모델을 이산 시간 모델로 변환하기 위해, 다음과 같은 이산화 과정을 거칩니다.

• $\bar{A} = e^{A\Delta t}$
• $\bar{B} = A^{-1}(e^{A\Delta t} - I)B$
• $\Delta t$: 시간 간격

3. Python 코드 구현

import numpy as np
from scipy.linalg import expm

class SSM:
    def __init__(self, A, B, C, delta_t):
        self.A = A
        self.B = B
        self.C = C
        self.delta_t = delta_t
        
        # 이산화된 파라미터 계산
        self.A_bar = expm(A * delta_t)  # (1) e^(A*delta_t)
        self.B_bar = np.linalg.inv(A) @ (expm(A * delta_t) - np.eye(A.shape[0])) @ B  # (2) A^(-1)(e^(A*delta_t) - I)B

    def forward(self, x):
        T = len(x)
        d = self.A.shape[0]
        h = np.zeros((T+1, d))
        y = np.zeros((T, self.C.shape[0]))
        
        for t in range(T):
            h[t+1] = self.A_bar @ h[t] + self.B_bar @ x[t]  # (3) h_{t+1} = A_bar * h_t + B_bar * x_t
            y[t] = self.C @ h[t]  # (4) y_t = C * h_t
        
        return y


A = np.array([[-0.1, 0.5], [-0.5, -0.1]])
B = np.array([[1.0], [0.5]])
C = np.array([[1.0, 0.0]])
delta_t = 0.1

ssm = SSM(A, B, C, delta_t)

# 입력 시퀀스
x = np.random.randn(100, 1)

# 모델 출력 계산
y = ssm.forward(x)

• 연속 시간 모델 정의: 식 (1)과 (2)로 SSM을 정의
• 이산화: 연속 시간 모델을 이산 시간 모델로 변환 (식 3, 4).
• 파라미터 계산: $\bar{A}$와 $\bar{B}$를 계산
• 순전파: 입력 시퀀스에 대해 상태를 갱신하고 출력을 생성

4. 기존 방식(RNN, Transformer)과의 차이점

• RNN과의 차이
  • SSM은 연속 시간 모델을 기반으로 하며, 이를 이산화하여 사용합니다.
  • RNN은 처음부터 이산 시간 모델로 설계되었습니다.
  • SSM은 상태 전이를 미분 방정식으로 모델링하여 더 풍부한 state를 표현할 수 있습니다.
• Transformer와의 차이
  • SSM은 선형적인 상태 전이를 사용하여 긴 시퀀스를 효율적으로 처리할 수 있습니다.
  • Transformer는 Self-attention 메커니즘을 사용하여 비선형적인 관계를 포착하지만, 긴 시퀀스에서는 계산 복잡도가 높아집니다.
  • SSM은 $O(T)$의 시간 복잡도를 가지는 반면, Transformer는 $O(T^2)$의 복잡도를 가집니다.

코드

# (1) A_bar 계산: e^(A*delta_t)
self.A_bar = expm(A * delta_t)

# (2) B_bar 계산: A^(-1)(e^(A*delta_t) - I)B
self.B_bar = np.linalg.inv(A) @ (expm(A * delta_t) - np.eye(A.shape[0])) @ B

# (3) 상태 갱신: h_{t+1} = A_bar * h_t + B_bar * x_t
h[t+1] = self.A_bar @ h[t] + self.B_bar @ x[t]

# (4) 출력 계산: y_t = C * h_t
y[t] = self.C @ h[t]

위에서 설명한 것처럼 SSM(State Space Model) 구조는 긴 시퀀스를 효율적으로 처리할 수 있으며, 연속적인 시간을 이산적인 시간 모델로 근사(이산화)하여 표현력과 계산 효율성 간의 균형을 맞추려는 시도 중 하나입니다.

The SSM (State Space Model) structure can efficiently process long sequences, and it is one of the attempts to balance expressiveness and computational efficiency by approximating continuous-time dynamics with discrete-time models.

3. 정렬된 언어 모델을 위한 지식 증류

지식 증류(KD)는 큰 teacher 네트워크의 행동을 모방하는 더 작은 네트워크를 훈련시키는 압축 기술입니다. Transformer 파라미터로 모델을 초기화한 후, 원래 언어 모델과 대등한 성능을 내도록 이를 증류하는 것을 목표로 합니다. Transformer의 대부분의 지식이 원래 모델에서 전이된 MLP 레이어에 유지되어 있다고 가정하고, LLM의 파인튜닝 및 정렬 단계를 증류하는 데 집중합니다. 이 단계에서 MLP 레이어는 고정되고 Mamba 레이어는 Figure 1과 같이 훈련됩니다.

• 지식 증류를 통한 Transformer에서 Mamba로의 모델 압축
• 지도 학습 파인튜닝과 선호도 최적화를 결합한 다단계 증류 방법
• 직접 선호도 최적화(DPO)를 증류 목적함수로 활용한 새로운 접근

지도 학습 파인튜닝(SFT)

먼저 언어 모델 적응의 지도 학습 파인튜닝(SFT) 단계를 재수행하기 위해 지식 증류를 적용합니다. 이 단계에서 LLM은 입력 프롬프트 $x$가 주어졌을 때 응답 $y$의 가능성을 최대화하도록 훈련됩니다, 즉 $p(y\|x)$를 최대화합니다. 이 작업은 조건부 생성과 유사합니다.

이 설정에서 증류를 위한 두 가지 일반적인 접근 방식이 있습니다.

1. 단어 수준 KL-발산 사용 student 모델 $p(\cdot;\theta)$의 전체 확률 분포를 teacher 모델 $p(\cdot;\theta_T)$의 전체 분포와 일치시키기 위해 위치 $t$에서 다음 가능한 토큰 전체 집합에 대한 KL Divergence을 최소화합니다.

2. 시퀀스 수준 지식 증류(SeqKD) SeqKD는 이런 스타일의 작업에 대한 간단한 증류 방법을 제안합니다. 실제 텍스트 $y_{1\cdots t}$를 teacher 생성 출력 $\hat{y}_{1\cdots t}$(의사 레이블이라고도 함)로 대체합니다.

손실 함수는 다음과 같이 정의됩니다.

상기 식에서 $\theta$는 student 모델의 학습 가능한 파라미터이고, $\alpha$와 $\beta$는 각각 시퀀스 손실과 단어 손실 항의 가중치를 제어합니다.

선호도 최적화(Preference Optimization, PO)

LLM의 지시 조정의 두 번째 단계는 일련의 사용자 선호도에 맞추는 것입니다. 이 단계에서는 원하는 선호도 쌍 집합을 사용하여 모델의 출력을 개선합니다. 목표는 보상 모델 $r$을 최대화하면서 Baseline Model에 가까운 프롬프트 $x$에 대한 출력 $y$를 생성하는 것입니다. 일반적으로 Baseline Model은 지도 학습 파인튜닝 후의 모델로 선택됩니다.

1. 효율적인 모델 압축: Transformer에서 Mamba로의 변환을 통해 모델 크기를 줄이면서도 성능을 유지합니다.
2. 다단계 증류: 지도 학습 파인튜닝과 선호도 최적화를 결합하여 더 효과적인 증류 과정을 구현합니다.
3. 새로운 증류 목적함수: DPO를 증류에 활용함으로써 더 효과적인 학습이 가능해집니다.

증류를 위해 편리하게 원래의 teacher를 활용할 수 있습니다.

상기 식에서 보상 함수 $r_\phi(x,y)$는 사용된 방법에 따라 다릅니다. 이전 연구에서는 주로 근접 정책 최적화(PPO)와 같은 강화 학습 방법을 사용하여 이 보상에 관한 $\phi$를 최적화했습니다.

최근에는 직접 선호도 최적화(DPO) 방법이 직접적인 그래디언트 업데이트를 통해 이 목적함수를 효과적으로 최적화하는 데 사용되었습니다. 구체적으로, DPO는 주어진 프롬프트 $x$에 대해 선호되는 출력 $y_w$와 선호되지 않는 출력 $y_l$에 접근할 수 있다면, 이 최적화 문제를 다음과 같이 재구성할 수 있음을 보여줍니다.

이 최적화는 teacher와 student의 선호되는 출력과 선호되지 않는 출력을 시퀀스 수준에서 점수화한 다음 student에게 역전파하여 수행할 수 있습니다. 아는 한, 이것은 DPO를 증류 목적함수로 사용한 최초의 사례입니다.

이 방법은 대규모 언어모델의 효율적인 압축과 정렬을 동시에 달성할 수 있는 새로운 접근 방식을 제시하며, DPO를 증류 과정에 도입한 것은 지금까지 거의 처음 나온 형태인 것 같습니다.

[참고자료] KD(Knowledge Distillation), SFT(Supervised Fine-Tuning), PO(Preference Optimization)

1. 지식 증류 (Knowledge Distillation, KD)
   • 큰 teacher 네트워크의 행동을 모방하는 작은 student 네트워크를 훈련
   • Transformer 파라미터로 초기화 후, 원래 LM과 동등한 성능을 내도록 증류
   • 가정: Transformer의 지식 대부분이 MLP 층에 유지됨
   • 과정: MLP 층은 고정하고 Mamba 층만 훈련
2. 지도 파인튜닝 (Supervised Fine-Tuning, SFT)
   • 입력 프롬프트 x에 대한 응답 y의 확률 \(p(y\\|x)\) 최대화
   • 방법 1: 단어 수준 KL-Divergence 최소화
   • 방법 2: 시퀀스 수준 지식 증류 (SeqKD)
     • 실제 텍스트 대신 teacher 모델의 생성 출력(의사 레이블) 사용
   • 손실 함수: \(L(\theta) = -\sum_{t=1}^T \alpha \log p(\hat{y}_{t+1} \\| \hat{y}_{1:t}, x, \theta) + \beta KL[p(\cdot \\| \hat{y}_{1:t}, x, \theta_T) \\|\\| p(\cdot \\| \hat{y}_{1:t}, x, \theta)]\) $\theta$는 student 모델의 학습 가능한 파라미터, $\alpha$와 $\beta$는 시퀀스 및 단어 손실 항의 가중치
3. 선호도 최적화 (Preference Optimization)
   • 사용자 선호도에 맞는 출력 생성
   • 보상 모델 r을 최대화하면서 Baseline Model(SFT 후 모델)과 가까이 유지
   • 목적함수 \(\max_{\theta} \mathbb{E}_{x\sim D, y\sim p(y\\|x;\theta)} [r_\phi(x,y) - \beta KL[p(y\\|x;\theta) \\|\\| \pi(y\\|x;\theta_T)]]\)
   • 직접 선호도 최적화 (Direct Preference Optimization, DPO) 사용 \(\pi_\theta = \max_{\theta} \mathbb{E}_{(x,y_w,y_l) \sim D} \left[\log \sigma\left(\beta\log \frac{p(y_w\\|x;\theta)}{p(y_w\\|x;\theta_T)} - \beta\log \frac{p(y_l\\|x;\theta)}{p(y_l\\|x;\theta_T)}\right)\right]\) $y_w$는 선호되는 출력, $y_l$은 선호되지 않는 출력

4. 선형 RNN을 위한 추측적(예측적) 디코딩 알고리즘 (Speculative Decoding Algorithms For Linear RNNs)

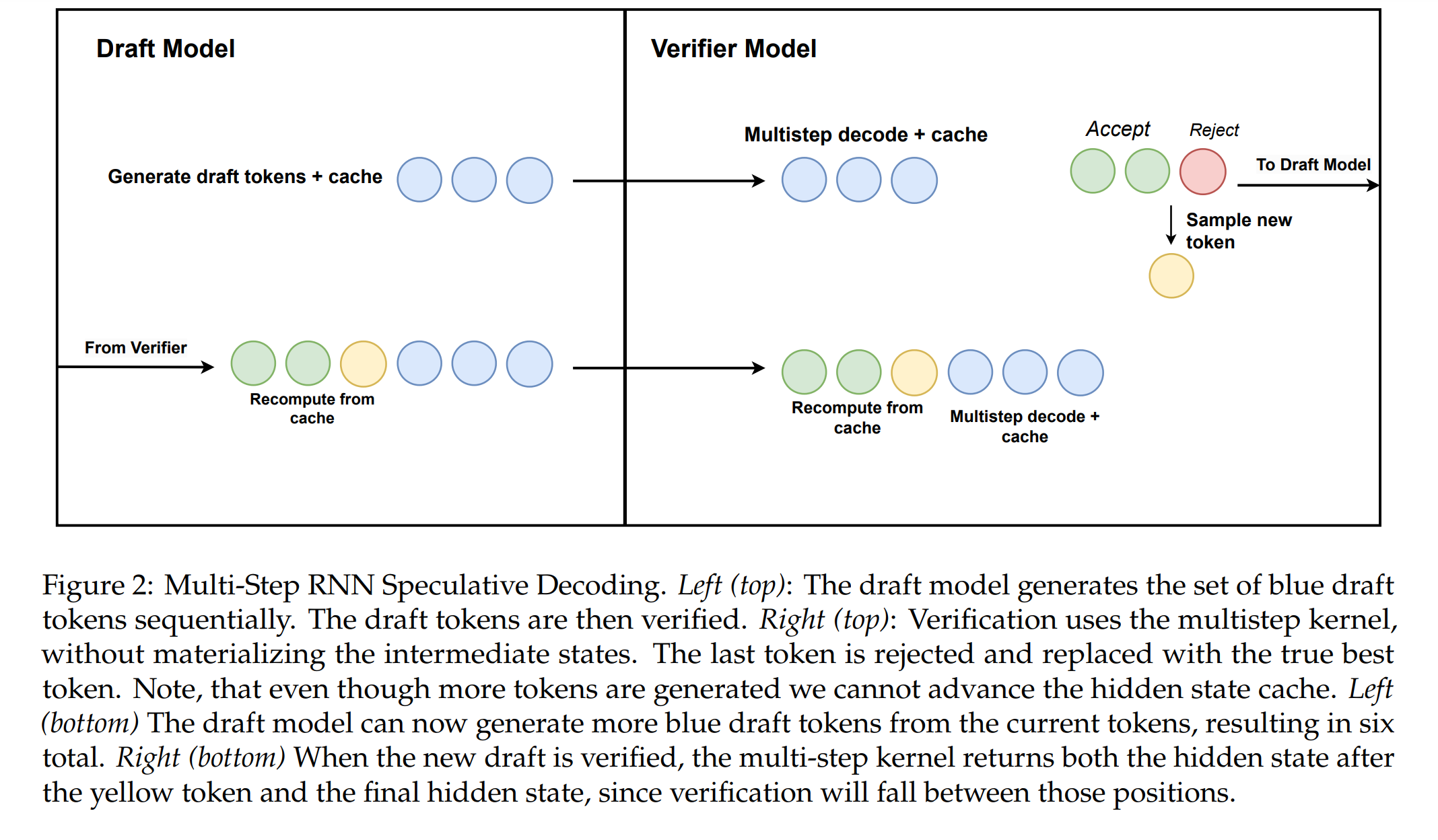
이 섹션에서는 선형 RNN 모델, 특히 Mamba 모델을 위한 추측적(예측적) 디코딩 알고리즘에 대해 설명합니다.

1. 추측적(예측적) 디코딩의 목적
   • 자기회귀적 생성의 직렬 의존성으로 인한 효율성 병목 현상 해결
   • 미래 생성에 대한 추측에 추가 계산을 사용하여 효율성 향상
2. RNN 추측의 챌린지
   • 드래프트 모델($\theta_D$)과 검증 모델($\theta_V$) 사용 → 최근 Speculative Diffusion Decoding과 비슷한 방법이지만 Diffusion 모델이 아닌 Mamba 아키텍처를 활용
   • RNN 모델의 상태 관리 및 되감기(rewinding) 문제
   • 하드웨어 인식 최적화의 필요성
3. 다단계 선형 RNN 추측 알고리즘
   • 핵심: 하드웨어 인식 다단계 생성 커널 사용 \(y_{j:k}, h_j, h_k \leftarrow \text{MultiStep}(h_i, y_{1:n}, i, j, k; A, B, C, \Delta)\)
   • 중간 상태를 구체화하지 않고 효율적인 계산 수행
   • 알고리즘 2와 Figure 2에서 전체 알고리즘 설명
4. 하이브리드 아키텍처에 대한 확장
   • RNN 층은 Algorithm 2에 따라 검증 수행
   • Transformer 층은 병렬 검증 수행
5. 성능 분석 및 하드웨어 특정 최적화
   • Table 1: 다양한 모델 크기와 GPU에 대한 속도 향상 결과
   • Figure 3: 다단계 SSM 커널의 성능 특성
   • H100 GPU에서의 최적화 챌린지 및 해결 방안

이런 알고리즘을 통해, 선형 RNN 기반 모델의 인퍼런스 속도를 크게 향상시킬 수 있으며, 특히 긴 시퀀스 생성 작업에서 효과적입니다. (mamba의 아키텍처의 가장 큰 특징)

1. 선형 RNN 모델의 특성에 맞춘 효율적인 추측적(예측적) 디코딩 구현
2. 하드웨어 인식 최적화를 통한 성능 향상
3. 하이브리드 아키텍처에 대한 적용 가능성

주요 수학적 기반

1. 추측적(예측적) 디코딩의 기본 개념 \(y^* = \arg\max_{y_{1:T}} p(y_1, ..., y_T; \theta_D)\) \(p(y^*_t \| y^*_{1:t-1}; \theta_V) \text{ Validation}\)

2. 다단계 커널의 수학적 표현 \(y_{j:k}, h_j, h_k \leftarrow \text{MultiStep}(h_i, y_{1:n}, i, j, k; A, B, C, \Delta)\)

3. 하드웨어 인식 최적화

   • 커널 융합
   • 캐싱 및 재계산 최적화

[참고 자료] Sepculative Decoding and Sampling

Speculative Decoding Algorithms이란?

주로 Draft Model(초기 시퀀스에 대한 드래프트 생성), Verifier or Decoding Model(수용/거부 결정, 메인 모델이 수행하는 것이 일반적), Main Model(LLM)으로 구성하여, 트랜스포머의 바닐라 어텐션의 선형적인 어텐션 스코어 계산량을 극복하기 위해 제시되고 있는 모델로, Speculative Sampling으로 인퍼런스 인퍼런스 속도의 한계를 극복하기 위해 제시되었으며, 현재 Mamba 혹은 Diffussion 아키텍처를 활용하는 연구가 진행 중인 알고리즘 (인퍼런스 시 토큰별로 매번 선형적으로 어텐션 스코어를 계산해야하는 병목을 개선하기 위해 제시되었음.)

1. Speculative Sampling의 기본 개념

Speculative sampling은 큰 언어 모델(메인 모델)의 인퍼런스 속도를 높이기 위해 작은 모델(드래프트 모델)을 사용하는 기법입니다. 이 방법의 핵심 아이디어는 다음과 같습니다.

드래프트 모델(Draft Model)을 사용하여 빠르게 토큰 시퀀스를 생성
→ 메인 모델을 사용하여 드래프트 모델이 생성한 토큰의 품질을 평가 (혹은 추가로 Decoding 혹은 Verifier를 구성하기도 함)
→ 품질이 좋은 토큰은 유지하고, 그렇지 않은 경우 메인 모델이 새로운 토큰을 생성합니다.

2. 단계별 과정 상세 설명

Step 1: 초기 입력 처리

• 입력 시퀀스 \(x = (x₁, x₂, \dots, xₙ)\)가 주어지며,

Step 2: 드래프트 모델의 토큰 생성

• 드래프트 모델 \(D\)는 입력 \(x\)를 바탕으로 \(K\)개의 토큰을 생성
• \[y' = (y'₁, y'₂, \dots, y'ₖ) = D(x)\]
• 이 과정은 빠르게 이루어집니다. (사용하는 주된 목적)

Step 3: 메인 모델의 확률 계산

• 메인 모델 \(M\)은 드래프트 모델이 생성한 각 토큰에 대해 확률을 계산
• \(P_M(y'ᵢ\|x, y'₁, \dots, y'ᵢ₋₁)\) for \(i = 1\) to \(K\)
• 이 단계에서 메인 모델은 각 토큰이 올바른지 평가

Step 4: 수용/거부 결정 (Decoding)

• 각 토큰 \(y'ᵢ\)에 대해
  • 수용 확률 계산: \(r = \min\left(1, \frac{P_M(y'ᵢ\\|x, y'₁, \dots, y'ᵢ₋₁)}{P_D(y'ᵢ\\\|x, y'₁, \dots, y'ᵢ₋₁)}\right)\)
  • 무작위 수 \(u\)를 \([0, 1]\) 범위에서 생성
  • 만약 \(u < r\)이면 토큰을 수용, 아니면 거부
• 첫 번째 거부된 토큰에서 과정을 중단

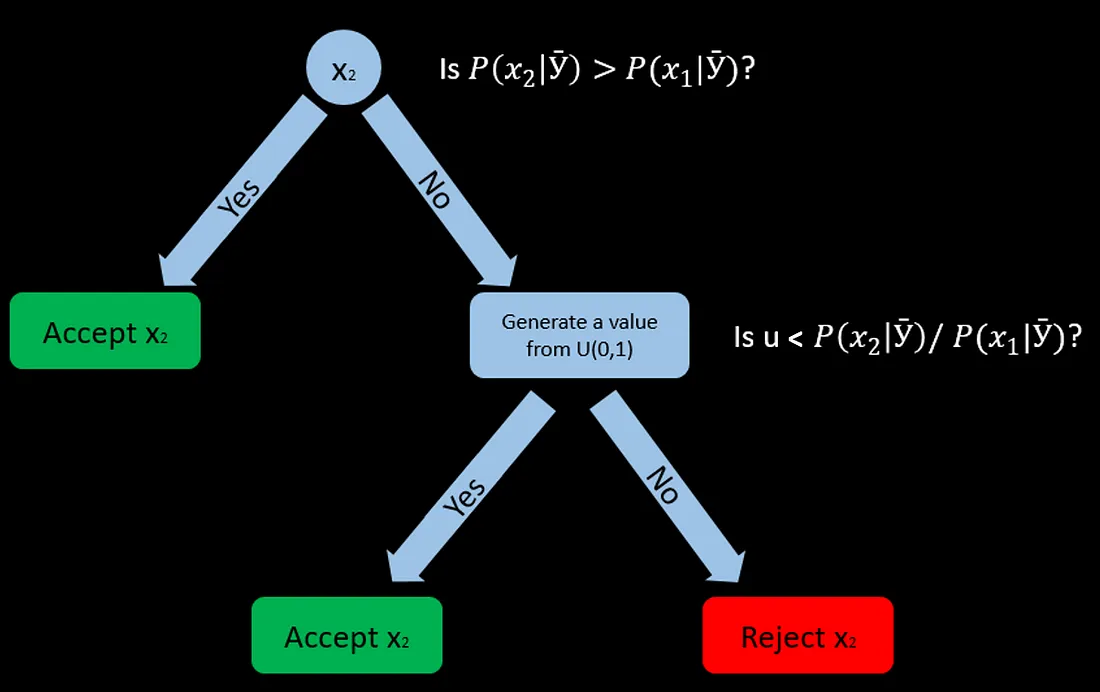*출처: An AR(1) model estimation with Metropolis Hastings algorithm

Step 5: 출력 생성 및 반복

• 수용된 토큰들을 출력에 추가
• 수용된 토큰들을 새로운 입력의 일부로 사용하여 과정을 반복

참고

• 드래프트 모델의 조건부 확률 \(P_D(y'ᵢ\|x, y'₁, \dots, y'ᵢ₋₁)\) = 드래프트 모델이 이전 토큰들이 주어졌을 때 \(y'ᵢ\)를 생성할 확률

• 메인 모델의 조건부 확률 \(P_M(y'ᵢ\|x, y'₁, \dots, y'ᵢ₋₁)\) = 메인 모델이 이전 토큰들이 주어졌을 때 \(y'ᵢ\)를 생성할 확률

• 수용 비율 (Acceptance ratio) \(r = \min\left(1, \frac{P_M(y'ᵢ\|x, y'₁, \dots, y'ᵢ₋₁)}{P_D(y'ᵢ\|x, y'₁, \dots, y'ᵢ₋₁)}\right)\)

이 수용 비율은 메트로폴리스-헤이스팅스 알고리즘(Metropolis-Hastings algorithm, MH Algorithm)에서 영감을 받았다고 하며, 비율이 1보다 크면 항상 수용하고, 1보다 작으면 그 확률로 수용하게 됩니다.

예시로 이해하기

입력: “The cat sat on”

드래프트 모델 출력 (\(K=4\))

메인 모델 확률 계산

드래프트 모델 확률 (가정)

수용 비율 계산

수용/거부 결정 (무작위 수 생성 가정)

\(u₁ = 0.3 < r₁\) → the 수용

\(u₂ = 0.8 < r₂\) → mat 수용

\(u₃ = 0.5 < r₃\) → and 수용

\(u₄ = 0.6 > r₄\) → slept 거부 및 중단

최종 출력: “The cat sat on the mat and”

코드로 이해하기

import numpy as np

class DraftModel:
    def __init__(self):
        self.vocab = ['the', 'mat', 'and', 'slept', 'cat', 'dog']
        self.probs = {
            'the': 0.7, 'mat': 0.5, 'and': 0.3, 'slept': 0.2, 'cat': 0.4, 'dog': 0.3
        }
    
    def generate(self, input_seq, k):
        return np.random.choice(self.vocab, k)
    
    def get_probability(self, token, context):
        return self.probs.get(token, 0.1)

class MainModel:
    def __init__(self):
        self.probs = {
            'the': 0.8, 'mat': 0.6, 'and': 0.2, 'slept': 0.1, 'cat': 0.5, 'dog': 0.4
        }
    
    def get_probability(self, token, context):
        return self.probs.get(token, 0.05)

def speculative_sampling(input_seq, draft_model, main_model, k):
    output = list(input_seq)
    
    while len(output) < len(input_seq) + 10:  # 10개 토큰 생성
        draft_tokens = draft_model.generate(output, k)
        
        for token in draft_tokens:
            p_main = main_model.get_probability(token, output)
            p_draft = draft_model.get_probability(token, output)
            
            acceptance_ratio = min(1, p_main / p_draft)
            
            if np.random.random() < acceptance_ratio:
                output.append(token)
                print(f"Accepted: {token} (ratio: {acceptance_ratio:.2f})")
            else:
                print(f"Rejected: {token} (ratio: {acceptance_ratio:.2f})")
                break
        
        if len(output) % k == 0:
            print(f"Current output: {' '.join(output)}")
    
    return ' '.join(output)

# 모델 및 입력 준비
draft_model = DraftModel()
main_model = MainModel()
input_seq = "The cat sat on".split()

# Speculative sampling 실행
result = speculative_sampling(input_seq, draft_model, main_model, k=4)
print("\nFinal output:", result)

1. 드래프트 모델과 메인 모델이 각각 고유한 확률 분포를 가지며,
2. 수용 비율을 계산하고 이를 기반으로 토큰을 수용 또는 거부합니다.
3. 과정의 각 단계를 출력하여 어떤 토큰이 수용되거나 거부되는지 확인할 수 있습니다.

4. 성능 및 한계

Speculative sampling의 주요 장점

• 작은 드래프트 모델을 사용하여 초기 예측을 빠르게 수행 (주 사용 목표)
• 메인 모델을 사용하여 최종 품질을 관리

한계점

• 두 개의 모델이 필요하므로 메모리 사용량이 증가 (매우 작은 Classifier 모델로 구성하기도 함.)
• 드래프트 모델의 성능이 너무 낮으면 대부분의 토큰이 거부되어 효율성이 떨어질 수 있음.
• 구현이 복잡하며(어떻게 쓸지에 따라 관리해야할 모델도 늘어날 수 있음. 단순하게 transformers에 Implementation된 코드를 사용할 경우 그렇게까지 번거롭지는 않으나 그러면 Specculative sampling을 사용하는 인퍼런스 속도를 손실된 성능만큼 제대로 trade-off로 가져오기 어려울 수 있음.), 특히 분산 환경에서 사용하기는 더 까다로울 수 있음.

실제 사용

OpenAI의 GPT-3, Google의 PaLM, Anthropic의 Claude 등 대규모 언어모델에서 활용되고 있으며, 특히 긴 텍스트 생성 작업에서는 성능의 큰 손실없이 상당한 속도 향상을 보여주고 있으므로 리소스 내에서 서빙하기 위해 필수적으로 사용되는 편입니다.

from transformers import AutoModelForCausalLM, AutoTokenizer
import torch

prompt = "What is Speculative Decoding and Sampling?"
checkpoint = "EleutherAI/pythia-1.4b-deduped"
assistant_checkpoint = "EleutherAI/pythia-160m-deduped"
device = "cuda" if torch.cuda.is_available() else "cpu"

tokenizer = AutoTokenizer.from_pretrained(checkpoint)
inputs = tokenizer(prompt, return_tensors="pt").to(device)

model = AutoModelForCausalLM.from_pretrained(checkpoint).to(device)
assistant_model = AutoModelForCausalLM.from_pretrained(assistant_checkpoint).to(device)
outputs = model.generate(**inputs, assistant_model=assistant_model)
print(tokenizer.batch_decode(outputs, skip_special_tokens=True))

두 개의 모델을 로드

• model: 메인 모델 (1.4B 파라미터)
• assistant_model: 드래프트 모델 (160M 파라미터)

Speculative decoding의 핵심 요소입니다. 작은 드래프트 모델(assistant_model)이 빠르게 초기 예측을 생성하고, 큰 메인 모델(model)이 이를 검증 (별도의 verifier 없이 main model verifier 혹은 토큰 수용/거부를 결정)

outputs = model.generate(**inputs, assistant_model=assistant_model)

generate 메소드에 assistant_model 파라미터를 전달함으로써 speculative decoding을 활성화합니다.

• 드래프트 모델(assistant_model)이 input을 받아 빠르게 여러 토큰을 생성
• 메인 모델(model)이 이 토큰들의 확률을 계산
• 메인 모델에 의해 각 토큰에 대해 수용/거부 결정이 이루어집니다. 수용된 토큰은 출력에 추가되고, 거부된 토큰에서 과정이 중단
• 이 과정이 반복되어 전체 시퀀스가 생성됩니다.

Hugging Face Transformers 라이브러리 내부에 구현되어 있어, 사용자는 단순히 assistant_model을 지정하는 것만으로 speculative decoding을 사용할 수 있습니다.

print(tokenizer.batch_decode(outputs, skip_special_tokens=True))

생성된 토큰 시퀀스를 다시 텍스트로 변환하여 출력

1. 이 구현에서는 드래프트 모델이 메인 모델보다 훨씬 작아 (160M vs 1.4B 파라미터) 빠르게 초기 인퍼런스 가능
2. Speculative decoding의 복잡한 로직(토큰 생성, 확률 계산, 수용/거부 결정)은 generate 메소드 내부에서 처리

특히 긴 시퀀스 생성 시 상당한 속도 향상

참고 논문

• Fast Inference from Transformers via Speculative Decoding
• DeepMind의 Accelerating Large Language Model Decoding with Speculative Sampling
• Google Fast Inference from Transformers via Speculative Decoding
• Google Blog
• Decoding Speculative Decoding

6. 분석

본 섹션에서는 Mamba 모델의 성능 개선을 위한 다양한 방법과 실험 결과를 분석합니다. 주요 내용으로는 증류 접근 방식의 비교, 정렬 방법의 영향, 그리고 다양한 모델 변형에 대한 절제 연구가 포함됩니다.

• Mamba 모델의 성능 개선을 위한 주요 방법 분석
• 다양한 초기화 및 구조 변경을 통한 Mamba 모델의 성능 향상
• 어텐션 메커니즘과 Mamba 블록의 조합을 통한 하이브리드 모델의 효과성 검증

Zephyr를 모델로 활용하고, OpenHermes 2.5 데이터셋을 SFT 데이터셋으로, UltraFeedback을 DPO 데이터셋으로 주로 활용

6.1 증류 접근 방식 비교

Table 6(왼쪽)에서는 다양한 모델 변형의 perplexity를 비교하고 있습니다. 이 실험에서는 Ultrachat를 시드 프롬프트로 사용하여 한 epoch 동안 증류를 수행했습니다. 실험 결과, 더 많은 레이어를 제거할수록 성능이 저하되는 것을 확인할 수 있습니다.

구체적으로, 어텐션 메커니즘의 비율에 따른 perplexity 변화는 다음과 같습니다.

Mamba 페이퍼의 rejection 이유 중 perplexity와 원래의 벤치마크로 검증하지 못 했으며, 특히 수학적인 백그라운드가 약했다는 지적에 따른 검증으로 보임.

1. 50% 어텐션 메커니즘: perplexity 비율 1.03
2. 25% 어텐션 메커니즘: perplexity 비율 1.09
3. 6.35% 어텐션 메커니즘: perplexity 비율 1.22
4. 어텐션 메커니즘 없음: perplexity 비율 3.36

이런 결과는 어텐션 메커니즘의 비율이 줄어들수록 모델의 성능이 점진적으로 저하됨을 보여줍니다. 특히, 어텐션 메커니즘을 완전히 제거했을 때 성능 저하가 가장 큰 것을 알 수 있습니다.

또한, 이 접근 방식을 [57]에서 제안된 이전 베이스라인과 비교하고 있습니다. 해당 베이스라인은 Transformer 모델을 Hyena 모델로 증류하는 방식을 사용했으며, 점진적 지식 전이 방법을 채택했습니다. 이 방법은 student 모델을 첫 번째 레이어부터 시작하여 점진적으로 후속 레이어로 확장하며 훈련시킵니다.

비록 직접적인 비교는 어렵지만, 본 논문의 증류 방법이 더 작은 성능 저하를 보이는 것으로 나타났습니다. DistillHyena 모델은 WikiText 데이터셋에서 훈련되었으며, 더 작은 모델을 사용했음에도 불구하고 더 큰 perplexity 저하를 보였습니다.

6.2 선호도 기반 증류의 효과

Table 6(오른쪽)에서는 증류 과정에서 다양한 정렬 단계의 영향을 보여줍니다. 실험 결과, 다음과 같은 중요한 발견을 할 수 있습니다.

1. SFT(Supervised Fine-Tuning) 또는 DPO(Direct Preference Optimization)만으로 큰 개선을 보이지는 않았으나,
2. SFT와 DPO를 결합했을 때, 가장 좋은 점수를 얻었습니다.

SFT 이후 DPO 혹은 PO는 이제 필수적으로…

이 실험에서는 Zephyr를 teacher 모델로 사용했으며, OpenHermes2.5 데이터셋을 SFT 데이터셋으로, UltraFeedback을 DPO 데이터셋으로 활용했습니다.

이런 결과는 선호도 기반의 학습이 단순한 지도 학습보다 더 효과적일 수 있음을 시사합니다. SFT와 DPO의 조합이 가장 좋은 성능을 보인 것은 두 방법이 상호 보완적으로 작용하여 모델의 전반적인 품질을 향상시킬 수 있다는 것을 의미합니다.

6.3 의사 레이블 증류 절제 연구

Table 7에서는 여러가지 모델 변형에 대한 절제 연구 결과를 보여줍니다. 이 실험들은 Ultrachat 데이터셋을 사용하여 5,000 스텝 동안 의사 레이블 접근 방식으로 훈련되었습니다.

Table 7(왼쪽)은 다양한 초기화 방법에 따른 증류 결과를 보여줍니다. 주요 발견은 다음과 같습니다.

1. Transformer로부터의 가중치 초기화가 성능에 중요한 역할을 합니다.
2. Transformer로부터의 가중치 초기화 없이는 순수 Mamba 모델과 하이브리드 모델 모두에서 perplexity가 크게 증가합니다.
3. MLP 레이어를 고정(freezing)하는 것이 student 모델이 토큰 간 상호작용을 학습하고 어텐션 레이어를 더 잘 모방하는 데 도움이 될 수 있습니다.

Table 7(오른쪽)에서는 점진적 증류와 Mamba 레이어와 어텐션 레이어의 교차 배치가 작은 이점을 제공한다는 것을 보여줍니다.

이런 결과는 모델 초기화와 구조가 증류 과정에서 중요한 역할을 한다는 것을 시사합니다. 특히, Transformer로부터의 가중치 초기화가 중요하며, MLP 레이어를 고정하는 것이 효과적일 수 있다는 점을 강조합니다.

6.4 어텐션 초기화의 영향

Table 8은 Mamba의 기본 랜덤 초기화와 어텐션 메커니즘으로부터 선형 투영을 재사용하는 방법을 비교합니다. 두 모델 모두 Zephyr를 teacher 모델로 사용하고, OpenHermes 2.5 데이터셋을 SFT 데이터셋으로, UltraFeedback을 DPO 데이터셋으로 사용하여 훈련되었습니다.

결과를 보면, 어텐션 메커니즘으로부터 선형 투영을 재사용하는 초기화 방법이 랜덤 초기화보다 모든 평가 벤치마크에서 더 좋은 성능을 보여 어텐션 가중치로부터의 초기화가 중요하다는 것을 반증한다고 언급합니다.

예를 들어, MMLU 벤치마크에서 어텐션 초기화를 사용한 모델은 55.01의 점수를 얻은 반면, 랜덤 초기화를 사용한 모델은 34.01의 점수를 얻어 어텐션 초기화가 모델의 일반적인 지식과 인퍼런스 능력을 크게 향상시킬 수 있음을 보여줍니다.

6.5 선형 RNN의 필요성

Table 9는 Mamba 블록을 완전히 제거한 모델과 Mamba 블록을 포함한 하이브리드 모델의 성능을 비교합니다. 두 모델 모두 동일한 방식으로 Zephyr를 teacher 모델로 사용하고, OpenHermes 2.5 데이터셋을 SFT 데이터셋으로, UltraFeedback을 DPO 데이터셋으로 사용하여 훈련되었습니다.

결과를 보면, Mamba 블록을 포함한 모델이 Mamba 블록을 제거한 모델보다 모든 평가 지표에서 좋은 성능을 보입니다. 예를 들어, LAMBADA 벤치마크에서 Mamba를 포함한 모델의 perplexity는 6.20인 반면, Mamba를 제거한 모델의 perplexity는 151.98로 크게 증가했습니다.

이런 결과는 Mamba 레이어를 추가하는 것이 중요하며, 향상된 성능이 단순히 남아있는 어텐션 메커니즘 때문만은 아니라는 것을 확인해줍니다. Mamba 블록이 모델의 전반적인 성능 향상에 크게 기여한다는 것을 알 수 있습니다.

결론적으로, 이 섹션의 실험 결과들은 Mamba 모델의 성능을 최적화하기 위해서는 어텐션 깊은 초기화 전략, Mamba 블록과 어텐션 메커니즘의 적절한 조합, 그리고 증류 과정에서의 다양한 기법들이 중요하다는 것을 보여줍니다.

7. 관련 연구

본 섹션에서는 Mamba 모델과 관련된 다양한 연구 분야를 살펴보고, 이들이 Mamba 모델의 발전에 어떤 영향을 미쳤는지 분석합니다.

• Mamba 모델의 한계와 관련 연구
• 어텐션 메커니즘 없는 모델들의 효율성과 성능 비교
• 트랜스포머 모델로부터의 지식 증류 및 추측 디코딩 기법의 발전

7.1 어텐션 메커니즘 없는 모델

어텐션 메커니즘 없는 모델들은 계산 및 메모리 효율성이 향상되어 자동회귀 언어 모델링을 포함한 다양한 언어 처리 작업에서 점점 더 인기를 얻고 있습니다. 이런 모델들의 주요 특징과 발전 과정은 다음과 같습니다.

1. S4 모델과 그 변형들
   • S4 [27]와 그 후속 변형 [26, 30]은 장거리 합성 작업 [66]에서 유망한 결과를 보여주었습니다.
   • 이 모델들은 어텐션 메커니즘 없이도 장거리 의존성을 효과적으로 처리할 수 있음을 입증했습니다.
2. 게이트된 SSM 아키텍처
   • GSS [49]와 BiGS [72]와 같은 모델들은 (양방향) 언어 모델링을 위해 SSM에 게이팅 메커니즘을 통합했습니다.
   • 이 접근 방식은 모델의 표현력을 향상시키면서도 계산 효율성을 유지하는 데 기여했습니다.
3. Mamba 모델
   • 최근 소개된 Mamba 모델 [25]은 이전 방법들의 SSM이 언어 모델링과 같은 작업에 중요할 수 있는 hidden state 내에서 입력 특정 컨텍스트 선택을 통합하지 못한다고 언급합니다.
   • 입니다.
   • Mamba는 다양한 모델 크기와 규모에서 Transformer를 능가하는 성능을 보여주었습니다.
4. 기타 서브 이차 모델 아키텍처:
   • [1, 2, 4, 18, 21, 55, 76]에서 제안된 여러 서브 이차 모델 아키텍처와 [22, 43]에서 제안된 하이브리드 아키텍처들도 주목할 만합니다.
   • 이런 모델들은 각각 고유한 방식으로 효율성과 성능의 균형을 추구하고 있습니다.

7.2 Transformer로부터의 증류

선형 RNN 스타일 모델로의 증류 시도는 상대적으로 적었습니다. 그러나 몇 가지 주목할 만한 연구가 있었습니다.

1. Laughing Hyena [48]
   • 긴 합성곱을 상태 공간 표현으로 증류하는 방법을 제안했습니다.
   • 이를 통해 Hyena [55]에서 상수 시간 인퍼런스이 가능해졌습니다.
2. Ralambomihanta et al. [57]의 연구
   • 작은 Transformer 모델(70M)을 Hyena 모델로 증류하기 위한 점진적 지식 접근 방식을 소개했습니다.
   • 이 방법은 모델 크기를 줄이면서도 성능을 유지하는 데 초점을 맞췄습니다.

7.3 추측 디코딩

추측 디코딩 [9, 10, 40, 64, 73]은 최근 대규모 언어모델, 특히 Transformer의 인퍼런스 과정을 가속화하기 위한 유망한 방법으로 부상했습니다. 이 접근 방식의 주요 특징은 다음과 같습니다.

1. 기본 개념
   • 더 작은 초안 모델을 사용하여 후보 토큰을 추측적으로 생성합니다.
   • 더 큰 대상 모델이 이를 검증합니다.
2. 주요 연구
   • Chen et al. [10]과 Leviathan et al. [40]은 인퍼런스 품질을 개선하기 위한 거부 샘플링 방식을 제안했습니다.
   • Spector and Re [64]는 더 효율적인 검증을 위해 후보 토큰을 트리 구조로 구성했습니다.
3. 후속 연구
   • 훈련된 초안 모델 [5, 12, 47]과 훈련 없는 초안 모델 [23, 31, 75] 모두에 대해 연구가 진행되었습니다.

7.4 한계점

본 연구의 잠재적 한계점은 주로 7B-9B 범위의 대규모 언어모델에 대해 평가가 수행되었다는 점입니다. 이로 인해 제안된 방법이 더 작은 규모의 모델에서도 동일하게 효과적일지는 불분명합니다. 이런 한계를 극복하기 위해 다음과 같은 후속 연구가 필요하다고 언급합니다. (아무래도 리소스의 한계로 인해, Jamba처럼 AI21labs와 같은 기업 단위의 추가 검증이 필요할 것 같습니다.)

1. 소규모 모델에 대한 적용
   • 계산적으로 더 효율적인 소규모 모델에 대한 본 접근 방식의 적용 가능성을 탐구해야 합니다.
2. 추가 실험 필요
   • 더 작은 Transformer 모델을 처음부터 훈련하고 증류 기법을 적용하는 실험을 수행해야 합니다.
   • 다양한 메트릭에 걸쳐 이들의 성능을 평가해야 합니다.