Scaling Law | Transfer Scaling Law***

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-27

Empirical Study of Scaling Laws for Transfer

• url: https://arxiv.org/abs/2408.16947
• pdf: https://arxiv.org/pdf/2408.16947
• html: https://arxiv.org/html/2408.16947v1
• abstract: We present a limited empirical study of scaling laws for transfer learning in transformer models. More specifically, we examine a scaling law that incorporates a “transfer gap” term, indicating the effectiveness of pre-training on one distribution when optimizing for downstream performance on another distribution. When the transfer gap is low, pre-training is a cost-effective strategy for improving downstream performance. Conversely, when the gap is high, collecting high-quality fine-tuning data becomes relatively more cost effective. Fitting the scaling law to experiments from diverse datasets reveals significant variations in the transfer gap across distributions. In theory, the scaling law can inform optimal data allocation strategies and highlights how the scarcity of downstream data can bottleneck performance. Our findings contribute to a principled way to measure transfer learning efficiency and understand how data availability affects capabilities.

TL;DR

1. 이 연구는 전이 학습(transfer learning)의 스케일링 법칙을 탐구하여 pre-training dataset와 파인튜닝 데이터 간의 관계를 분석합니다.
2. 연구진은 사전 학습 단계와 파인튜닝 데이터 크기에 따른 성능 변화를 모델링하는 새로운 스케일링 법칙 공식을 제안합니다.
3. 이 스케일링 법칙을 통해 ‘전이 격차(transfer gap)’라는 개념을 도입하여 다양한 작업 간의 지식 전이 효율성을 정량화합니다.

1. 서론

최근 몇 년간 머신러닝 분야에서는 스케일링 법칙(scaling laws)에 대한 연구가 활발히 진행되어 왔습니다. 스케일링 법칙이란 모델의 성능이 파라미터 수와 데이터 크기 등의 요인에 따라 어떻게 변화하는지를 설명하는 경험적 규칙성을 말합니다.

특히 Hernandez 등(2021)의 연구는 전이 학습의 스케일링 법칙을 다루었는데, 이들은 모델 크기와 파인튜닝 데이터 크기에 따른 전이 학습의 특성 변화를 분석했습니다. 주요 발견은 전이의 정도(degree of transfer)가 파라미터 수와 파인튜닝 데이터 크기에 대해 단순한 멱법칙(power law)을 따른다는 것이었습니다.

전이 학습의 스케일링 법칙은 특정 작업에 대한 머신러닝의 진전이 데이터에 의해 얼마나 제한되는지를 알려주기 때문에 중요합니다. 예를 들어, 파운데이션 모델(foundation model) 패러다임에서는 대규모의 다양한 분포에 대해 사전 학습된 모델을 특정 하위 작업에 대해 파인튜닝하는 방식이 일반적입니다. 이런 접근 방식의 효과는 사전 학습된 모델로부터 하위 작업 또는 분포로의 지식 전이 정도에 크게 의존합니다.

두 분포 간의 전이 격차(transfer gap)를 측정하기 위한 간단한 프레임워크를 고안했습니다. 전이 격차란 사전 학습의 최대 이론적 이점을 의미하며, 이는 무한한 pre-training dataset의 극한에서 달성 가능한 값입니다. 구체적으로, 전이 격차는 사전 학습 변수가 무한대로 접근할 때 전이 스케일링 법칙의 극한값을 평가함으로써 얻어지는 양입니다.

다양한 함수 형태의 예측 타당성을 경험적으로 비교한 결과, 다음과 같은 전이 스케일링 법칙을 제안합니다. $p$는 사전 학습 단계의 수를, $f$는 파인튜닝 데이터 포인트의 수를 나타냅니다.

이 스케일링 법칙에서 전이 격차 $G$는 무한한 pre-training dataset의 극한에서 파인튜닝의 효율성을 결정합니다. 비용이 저렴하고 풍부한 사전 학습 분포에서 비용이 많이 드는 하위 분포로의 전이 격차를 측정함으로써, 특정 하위 분포에 대한 사전 학습의 잠재적 성능 향상을 예측할 수 있습니다.

연구는 Pythia 모델 제품군을 크게 활용하여, 다양한 모델 크기와 학습 체크포인트에서의 트랜스포머 모델들을 제공합니다. 28억 파라미터 모델을 수학, 유전자 서열, 통계학 교과서, 가상의 전기 등 다양한 하위 언어 데이터셋에 대해 파인튜닝했습니다. 스케일링 법칙을 경험적 데이터에 맞춘 후, 이 법칙을 사용하여 “특정 작업에 대해 파인튜닝 데이터를 더 수집하는 것이 pre-training dataset를 확장하는 것에 비해 얼마나 가치가 있는가?” 또는 “한 분포에서 다른 분포로의 전이 격차는 얼마인가?”와 같은 구체적인 질문들에 답할 수 있음을 보여줍니다.

2. 관련 연구

신경망 스케일링 법칙에 대한 현대적 연구는 Hestness 등(2017)의 연구로부터 시작되었습니다. 그들은 이미지, 언어, 음성 도메인에서 데이터 크기와 오류 간의 멱법칙 관계를 관찰했습니다. 유사하게, Rosenfeld 등(2019)은 모델 크기와 데이터 모두와 관련된 멱법칙 관계를 식별했습니다. Kaplan 등(2020)과 Hoffmann 등(2022)의 연구는 언어 모델링에서 이 연구를 더욱 발전시켰으며, 컴퓨팅 예산 할당에 대한 함의를 강조했습니다.

Hernandez 등(2021)은 모델 크기와 파인튜닝 데이터에 대한 전이 스케일링 법칙을 연구했습니다. 본 연구는 선행 연구와 세 가지 차이가 있습니다.

1. 사전 학습 단계와 파인튜닝 데이터를 조사합니다.
2. 전이된 유효 데이터를 연구하는 대신, 학습 입력의 함수로 테스트 손실이 어떻게 변하는지를 직접 조사합니다.
3. 영어에서 Python으로의 전이뿐만 아니라 다양한 데이터셋 간의 전이를 조사합니다.

Mikami 등(2021)의 연구도 접근 방식과 유사하게 pre-training dataset가 전이 특성에 미치는 영향을 조사했습니다. 그러나 연구는 pre-training dataset가 아닌 파인튜닝 데이터에 대해 모델을 수렴까지 학습시켰다는 점에서 차이가 있습니다. 또한, 다양한 분포 간의 ‘전이 격차’를 더 직접적으로 측정하고자 했으며, 이런 격차가 대규모 머신러닝 모델 학습 시 경제적 트레이드오프에 어떤 정보를 제공하는지를 보여주고자 했습니다.

3. 전이를 위한 스케일링 법칙

Pythia 모델 제품군의 28억 파라미터 트랜스포머 모델을 사용하여 전이 학습의 스케일링 법칙을 조사했습니다. 구체적으로, 사전 학습 토큰 수 $p$와 파인튜닝 데이터 크기 $f$에 따른 파인튜닝 분포의 교차 엔트로피 손실을 관련짓는 경험적 데이터에 스케일링 법칙을 맞추고자 했습니다.

여러 잠재적 스케일링 법칙 형태를 고려한 결과, 간단하면서도 경험적 테스트에 따라 잘 수행되는 것으로 보이는 형태를 식별했습니다. 이 형태는 Mikami 등(2021)의 연구에서 직접 가져온 것이며, 제시된 분석의 기초가 됩니다.

이 스케일링 법칙은 네 가지 distinct한 항으로 구성됩니다.

1. 사전 학습 항 $A \cdot p^{-\alpha}$: pre-training dataset 단계에 대한 멱법칙입니다.
2. 전이 격차 $G$: 무한한 사전 학습 체제에서 사전 학습 분포에서 파인튜닝 분포로의 전이 학습의 궁극적 효율성을 설정합니다.
3. 파인튜닝 항 $f^{-\beta}$: 파인튜닝 데이터에 대한 멱법칙입니다.
4. 본질적 엔트로피 $E$: 파인튜닝 분포의 본질적 엔트로피로, 학습 성능의 이론적 최대 한계를 설정합니다.

전이 격차의 유용성은 \(\lim_{p \to \infty} L(p,f)\)를 고려함으로써 알 수 있다고 주장하며, 무한한 사전 학습 체제에서 괄호 안에 남는 유일한 값은 전이 격차 $G$입니다. 이는 사전 학습 분포에서 파인튜닝 분포로의 전이 학습의 궁극적 효율성을 암묵적으로 설정합니다.

이 스케일링 법칙을 Hernandez 등(2021)이 제안한 스케일링 법칙과 비교하고, 이것이 어떻게 도출될 수 있는지를 Appendix A에서 논의합니다. 그러나 고려하지 않은 많은 잠재적 형태가 있을 수 있음을 주목해야 합니다. 따라서 다른 함수 형태가 데이터를 더 잘 예측할 가능성이 높습니다.

여러 스케일링 법칙 형태를 서로 비교하기 위해, 4.3절에서 설명하는 교차 검증 형태를 사용하여 모델이 분포 외 데이터를 얼마나 잘 예측하는지 테스트합니다. 또한 부트스트래핑을 사용하여 적합도 통계를 계산합니다.

이런 방법을 통해 전이 학습의 특성을 더 정확히 이해하고, 다양한 작업 간의 지식 전이 효율성을 정량화할 수 있어 학습 전략을 수립할 때 도움이 될 수 있다고 언급합니다.

4. 방법

4.1 데이터셋

트랜스포머 모델의 전이 학습 특성을 경험적으로 측정하기 위해, 5개의 데이터셋을 사용하여 모델을 파인튜닝했습니다. 4개의 다양한 언어 데이터셋과 1개의 생물학적 시퀀스 데이터셋입니다.

1. Fictional encyclopedia: GPT-3.5로 생성된 가상 우주의 전기를 시뮬레이션한 합성 데이터셋
2. Math arXiv: 최근의 수학 논문들로 구성된 LaTeX 형식의 데이터셋
3. Statistics textbook: “Statistics for Ecologists” 교과서에서 파생된 데이터셋
4. Enron emails: 실제 기업 이메일 통신 데이터를 포함하는 Enron 이메일 데이터셋의 부분집합
5. House cat genome: 가정 고양이의 시퀀싱된 게놈으로 구성된 생물학 및 유전학 연구용 데이터셋

이 다양한 데이터셋을 선택한 이유는 다음과 같습니다. 1) 합성 데이터셋을 통해 새로운 분포에 대한 진정한 전이를 발견할 수 있는지 테스트 2) pre-training dataset에 포함되지 않은 데이터셋(Math arXiv, Statistics textbook)을 사용하여 새로운 지식에 대한 전이 학습 능력 평가 3) pre-training dataset에 포함된 데이터셋(Enron emails)을 사용하여 이미 학습된 정보에 대한 전이 학습 특성 분석 4) 다른 분포(House cat genome)에 대한 전이 학습 격차 측정

4.2 학습

Pythia 모델 제품군의 28억 파라미터 트랜스포머 모델을 사용했습니다. 이 모델은 The Pile 데이터셋으로 사전 학습되었습니다. 구체적으로:

1. 15개의 체크포인트를 선택 (최종 체크포인트: 143,000 단계, 배치 크기 2,097,152 토큰)
2. 각 체크포인트와 데이터셋에 대해 15개의 실험 수행
3. 데이터셋의 부분집합(10-1,100 토큰)으로 모델을 수렴할 때까지 파인튜닝
4. 컨텍스트 길이 256, 전체 파라미터 파인튜닝 방식 사용

학습 세부 사항

• H100 GPU 사용
• 배치 크기: 10
• 그래디언트 누적 단계: 25
• 옵티마이저: AdamW (학습률 $1 \times 10^{-5}$, 베타 0.9 및 0.999, 엡실론 $1 \times 10^{-8}$, 가중치 감쇠 없음)
• 조기 종료 인내심: 3

총 750번의 학습 실행을 수행했습니다.

4.3 스케일링 법칙 평가

스케일링 법칙의 견고성을 이해하기 위해, 데이터에 대해 다음과 같은 단계별 교차 검증을 수행했습니다.

1. 각 입력 변수(사전 학습 토큰 수, 파인튜닝 데이터 크기)에 대한 임계값 설정
2. 모든 가능한 임계값 조합 생성
3. 각 조합에 대해
   • 임계값 이하의 데이터 포인트로 훈련 세트 구성
   • 임계값 초과의 데이터 포인트로 테스트 세트 구성
   • 훈련 세트로 스케일링 법칙 적합
   • 테스트 세트로 평가

이 과정을 통해 모델의 일반화 능력과 더 많은 사전 학습 단계나 파인튜닝 데이터 포인트로 학습된 언어 모델에 대한 정확한 예측 능력을 평가할 수 있었다고 합니다. 추가로, 각 일반 스케일링 법칙에 대해 L2 정규화를 적용했으며, 각 스케일링 법칙 변형에 대해 다양한 하이퍼파라미터 선택을 사용했다고 합니다.

5. 결과

5.1 사전 학습과 전이 학습

사전 학습은 전이 격차와 상대적으로 독립적으로 손실을 감소시킨다.

적합한 주요 방정식은 다음과 같습니다.

데이터셋 간 파라미터 값을 비교한 결과

1. 사전 학습 항의 지수 $\alpha$는 다른 항들에 비해 상대적으로 낮은 변동을 보였으며,
2. $\alpha$의 변동 계수는 파인튜닝 지수 $\beta$의 변동 계수의 25% 미만이었습니다.

이는 사전 학습이 전이 격차 $G$와 독립적으로 일관된 손실 감소 기여를 한다는 것을 시사합니다. 이는 전이 격차를 두 분포 간의 유향 근접성(directed proximity)을 나타내는 것으로 해석하는 데 힘을 실어줍니다.

흥미롭게도, 고양이 게놈 데이터셋의 전이 격차는 상대적으로 작았습니다(0.548). 이는 직관과 달리 보이지만, 이 데이터셋의 높은 추정 본질적 손실(2.677)을 고려하면 이해할 수 있습니다. 이는 데이터셋이 높은 본질적 엔트로피를 가지고 있고 상대적으로 학습 가능한 구조가 적다는 것을 나타냅니다.

5.2 전이를 위한 스케일링 법칙

전이를 위한 스케일링 법칙은 상대적으로 적은 계산으로도 효율적으로 추정될 수 있다고 언급합니다.

데이터셋당 150개의 데이터 포인트만을 사용했음에도 불구하고, 각 데이터셋에 대해 상당히 견고한 스케일링 법칙 적합을 얻었습니다.

1. 지수 파라미터의 표준 오차는 일반적으로 0.01에서 0.03 사이였으며,
2. 이는 Hoffmann 등(2022)의 연구에서의 표준 오차(약 0.02)와 유사한 수준의 불확실성을 나타냅니다.

실험에 필요한 계산량을 추정하기 위해, 다음 휴리스틱을 사용했습니다.

$N$은 모델의 파라미터 수, $D$는 한 에포크 동안 본 토큰의 수

총 750번의 학습 실행에 대해, 다음 공식을 사용했습니다.

이 공식을 사용하여 얻은 총 추정 계산량은 약 $4.77 \times 10^{16}$ FLOP으로, Meta의 Llama 3 70B 모델 훈련에 사용된 추정 계산량의 백만분의 1 미만입니다.

6. 논의

6.1 사전 학습과 파인튜닝 데이터 수집 간의 트레이드오프

파인튜닝 데이터 수집에 비용이 들고 고정된 예산이 있는 상황을 고려해보면, 사전 학습 확장 또는 더 많은 파인튜닝 데이터 수집에 예산을 사용할 수 있습니다. 전이를 위한 스케일링 법칙을 활용하여 어떤 상황에서 더 많은 데이터를 수집하거나 사전 학습을 확장하는 것이 가치 있는지에 대한 결정을 내릴 수 있다고 언급합니다.

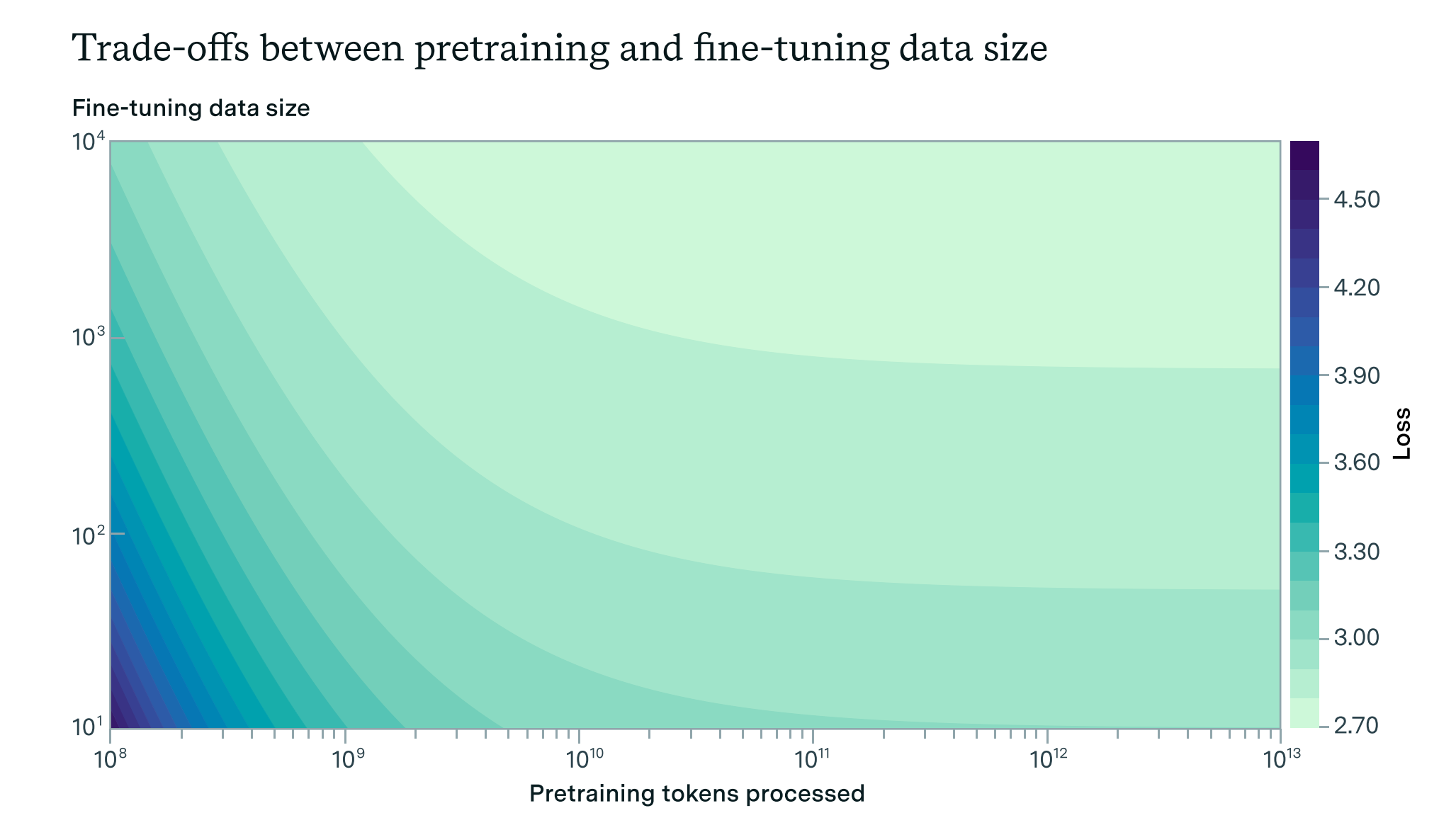
Figure 1: This plot presents the trade-offs between expanding pre-training and collecting more fine-tuning data to achieve low loss on the synthetic fictional encyclopedia dataset. The isolines, or lines of equivalent loss values, delineate the points at which equal loss is achievable given different combinations of pre-training steps and finetuning data points. The plot demonstrates that at low pre-training values, significant benefits can be gained from both increasing fine-tuning data and expanding pre-training. Conversely, at high pre-training values, the marginal benefit of additional pre-training diminishes, making the collection of more fine-tuning data points increasingly valuable for reducing loss.

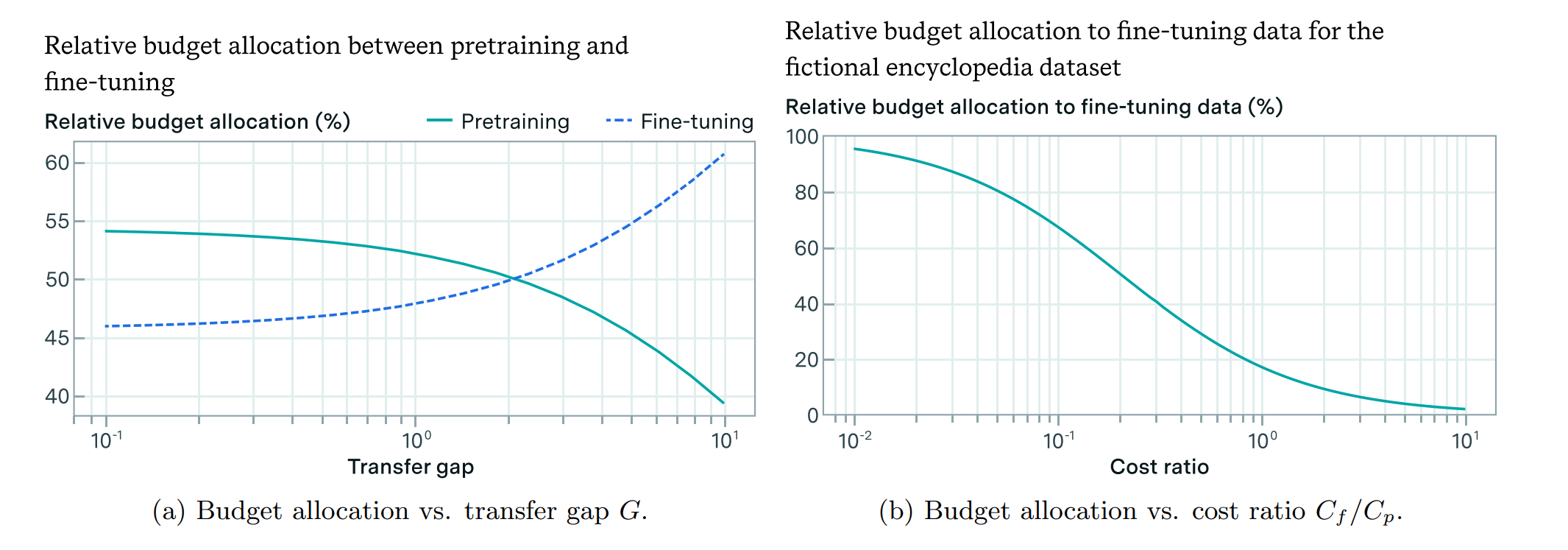
최적화 문제

$B$는 예산, $C_p$는 단일 사전 학습 단계의 비용, $C_f$는 파인튜닝 데이터 포인트 수집 및 학습 비용

1. 전이 격차 $G$가 낮을 때: 예산을 주로 사전 학습 확장에 할당하는 것이 비용 효율적
2. 전이 격차 $G$가 높을 때: 예산을 주로 파인튜닝 데이터 수집에 할당하는 것이 유리

이는 분포 간 전이가 낮을 때 사전 학습이 더 비용 효율적임을 나타내며, 학습 리소스 할당 시 전이 격차를 이해하는 것의 전략적 중요성을 강조합니다.

6.2 새로운 도메인에서의 전이 격차

전이 격차는 새로운 도메인에서 높은 성능 달성의 난이도를 설정할 수 있다고 언급합니다.

작업의 본질적 복잡성이 모델 훈련의 주요 난이도를 결정하는 것으로 보이지만, 자연어 처리 분야는 이에 대한 반례를 제시합니다. 자연어의 방대한 복잡성에도 불구하고, 대규모 언어모델의 개발과 적용을 통해 번역 및 분류와 같은 전통적인 NLP 작업의 자동화에 상당한 진전이 있었습니다.

이런 진전이 주로 인터넷에서 자유롭게 사용할 수 있는 방대한 양의 자연어 데이터 덕분이라고 생각합니다. 이는 전례 없는 규모로 이런 모델을 훈련할 수 있게 했습니다. NLP 작업 자동화의 성공은 풍부하고 관련성 있는 훈련 데이터의 가용성이 본질적으로 복잡한 작업의 챌린지를 극복하는 데 도움이 될 수 있음을 시사합니다.

로봇공학과 같이 데이터가 덜 풍부한 도메인에서는, 저렴하고 풍부한 사전 학습 분포에서 관심 있는 하위 작업으로의 전이 격차가 이런 도메인에서 높은 성능을 달성하는 난이도에 상당한 영향을 미칠 수 있다고 추측합니다.

프레임워크는 전이 격차를 직접 측정할 수 있게 해주므로, 다양한 도메인의 작업에서 높은 성능을 달성하는 난이도를 추정하는 데 유용한 도구가 될 수 있습니다. 저렴하고 풍부한 pre-training dataset(e.g., 인터넷 텍스트 데이터)와 목표 작업 데이터 간의 전이 격차를 정량화함으로 성능 향상을 위한 방법들을 탐구합니다.

Appendix

Appendix A: 전이 학습을 위한 스케일링 법칙에 대한 상세 설명

이 Appendix에서는 전이 학습(Transfer Learning)에 대한 스케일링 법칙을 어떻게 도출했는지 상세히 설명합니다. 이 연구의 목적은 사전 학습(pre-training)과 파인튜닝(fine-tuning)이 모델 성능에 미치는 영향을 수학적으로 정량화하는 것입니다.

스케일링 법칙의 기본 개념

연구자들은 Mikami et al. (2021)의 연구를 기반으로 하되, 자연어 처리 태스크에 맞게 수정했습니다. 주요 차이점은 다음과 같습니다.

1. 이미지의 L2 손실 대신 자연어의 교차 엔트로피 손실을 사용
2. 파인튜닝 데이터 포인트 수 대신 파인튜닝 데이터 크기를 변수로 사용

스케일링 법칙의 네 가지 조건

연구자들은 스케일링 법칙이 만족해야 할 네 가지 조건을 제시했습니다.

1. 불가역 오차 (Irreducible error)

   $\lim_{f \to \infty} L(p,f) = E$

   이는 파인튜닝 데이터를 무한히 늘려도 도달할 수 없는 최소 오차를 의미합니다.

2. 최대 사전 학습에서의 멱법칙 (Power law with maximum pre-training)

   $\lim_{p \to \infty} L(p,f) = G \cdot f^{-\beta} + E$

   pre-training dataset를 무한히 늘렸을 때, 파인튜닝 데이터에 대한 멱법칙 관계를 나타냅니다.

3. 사전 학습 없는 멱법칙 (Power law with no pre-training)

   $L(0,f) = C \cdot f^{-\beta} + E$

   사전 학습 없이 파인튜닝만 했을 때의 성능을 나타냅니다.

4. 파인튜닝 없는 멱법칙과 전이 갭 (Power law plus transfer gap with no fine-tuning)

   $L(p,0) = A \cdot p^{-\alpha} + G + E$

   파인튜닝 없이 사전 학습만 했을 때의 성능을 나타냅니다. ($L(p,f)$는 손실 함수, $p$는 pre-training dataset 양, $f$는 파인튜닝 데이터 양)

제안된 스케일링 법칙의 형태

위 조건들을 만족하는 스케일링 법칙의 형태로 다음을 제안했습니다.

$L(p,f) = (G + A \cdot p^{-\alpha}) \cdot f^{-\beta} + E$

• $A \cdot p^{-\alpha} \cdot f^{-\beta}$: 사전 학습과 파인튜닝의 상호작용 효과
• $G \cdot f^{-\beta}$: 파인튜닝만의 효과
• $E$: 불가역 오차

실제 적용을 위한 수정

실제 데이터에 적용할 때는 $p$와 $f$를 각각 $p-1$과 $f-1$로 수정했습니다.

$L(p,f) = (A \cdot (p+1)^{-\alpha} + G) \cdot (f+1)^{-\beta} + E$

$p=0$ 또는 $f=0$일 때 수학적으로 정의되지 않는 문제를 해결하고, 조건 3과 4를 정확히 만족시키기 위해 위와 같이 수정합니다.

경험적 검증

연구자들은 다양한 형태의 스케일링 법칙을 탐색하고 광범위한 교차 검증을 통해 이 형태의 우수성을 확인했습니다. 이 과정은 Appendix D에서 자세히 설명됩니다.

다른 연구와의 비교

Hernandez et al. (2021)의 연구에서는 ‘효과적으로 전이된 데이터’(effective data transferred)라는 개념을 사용했습니다. 반면, 이 연구에서는 pre-training dataset와 파인튜닝 데이터의 직접적인 함수로 손실을 표현했습니다. 이 접근 방식은 더 직관적이고 해석하기 쉬운 장점이 있습니다.

이 연구에서 제안한 스케일링 법칙은 다음과 같은 의의를 갖습니다.

1. 사전 학습과 파인튜닝의 상호작용을 표현하고,
2. 다양한 데이터셋에 대해 전이 학습의 효과를 정량적으로 분석할 수 있게 해줍니다.
3. 모델 학습 전략을 수립할 때 사전 학습과 파인튜닝에 얼마나 자원을 할당할지 결정하는 데 도움을 줄 수 있습니다.

Appendix B: 실험 데이터의 분석 및 제시

이 Appendix에서는 실험 결과에 대한 심층적인 분석을 제공합니다. 연구자들은 다양한 사전 학습 단계와 파인튜닝 데이터 크기에 따른 모델 성능을 분석하여 전이 학습의 효과를 명확히 보여주고 있습니다.

주요 발견

1. 전이 학습의 상대적으로 명확한 증거
   • 대부분의 데이터셋에서 pre-training dataset가 증가함에 따라 손실이 부드럽게 감소하는 패턴을 보임
   • 예외: 고양이 게놈 데이터셋은 다른 데이터셋과 달리 불규칙한 패턴을 보임 (pre-training dataset와의 유사성이 낮기 때문으로 추정)
2. 스케일링 법칙의 적합성
   • Figure 4는 가상 백과사전 데이터셋에 대한 스케일링 법칙의 적합도를 3D 그래프로 보여줌
   • 사전 학습 단계와 파인튜닝 데이터 포인트 모두에서 멱법칙과 유사한 관계가 잘 포착됨
   • 단순한 형태의 스케일링 법칙임에도 과적합의 징후 없이 데이터를 잘 모델링함
3. 데이터셋별 최적 전략의 차이
   • Figure 6의 등손실 곡선은 각 데이터셋에 대한 최적의 학습 전략이 다름을 보여줌
     • (e.g., 수학 arXiv 데이터셋은 높은 수준의 사전 학습에서도 사전 학습이 효과적)
   • 대조적으로, 가상 백과사전 데이터셋은 낮은 사전 학습 영역에서만 사전 학습이 유익함

방법 및 데이터 분석

1. 실험 설계
   • 2.8억 파라미터의 Pythia 모델 사용
   • 다양한 사전 학습 체크포인트에서 파인튜닝 수행
   • 각 파인튜닝 데이터셋에 대해 150개의 실험 수행 (총 750개 실험)
2. 스케일링 법칙 피팅 방법
   • BFGS 최적화 방법 사용
   • Huber 손실 함수 사용 (δ = 10^-3)
   • 초기 추정치 그리드 사용
3. 교차 검증
   • 단계별 교차 검증 방법 사용
   • 다양한 데이터 임계값과 정규화 값 조합 사용
   • L2 정규화를 지수와 계수에 적용
4. 수렴까지의 에포크 수 분석
   • 사전 학습이 많을수록 일반적으로 더 적은 에포크에서 수렴
   • 파인튜닝 데이터 크기에 대해서는 명확한 경향성이 없음

이 Appendix의 분석은 제안된 스케일링 법칙이 다양한 데이터셋에 대해 전이 학습의 효과를 잘 포착하고 있음을 보입니다. 또한, 각 데이터셋의 특성에 따라 최적의 학습 전략이 다를 수 있음을 시사하며, 이는 모델 학습 시 자원 할당 전략 수립에 중요한 지침을 제공합니다.

Appendix C: 실험 방법에 대한 추가 정보

이 Appendix에서는 연구에 사용된 실험 방법에 대한 자세한 정보를 제공합니다. 연구자들은 다양한 사전 학습 단계와 파인튜닝 데이터 크기를 조합하여 광범위한 실험을 수행했습니다.

실험 설계

1. 모델: 2.8억 파라미터의 Pythia 모델 사용
2. 데이터셋: 5개의 파인튜닝 데이터셋 사용 (Table 1 참조)
3. 실험 구성:
   • 사전 학습 토큰 수: 5.37×10^8부터 2.99×10^11까지 15단계
   • 파인튜닝 데이터 크기: 10 토큰부터 2.99×10^11 토큰까지 10단계
   • 각 데이터셋당 150개 실험, 총 750개 실험 수행
4. 측정 지표:
   • 최종 최소 평가 손실값
   • 사전 학습에서 본 토큰 수
   • 파인튜닝 데이터 크기
   • 수렴까지의 에포크 수

스케일링 법칙 피팅 방법

연구자들은 BFGS 최적화 방법을 사용하여 스케일링 법칙의 파라미터를 찾았습니다. 최적화 문제는 다음과 같이 정의됩니다.

• $A = \exp(a)$, $G = \exp(g)$, $E = \exp(e)$
• $f_i$: 파인튜닝 데이터 크기
• $p_i$: 사전 학습 토큰 수
• $L_i$: 실제 손실값

최적화 과정

1. 추정치 그리드 초기화
2. Huber 손실 함수 사용 (δ = 10^-3)
3. 반복적으로 추정치 개선

교차 검증 방법

연구자들은 ‘단계별 교차 검증’이라는 새로운 방법을 제안하며, 이 방법의 주요 특징은 다음과 같습니다.

1. 데이터 분할: 다양한 임계값 조합을 사용하여 훈련 및 테스트 세트 생성
2. 모델 훈련 및 평가: basinhopping 최적화 기법 사용
3. L2 정규화: 지수와 계수에 대해 별도의 정규화 적용
4. 성능 평가: RMSE와 MAE 사용

이 방법은 다양한 시나리오에서 모델의 성능을 철저히 조사할 수 있게 해주며, 스케일링 법칙 함수의 파라미터 선택에 대한 신뢰성을 높일 수 있다고 언급합니다.

이 Appendix에서 설명한 실험 방법은 연구의 신뢰성과 재현 가능성을 높이는 데 기여하고 특히, 광범위한 실험 설계와 엄격한 교차 검증 방법은 제안된 스케일링 법칙의 견고성을 보장하기 위해 도움을 줄 수 있습니다. 이런 방법은 향후 유사한 연구에서 참고할 수 있는 기준을 제시합니다.

Appendix D: 스케일링 법칙 형태의 비교

이 Appendix에서는 연구자들이 제안한 다양한 스케일링 법칙 형태를 비교하고 평가하는 방법에 대해 설명합니다. 연구자들은 ‘단계별 교차 검증’이라는 새로운 방법을 도입하여 스케일링 법칙의 성능을 철저히 검증했습니다.

단계별 교차 검증 방법

이 방법은 기존의 완전 교차 검증보다 계산 비용이 적으면서도 포괄적인 검증이 가능합니다. 주요 단계는 다음과 같습니다.

1. 임계값 조합
   • 데이터셋을 훈련 세트와 테스트 세트로 분할
   • 계산 효율성과 데이터 다양성의 균형을 위해 일정 간격으로 조합 선택
2. 훈련 및 테스트
   • 훈련 세트로 모델 학습, 검증 세트로 평가
   • Basinhopping 최적화 기법을 사용하여 스케일링 법칙의 최적 파라미터 탐색
3. 지수에 대한 L2 정규화 (α로 제어)
   • 지수 파라미터의 제곱합에 비례하는 페널티 항 추가
   • 큰 지수 값에 페널티를 부과하여 과적합 방지
4. 계수에 대한 L2 정규화 (β로 제어)
   • 계수 파라미터의 제곱합에 페널티 부과
   • 과도하게 큰 계수 값 방지
5. 모델 평가
   • RMSE(Root Mean Squared Error)와 MAE(Mean Absolute Error) 사용

이 방법을 통해 다양한 시나리오에서 모델의 성능을 철저히 조사하고, 스케일링 법칙 함수의 파라미터 선택에 대한 신뢰성을 확보할 수 있습니다.

정규화 파라미터 설정

연구자들은 다음과 같은 α와 β 값의 조합을 사용했습니다.

• α: [0.0, 0.01, 0.1, 1.0, 5.0, 10, 50]
• β: [0, 0.0001, 0.001, 0.01, 0.1]

결과 분석

Table 5는 가상 백과사전 데이터셋에 대한 다양한 스케일링 법칙 형태의 교차 검증 성능을 보이며, 주요 관찰 사항은 다음과 같습니다.

1. 가장 단순한 형태인 $L(p,f)=(a_0p^{-a_1}+a_2)f^{-a_3}+a_4$가 가장 낮은 RMSE와 MAE를 보인다.
2. 파인튜닝 데이터 항에 상수를 추가한 형태 (Index 2)가 약간 더 나은 RMSE를 보이지만, MAE는 더 높습니다.
3. pre-training dataset 항에 상수를 추가한 형태 (Index 3, 4)는 성능이 크게 떨어집니다.
4. 가장 단순한 형태에서 상수항을 제거한 모델 (Index 5)도 좋은 성능을 보입니다.

결론

이 분석을 통해 연구자들은 가장 단순한 형태의 스케일링 법칙이 데이터를 가장 잘 설명하면서도 과적합의 위험이 낮다는 결론을 내렸습니다. 이는 모델의 일반화 능력과 해석 가능성 측면에서 중요한 의미를 갖습니다.

이런 철저한 비교 분석은 제안된 스케일링 법칙의 신뢰성을 높이고, 향후 유사한 연구에서 참고할 수 있는 중요한 방법을 제시합니다.

Appendix E: 수렴까지의 에포크 수 분석

이 Appendix에서는 모델 학습 과정에서 수렴까지 필요한 에포크 수에 대한 분석 결과를 제시합니다. 연구자들은 사전 학습과 파인튜닝 데이터 크기가 수렴 속도에 미치는 영향을 조사했습니다.

주요 발견사항

1. 사전 학습의 영향
   • 사전 학습 정도가 높을수록 일반적으로 더 적은 에포크에서 수렴
   • 이는 검증 손실과 유사한 패턴을 보임
2. 파인튜닝 데이터 크기의 영향
   • 파인튜닝 데이터 크기와 수렴 에포크 수 사이의 관계는 명확하지 않음
   • 사전 학습과 달리 일관된 패턴을 보이지 않음
3. Early Stopping: Patience == 3
4. 사전 학습 단계와 파인튜닝 데이터 크기에 따른 수렴 에포크 수 변화 관찰
5. Figure 8을 통해 결과를 시각화
   • (a) 다양한 파인튜닝 데이터 크기에 대한 사전 학습 단계별 에포크 수 변화
   • (b) 사전 학습 단계별로 구분된 파인튜닝 데이터 크기에 따른 에포크 수 변화

결과 해석

1. 사전 학습의 효과
   • 더 많은 사전 학습은 모델이 더 빠르게 수렴하도록 함
   • 이는 사전 학습을 통해 모델이 더 좋은 초기 파라미터를 가지게 되어, 파인튜닝 시 더 적은 조정만으로도 좋은 성능에 도달할 수 있음을 시사
2. 파인튜닝 데이터 크기의 영향
   • 파인튜닝 데이터 크기와 수렴 속도 사이의 관계가 복잡함을 시사
   • 이는 데이터의 양뿐만 아니라 질, 다양성, 난이도 등 다양한 요인이 영향을 미칠 수 있음을 의미

결론 및 시사점

1. 효율적인 학습 전략
   • 충분한 사전 학습은 파인튜닝 시 학습 시간을 단축시킬 수 있음
   • 그러나 파인튜닝 데이터의 특성에 따라 최적의 전략이 달라질 수 있음
2. 향후 연구 방향
   • 파인튜닝 데이터의 특성이 수렴 속도에 미치는 영향에 대한 더 깊은 연구 필요
   • 사전 학습과 파인튜닝의 상호작용이 수렴 속도에 미치는 영향 연구

이 분석은 대규모 언어모델의 효율적인 학습 전략 수립에 중요한 통찰을 제공하며, 특히 계산 자원이 제한된 상황에서 모델 학습 시간을 최적화하는 데 도움을 줄 수 있습니다.

Appendix F: 각 데이터셋 설명 및 샘플

각 데이터셋에 대한 설명과 샘플

F.1 가상 백과사전

이 인공 데이터셋은 판타지 세계의 인물 전기를 담은 가상 백과사전으로 GPT-3.5를 사용하여 생성되었으며, 각 캐릭터의 특성은 Python으로 작성된 시뮬레이션 엔진에 의해 생성되었습니다. 이 데이터셋의 목적은 Pile에 없는 풍부하고 다양한 파인튜닝 데이터를 제공하여 트랜스포머 모델의 전이 학습 스케일링 법칙 구조를 테스트하는 것입니다.

Sample Data

Bel Elur was a prominent figure in the Orilune culture of Elyndorium. Born in the year 16 to parents Ylcar Siljorzor, an Elemental Aligned Chef, and El Ur, a Warlock, Bel's life was destined to be filled with both magic and gastronomy.

From an early age, Bel's potential as a spellcaster was evident. His eloquence and optimistic outlook on life made him a natural spell tutor, and he quickly became known for his profound knowledge and skill in teaching others the ways of magic. However, it was also his cruel streak that set him apart from his peers, and some questioned whether it was a necessary aspect of his nature or a mere result of his upbringing.



In the year 49, the weakened Orilune military forces faced further setbacks, which left the culture vulnerable to future conflicts. However, in the year 57, a glimmer of hope emerged as a member of the Orilune royalty married into Elandriel's esteemed royal family. This alliance strengthened the ties between the two cultures and offered a sense of security for the Orilune.

F.2 arXiv 수학

arXiv의 수학 카테고리에서 최근 논문들을 쿼리하고 LaTeX 형식으로 파싱한 데이터셋으로 Pythia 모델 학습 이후에 수집되어 pre-training dataset에 포함되지 않았을 가능성이 높습니다.

Sample Data

The purpose of this chapter is to give a rather exhaustive survey on the Maurer–Cartan equation and its related methods, which lie at the core of the present monograph. We first give a recollection of the Maurer–Cartan equation and its gauge symmetries in differential geometry. This chapter is viewed as a motivation for the rest of the book, which consists of higher algebraic generalisations of the key notions of gauge theory.



Throughout this chapter, various infinite series arise. For simplicity, we work with the strong assumption that the various differential graded Lie algebras are nilpotent, so that all these series are actually finite once evaluated on elements. We refer to the treatment of complete algebras given in the next chapter LABEL:sec:OptheoyFilMod for the correct setup in which convergence is understood in the rest of the text.

F.3 통계학 교과서

이 데이터셋은 John Fieberg의 “Statistics for Ecologists: A Frequentist and Bayesian Treatment of Modern Regression” 오픈소스 교과서에서 가져왔습니다. Pile 생성 이후에 출판되어 pre-training dataset에 포함되지 않았을 가능성이 높습니다.

Sample Data

Bootstrap procedure

If our sample data are representative of the population, as we generally assume when we have a large number of observations selected by simple random sampling, then we can use the distribution of values in our sample to approximate the distribution of values in the population. For example, we can make many copies of our sample data and use the resulting data set as an estimate of the whole population.



• A bootstrap distribution is the distribution of bootstrap statistics derived from many bootstrap samples. Whereas the sampling distribution will typically be centered on the population parameter, the bootstrap distribution will typically be centered on the sample statistic.2 That is OK, what we really want from a bootstrap distribution is a measure of variability from sample to sample.

F.4 고양이 게놈

이 데이터셋은 [felis_catus_9_ensemble]에서 가져온 고양이의 시퀀싱된 게놈입니다.

Sample Data

ATCAGGAGATCTAGATGCCTGGAGAGGAGTGGAGAAAACGGGAAACCCTCTTATGGGAAG
AGGTAATATGTATTTCTCCTTCGAATATAAAAAAAGTAAAAAGAAGGAAAACTTACCAAA
TTCACTTATGAGCCATTCATTACCCTGATACCAAAACCAGATAAAGCCCTCCACTAAAAC
CAAAACTGCAGCGGCGCCTTGTGGGCTCGGTCGGTTTTACTGTCCAACTCTTAATTTCAG
ATTAGGAAATAATCTTGCGGTGCATGGGTTCAAGTCCCACGTTGGACCCTGCCATGACAG

F.5 Enron 이메일

이 데이터셋은 잘 알려진 NLP 데이터셋인 Enron Emails 데이터셋의 일부입니다.

Sample Data

Message-ID: <2450437.1075860190764.JavaMail.evans@thyme>
Date: Wed, 14 Feb 2001 02:24:00 -0800 (PST)
From: mark.taylor@enron.com
Subject: New Canadian EOL Product
Mime-Version: 1.0
Content-Type: text/plain; charset=us-ascii
Content-Transfer-Encoding: 7bit
X-From: Mark Taylor
X-To:
X-cc:
X-bcc:
X-Folder: \Mark_Taylor_Jun2001\Notes Folders\All documents
X-Origin: Taylor-M
X-FileName: mtaylor.nsf

Greg:

2 Issues - an easy language issue and a more complicated regulatory issue.

First the easy one.