Google | Compute Optimal

• Related Project: Private
• Category: Paper Review
• Date: 2024-08-06

Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters

• url: https://arxiv.org/abs/2408.03314v1
• pdf: https://arxiv.org/pdf/2408.03314v1
• html: https://arxiv.org/html/2408.03314v1
• abstract: Enabling LLMs to improve their outputs by using more test-time computation is a critical step towards building generally self-improving agents that can operate on open-ended natural language. In this paper, we study the scaling of inference-time computation in LLMs, with a focus on answering the question: if an LLM is allowed to use a fixed but non-trivial amount of inference-time compute, how much can it improve its performance on a challenging prompt? Answering this question has implications not only on the achievable performance of LLMs, but also on the future of LLM pretraining and how one should tradeoff inference-time and pre-training compute. Despite its importance, little research attempted to understand the scaling behaviors of various test-time inference methods. Moreover, current work largely provides negative results for a number of these strategies. In this work, we analyze two primary mechanisms to scale test-time computation: (1) searching against dense, process-based verifier reward models; and (2) updating the model’s distribution over a response adaptively, given the prompt at test time. We find that in both cases, the effectiveness of different approaches to scaling test-time compute critically varies depending on the difficulty of the prompt. This observation motivates applying a “compute-optimal” scaling strategy, which acts to most effectively allocate test-time compute adaptively per prompt. Using this compute-optimal strategy, we can improve the efficiency of test-time compute scaling by more than 4x compared to a best-of-N baseline. Additionally, in a FLOPs-matched evaluation, we find that on problems where a smaller base model attains somewhat non-trivial success rates, test-time compute can be used to outperform a 14x larger model.

TL;DR

• LLM이 인퍼런스 시간에 추가 계산을 사용하여 성능을 얼마나 향상시킬 수 있는지를 집중적으로 탐색합니다.
• 검색 기반 검증 모델과 적응형 응답 분포 업데이트를 통해 성능을 비교합니다.
• 문제 난이도에 따라 테스트 시간 계산을 최적화하여 효율성을 높이는 방법을 제안합니다.

문제의 난이도를 분류한 뒤, 쉬운 문제는 인퍼런스 컴퓨트에 비용을 투자하고, 어려운 문제들은 Pre-training을 추가하는 것이 좋다.

논문에서는 LLMs(Large Language Models)가 테스트 시간에 추가적인 계산을 사용하여 그 성능을 향상시킬 수 있는지를 중심으로 확인합니다. 특히 문제의 난이도를 고려한 계산 자원의 최적화 배분에 중점을 둡니다.

• 테스트 시간 계산 확장의 효과 연구 결과에 따르면, LLM이 주어진 문제에 대해 추가 계산을 사용할 수 있게 하면, 프롬프트에 대해 모델의 성능을 상당히 향상시킬 수 있었다고 하며, 추가 계산은 다음 두 가지 메커니즘을 통해 사용합니다.
  • 검증기(Verifier)를 이용한 탐색: 이 방법은 과정 기반 보상 모델을 활용하여 답변의 정확성을 단계별로 검증하는 것으로, 각 단계의 예측을 통해 더 나은 답변을 선별할 수 있는 트리 탐색을 수행합니다. (쉬운 난이도의 과제는 Verifier가 충분히 잘 판단했다는 것이 경험적 인사이트였는데, 실험 결과도 동일했다고 하네요.)
  • 제안 분포(Proposal Distribution)의 수정: 모델이 자체적으로 답변을 수정하면서 반응 분포를 동적으로 개선하는 방법으로, 특히 잘못된 초기 응답을 수정하는 데 효과적으로 작동했다고 보고합니다.

핵심 파트

• 난이도에 따른 최적화 전략: 문제의 난이도에 따라 테스트 시간 계산의 확장 효과가 달랐습니다.
  • 쉬운 문제에서는 기본 모델이 이미 합리적인 응답을 생성할 수 있으므로 연속적인 수정이 더 효과적이었으나,
  • 어려운 문제는 다양한 접근 방식을 탐색하는 것이 더 유리했습니다.

• 계산 최적화 전략: 연구자들은 문제의 난이도를 평가하여 테스트 시간 계산을 최적화하는 전략을 개발하여, 각 문제의 난이도에 맞춰 가장 효과적인 계산 자원의 할당을 가능하게 했다고 합니다.

• 추가적인 테스트 시간 계산이 프리트레이닝을 대체할 수 있는지를 평가한 결과, 쉬운 및 중간 난이도의 문제에서는 테스트 시간 계산이 프리트레이닝을 대체하는 것이 약간 더 효과적이었습니다. 그러나 가장 어려운 문제에서는 추가적인 프리트레이닝 계산이 더 효과적이었습니다.

(사견이므로 무시) 러프하게 반환되는 여러가지 후보 중에 인퍼런스에 CoT를 적용해 가장 좋은 답변을 낼 수 있는 리워드 모델과 프롬프트 난이도를 분류할 수 있고, 판단할 수 있는 모델들로 프롬프트 난이도 별로 추가 프리트레이닝이나 SFT vs. 인퍼런스에 비용을 더 사용할 지에 대한 고찰

(사견이므로 무시) LeanGithub이나 기존 선행 연구들의 시도(CoT 혹은 최근 Meta의 리워딩 세부 과정에 NLP를 추가한 내용) 등을 고려하면, 이미 충분히 큰 모델들의 Pre-training의 학습은 충분했을 수 있고, Instruction Following과 같이 기존 지식들의 포맷을 정규화해서 지식들을 연결하거나 기존 지식을 기반으로 휴먼이 원하는 것(최근 MindSearch)을 반환하게 하는 작업 등이 필요할 수 있다는 것 같습니다. 결국 트랜스포머는 확률론적으로 Next Token을 잘 예측하는 것이고, Instrunction Tuning이나 CoT처럼 학습된 토큰들을 어떻게 잘 연결할 수 있는지에 대한 내용인 것 같습니다. 그리고 중간중간에 필요한 NLP 모델이나 알고리즘 등을 활용하는 것 역시 많은 분들이 공통적으로 갖고 있는 생각인 것 같습니다. 비싸고, 느린 LLM을 쉬운 태스크에까지 활용하는 것에 대한 것도 충분히 고려하면 좋을 것 같습니다. 인퍼런스 Trajectory와 관련된 내용들, NLP 태스크를 통해 더 효과적으로 학습하고 인퍼런스하는 내용들이 많은 것 같습니다.

1. 서론

현대의 대규모 언어모델(LLMs)이 복잡한 입력 쿼리에 효과적으로 대응할 수 있도록 추가 계산을 활용하는 방안을 제안합니다. 특히, 사전 훈련된 모델의 크기를 인퍼런스 시의 추가 계산으로 대체할 수 있는 가능성을 탐구함으로써, 모델의 유연성과 응용 가능성을 높이고자 합니다. 이런 추가 계산은 모델의 자체 개선 알고리즘으로서의 가능성을 제시하며, 휴먼의 의사 결정 과정에서 보이는 성찰을 모델에 적용할 수 있는 기반을 마련합니다.

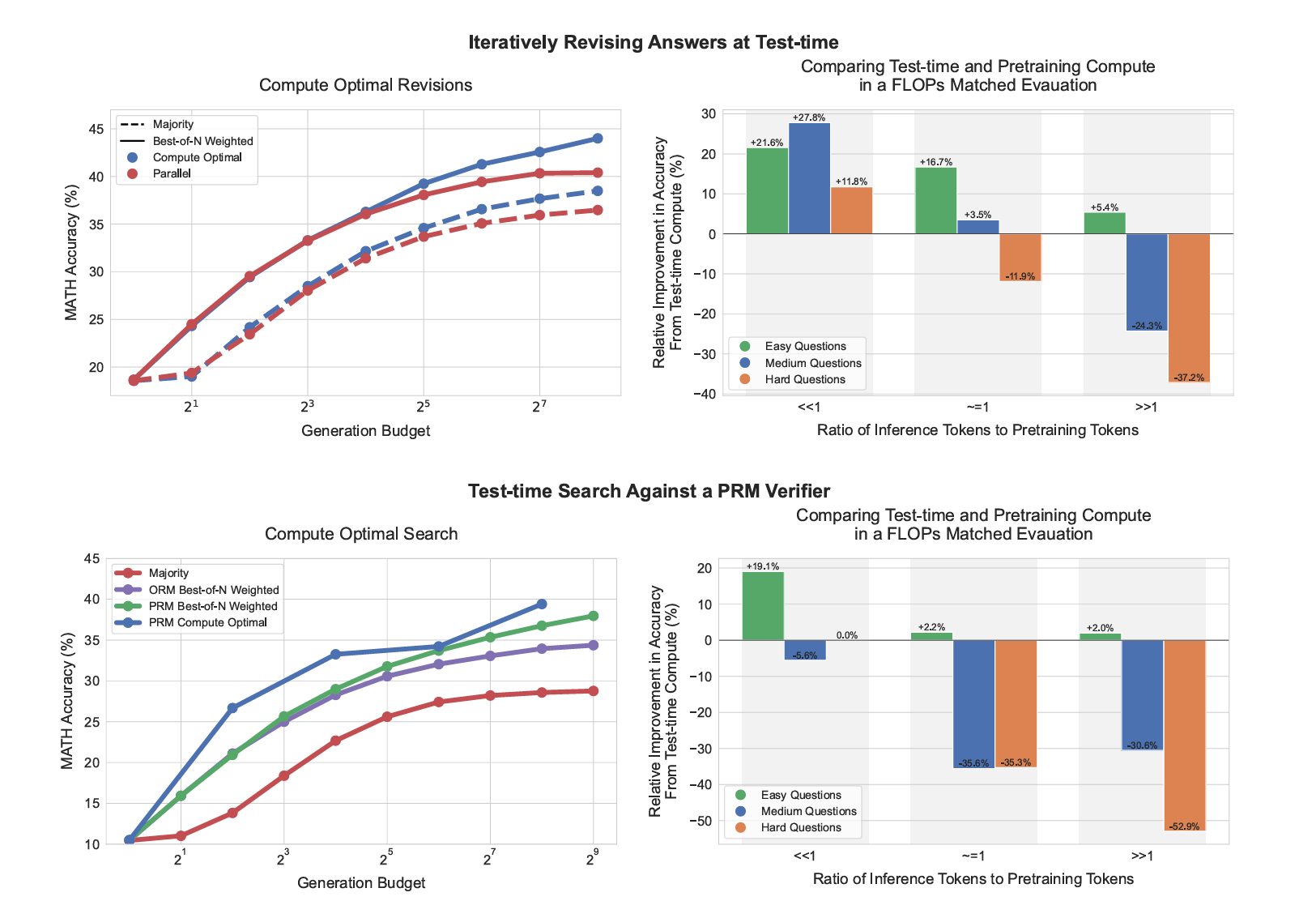
Figure 1은 본 논문의 전체적인 주요 결과를 요약합니다.

왼쪽 부분에서는 PaLM 2-S* 수정 모델의 계산 최적화 정책을 수정 설정(상단)과 PRM 검색 설정(하단)의 기준과 비교합니다. 수정 사례에서 표준 Best-of-$N$(e.g., “병렬”)과 계산 최적화 정책 간의 격차가 점차 확대되어 계산 최적화 정책이 테스트 시간 계산을 4배 적게 사용하면서도 Best-of-$N$ 성능을 초과하는 것을 볼 수 있습니다. PRM 검색 설정에서도 비슷하게 초기에 큰 개선을 보이며, 때때로 계산량이 4배 적은 상태에서 Best-of-$N$ 성능에 근접합니다.

오른쪽 부분에서는 계산 최적화된 테스트 시간의 성능과 더 큰 사전 학습 모델의 성능을 비교합니다. 두 모델 모두 사전 학습과 인퍼런스에 X, Y 토큰을 사용하는 설정을 고려합니다. 더 큰 모델을 학습하면 이 두 용어의 FLOPs 요구 사항이 배가됩니다. 만약 더 작은 모델에 추가적인 테스트 시간 계산을 적용하여 이 더 큰 모델의 FLOPs 요구 사항과 맞춘다면, 정확도 측면에서 어떻게 비교될까요? 수정(상단)의 경우 Y « X일 때, 테스트 시간 계산이 추가 사전 학습보다 선호되는 편입니다.

그러나 인퍼런스 대 사전 학습 토큰 비율이 증가함에 따라 쉬운 질문에서는 테스트 시간 계산이 계속 선호되지만, 어려운 질문에서는 이런 설정에서 사전 학습이 선호됩니다. PRM 검색(하단)에서도 비슷한 경향을 보입니다.

2. 테스트 시간 계산의 통합 관점: 제안자(Proposal)와 검증자(Verifier)

추가 테스트 시간 계산을 활용하는 두 가지 주요 방법을 소개하고 분석합니다. 첫 번째 방법은 주어진 프롬프트에 조건화된 모델의 예측 분포를 적응적으로 수정하는 것으로, 입력 수준에서 프롬프트에 추가 토큰을 제공하거나 출력 수준에서 여러 후보를 샘플링하여 수정하는 방식으로 진행됩니다.

이 과정은 복잡한 목표 분포에서 간단한 제안 분포와 점수 함수를 결합한 마르코프 체인 몬테 카를로(MCMC) 샘플링을 연상시킵니다.

참고자료 - 공돌이님의 수학노트

제안 분포 수정

제안 분포를 개선하는 방법으로, 모델을 특정 인퍼런스 작업에 최적화하거나 자기 비평을 통해 모델 스스로의 제안 분포를 테스트 시간에 개선하도록 합니다. 이는 복잡한 인퍼런스 기반 설정에서 모델이 자신의 답변을 반복적으로 수정하도록 하여 효과를 높입니다.

검증자 최적화

검증자는 제안된 분포에서 최적의 답변을 선택하는 데 사용됩니다. 기본적인 방법은 여러 완성된 솔루션을 샘플링한 후 최고의 솔루션을 선택하는 것입니다. 또한, 각 중간 단계의 정확성을 예측하는 프로세스 기반 검증자를 훈련시켜 트리 탐색을 통해 보다 효율적으로 검증자에 대항하여 탐색할 수 있습니다.

3. 테스트 시간 계산 최적화 방법

Problem setup

We are given a prompt and a test-time compute budget within which to solve the problem. Under the abstraction above, there are different ways to utilize test-time computation. Each of these methods may be more or less effective depending on the specific problem given. How can we determine the most effective way to utilize test-time compute for a given prompt? And how well would this do against simply utilizing a much bigger pretrained model?

이 섹션에서는 테스트 시간 계산을 최적화하여 주어진 프롬프트에 대한 언어 모델의 성능을 개선하는 방법을 모색합니다. 다양한 테스트 시간 계산 방법을 통합한 후, 이를 효과적으로 활용하는 방법을 이해하고자 합니다.

3.1 테스트 시간 계산 최적화 전략

테스트 시간 계산 예산을 주어진 문제에 대해 최적으로 할당하는 전략을 정의합니다. 이를 통해 주어진 프롬프트에서 모델이 생성한 자연어 출력 토큰의 분포를 최대화하는 하이퍼파라미터 $\theta$를 선택합니다. 수식으로는 다음과 같이 표현됩니다.

$y^*(q)$는 프롬프트 $q$에 대한 정확한 응답을 나타내며, \(\theta_{q, y^*(q)}^*(N)\)는 계산 예산 $N$을 가진 문제 $q$에 대한 테스트 시간 계산 최적화 전략을 나타냅니다.

3.2 문제 난이도 추정

테스트 집합에서 문제의 난이도를 추정하여 테스트 시간 계산 전략을 최적화합니다. 문제의 난이도는 모델의 pass@1 비율을 기준으로 하여 2048개의 샘플에서 계산된 통계를 사용하여 5개의 난이도 수준으로 분류합니다. 이렇게 추정된 난이도는 테스트 시간 계산 전략을 설계할 때 충분한 통계로 작용합니다.

이 연구는 LLMs의 테스트 시간 계산 확장성을 분석함으로써, 복잡한 프롬프트에 대한 모델의 응답 정확도를 향상시킬 수 있는 방법적 기반을 마련하고, 이를 통해 모델 성능의 개선 가능성을 탐구합니다.

4. 실험 설계

이 섹션에서는 다양한 검증자 설계 선택과 제안 분포에 대한 실험 설계를 개요하고, 후속 섹션에서 분석 결과를 제시합니다.

데이터셋

테스트 시간 계산은 모델이 문제에 대한 기본적인 ‘지식’을 이미 갖추고 있지만 복잡한 인퍼런스를 요구할 때 가장 도움이 됩니다. 이를 위해 고등학교 수준의 수학 문제를 포함하는 MATH 벤치마크[13]에 초점을 맞춥니다. 모든 실험에는 Lightman et al.[22]에서 사용된 12k 학습 및 500개의 테스트 질문으로 구성된 데이터셋 분할을 사용합니다.

모델

PaLM 2-S* [3] (Codey) 기본 모델을 사용하여 분석을 수행합니다. 이 모델은 현대의 많은 LLMs의 능력을 대표할 것으로 보이며, 따라서 발견이 유사한 모델에도 전달될 것으로 기대합니다. 가장 중요하게, 이 모델은 MATH에서 좋은 성능을 보였으나, 아직 포화 상태에 이르지 않았으므로 좋은 실험 대상이라고 생각하고 선정했다고 합니다.

5. 검증자를 통한 테스트 시간 계산 확장

이 섹션에서는 검증자를 최적화하여 테스트 시간 계산을 가능한 한 효과적으로 확장하는 방법을 분석합니다.

5.1 검증자 교육 및 탐색 가능하도록 만들기

PRM 교육. 원래 PRM 교육[42, 22]은 크라우드 워커의 레이블을 사용했습니다. Lightman et al.[22]이 PRM 교육 데이터(즉, PRM800k 데이터셋)를 공개했지만, 이 데이터는 저희에게 크게 효과적이지 않았습니다. PRM은 이 데이터셋에서 Best-of-$N$ 샘플링과 같은 단순한 전략을 이용하기 쉬웠습니다. 이는 GPT-4에서 생성된 샘플과 PaLM 2 모델 간의 분포 변화 때문일 가능성이 높습니다. PaLM 2 모델을 위해 비싼 크라우드 워커의 PRM 레이블을 수집하는 과정을 진행하기보다는, Wang et al.[45]의 접근 방식을 적용하여 휴먼 레이블 없이 PRM을 감독합니다.

PRM은 기본 모델의 샘플링 정책에 대한 보상으로 갈 때의 가치 추정치에 해당하는 각 단계의 정확성 추정치를 사용합니다.

ORM 베이스 라인과도 비교했지만(PR 보충 자료 F), PRM이 ORM보다 일관되게 우수한 성능을 보였습니다. 따라서 이 섹션의 모든 검색 실험에서 PRM 모델을 사용합니다. PRM 교육에 대한 추가 세부 정보는 Appendix D에서 확인할 수 있습니다.

답변 집계

테스트 시간에는 프로세스 기반 검증자를 사용하여 기본 모델에서 샘플링한 해결책 집합의 각 개별 단계를 평가할 수 있습니다. PRM을 사용하여 Best-of-$N$ 답변을 선택하려면 각 답변의 각 단계 점수를 집계하여 정확한 답변 후보를 결정할 수 있는 함수가 필요합니다. 이를 위해, 각 개별 답변의 단계별 점수를 집계하여 전체 답변에 대한 최종 점수를 얻습니다(단계별 집계). 그런 다음 답변 간에 집계하여 최고의 답변을 결정합니다(답변 간 집계). 구체적으로, 단계별 및 답변 간 집계를 다음과 같이 처리합니다.

• 단계별 집계: 단계 점수를 곱하거나 최소값을 취하는 대신, PRM의 마지막 단계 예측을 전체 답변 점수로 사용합니다. 이 방법이 연구한 모든 집계 방법 중에서 가장 잘 수행되는 것으로 나타났습니다(Appendix E 참조).
• 답변 간 집계: Li et al.[21]을 따라 표준 Best-of-$N$ 대신 ‘Best-of-$N$ 가중치’ 선택을 적용합니다. Best-of-$N$ 가중치 선택은 동일한 최종 답변을 가진 모든 솔루션의 검증자 정확성 점수를 소거하여 가장 큰 총합을 가진 최종 답변을 선택합니다.

5.2 PRM에 대한 검색 방법

PRM을 최적화하기 위해 테스트 시간에 검색 방법을 사용합니다. 몇 가지 검색 접근 방식을 연구합니다(Appendix G 참조). Figure 2에서 설명합니다.

• Best-of-$N$ 가중치: 기본 LLM에서 독립적으로 $N$개의 답변을 샘플링한 다음, PRM의 최종 답변 판단에 따라 최고의 답변을 선택합니다.

• Beam search: Beam search은 PRM의 단계별 예측을 검색하여 최적화합니다. 구현은 BFS-V[48, 10]와 유사합니다. 구체적으로, 고정된 수의 빔 N과 빔 폭 M을 고려합니다. 그런 다음 다음 단계를 실행합니다.

  1. 솔루션의 첫 번째 단계에 대해 $N$개의 초기 예측을 샘플링합니다.
  2. 생성된 단계를 PRM이 예측한 단계별 보상-대-가치 추정치(이는 접두어부터의 총 보상에도 해당됨)에 따라 점수를 매깁니다.
  3. 상위 $N$개의 가장 높은 점수를 받은 단계만 필터링합니다.
  4. 각 후보에서 다음 단계에 대한 M개의 제안을 샘플링하여 총 \(\frac{N}{M} \times M\) 후보 접두어를 다시 생성한 다음 2-4단계를 반복합니다.
  5. 이 알고리즘은 솔루션의 끝이나 빔 확장의 최대 라운드 수(본 논문의 경우 40)에 도달할 때까지 실행됩니다. 위에서 설명한 Best-of-$N$ 가중치 선택을 적용하여 최종 답변 예측을 결정합니다.

• Lookahead search: Lookahead search은 Beam search에서 개별 단계를 평가하는 방식을 수정합니다. $k$단계까지 선행 롤아웃을 수행하는 시뮬레이션을 실행하여 Beam search의 각 단계에서 PRM의 값 추정의 정확도를 개선합니다. 솔루션의 끝에 도달할 때까지 또는 선행 롤아웃이 끝날 때까지 멈추게 됩니다. 롤아웃의 분산을 최소화하기 위해 온도 0을 사용하여 롤아웃을 수행합니다. 이 롤아웃의 끝에서 PRM의 예측은 Beam search의 현재 단계를 점수 매기기 위해 사용됩니다. 즉, Lookahead search은 \(k = 0\) 인 경우의 Beam search의 특별한 경우로 볼 수 있습니다. 정확한 PRM을 사용한다면, \(k\)를 증가시키면 추가 계산 비용이 발생하더라도 각 단계의 값 추정의 정확성이 향상될 것입니다. 또한 이 Lookahead search 버전은 MCTS[38]의 특별한 경우로서, MCTS가 설계된 탐험을 촉진하는 확률적 요소들을 제거했기 때문에, 이미 훈련되어 있고 고정된 PRM을 사용할 때 테스트 시간에 적용되는 MCTS 스타일의 방법을 대표합니다. 이 확률적 요소들은 값 함수를 학습하는 데 유용하지만, 탐색보다는 활용을 원할 때 테스트 시간에는 덜 유용합니다. 따라서 Lookahead search은 주로 테스트 시간에 MCTS 스타일의 방법이 적용되는 방식을 대표합니다.

5.3 분석 결과: 검증자를 사용한 검색의 테스트 시간 계산 확장

이제 다양한 검색 알고리즘을 비교하고, 검색 방법에 대한 프롬프트 난이도 의존적인 계산 최적화 전략을 식별합니다.

검색 알고리즘 비교

다양한 검색 설정에 대해 실험을 수행합니다. 표준 Best-of-$N$ 접근 방식 외에도, 서로 다른 트리 검색 방법을 구분하는 두 주요 파라미터인 빔 폭 \(M\)과 선행 단계 수 \(k\)에 대해 실험을 진행합니다. 모든 설정을 철저하게 실험할 수는 없지만, 최대 256의 예산으로 다음 설정을 실험합니다.

1. 빔 폭이 \(N\)인 Beam search (\(N\)은 생성 예산)
2. 고정된 빔 폭 4를 사용하는 Beam search
3. Beam search 설정 1)과 2)에 \(k = 3\)을 적용한 Lookahead search
4. Beam search 설정 1)에 \(k = 1\)을 적용한 Lookahead search

검색 방법을 생성 예산의 기능으로 공정하게 비교하기 위해, 각 방법의 비용을 추정하는 프로토콜을 구축합니다. 기본 LLM에서 샘플링된 답변을 한 세대로 간주합니다. Beam search과 Best-of-$N$의 경우 생성 예산은 빔 수와 \(N\)에 해당합니다. 그러나 Lookahead search은 추가 계산을 사용합니다. 검색의 각 단계에서 \(k\) 추가 단계를 샘플링합니다. 따라서 Lookahead search의 비용을 \(N \times (k + 1)\) 샘플로 정의합니다.

결과

Figure 3(왼쪽)에 표시된 바와 같이, 작은 생성 예산에서는 Beam search이 Best-of-$N$을 크게 앞지릅니다. 그러나 예산이 확대되면 이런 개선이 크게 줄어들며, Beam search은 종종 Best-of-$N$ 기준을 밑돕니다. 또한 Lookahead search은 동일한 생성 예산에서 다른 방법보다 일반적으로 성능이 떨어지는데, 이는 선행 롤아웃을 시뮬레이션하는 데 추가 계산이 들어가기 때문입니다. 검색에서의 수익 감소는 PRM의 예측을 활용하는 결과로 볼 수 있습니다. 예를 들어, Figure 29에서 보듯이, 검색은 모델이 솔루션의 끝에서 정보가 거의 없는 반복적인 단계를 생성하게 합니다. 다른 경우에는, 검색이 과도하게 최적화되어 단지 1-2단계로 구성된 과도하게 짧은 솔루션을 결과로 낳습니다. 이는 가장 강력한 검색 방법인 Lookahead search이 가장 낮은 성능을 보이는 이유를 설명합니다. Appendix M에서 검색을 통해 발견된 여러 예를 포함했습니다.

문제 개선 방법

계산을 최적으로 확장하기 위해 어떤 문제가 검색을 개선하는지 이해하기 위해 난이도 빈 분석을 수행합니다. 구체적으로, \(M = 4\)인 Beam search과 Best-of-$N$을 비교합니다. Figure 3(오른쪽)에서 볼 수 있듯이, 높은 생성 예산으로 전체적으로 비슷한 성능을 보이는 Beam search과 Best-of-$N$을 평가하면, 난이도 빈을 통한 효과 평가는 다른 추세를 드러냅니다. 쉬운 질문(1과 2 레벨)에서는, 두 접근 방식 중 더 강력한 최적화자인 Beam search이 생성 예산이 증가함에 따라 성능이 저하되는 반면, Best-of-$N$은 그렇지 않습니다. 중간 난이도 문제(3과 4 레벨)에서는 Beam search이 일관되게 Best-of-$N$을 능가합니다.

그러나 가장 어려운 문제(5 레벨)에서는 어떤 방법도 의미 있는 진전을 보이지 않았습니다.

위 결과는 쉬운 질문에서는 검증자가 대부분 올바른 정확성 평가를 할 것으로 예상되었던 직관과도 일치합니다.

따라서 Beam search을 통해 추가 최적화를 적용하면, 검증자에 의해 학습된 잘못된 특성을 더욱 강화하여 성능 저하를 초래하는 반면 더 어려운 질문에서는 기본 모델이 처음부터 올바른 답변을 샘플링할 가능성이 훨씬 낮기 때문에, 검색은 모델이 올바른 답변을 더 자주 생성하도록 도울 수 있습니다.

이어서 4번 Figure의 설명과 계산 최적 검색에 대한 추가적인 논의를 진행합니다.

섹션 6에서는 제안된 분포의 수정을 통한 반복적인 모델 학습 및 개선 접근 방법을 논의하고, 섹션 7과 8에서는 예측 및 테스트 시간 계산의 교환에 대한 연구와 향후 연구 방향을 제시합니다.

6. 제안 분포의 수정

이 섹션에서는 검증자에 대한 검색과 대조하여 제안된 분포를 수정하는 모델의 확장 속성에 초점을 맞춥니다. 모델이 자체적인 오답을 반복적으로 수정하도록 하여, 테스트 시간에 자체 분포를 동적으로 개선할 수 있습니다.

6.1 설정: 수정 모델의 학습 및 사용

수정 모델의 파인튜닝 절차는 Qu et al. [28]의 방법에 기초하지만 몇 가지 중요한 차이점을 도입합니다. 파인튜닝을 위해서는, 일련의 틀린 답변 뒤에 정답이 오는 경로가 필요합니다. 이를 통해 모델은 제공된 컨텍스트에서 실수를 암시적으로 식별하고, 컨텍스트 예제를 무시하는 대신 수정을 통해 이 실수를 수정하는 방법을 효과적으로 학습합니다.

수정 데이터 생성은 Qu et al. [28]의 정책 기반 접근 방식에 따라 멀티턴 롤아웃을 얻는 것으로 입증되었으나, 인프라스트럭처의 제약으로 인해 완전히 실행 가능하지는 않았습니다. 따라서, 높은 온도에서 동시에 64개의 응답을 샘플링하고, 이 독립적인 샘플로부터 멀티턴 파인튜닝 데이터를 구성합니다.

6.2 분석 결과: 수정으로의 테스트 시간 확장

수정 모델을 사용할 때, 모델은 반복적으로 수정을 샘플링하여 각 단계에서 점점 개선된 결과를 보여주는 것으로 나타났습니다. 그러나 이런 수정은 훈련 시에만 사용된 틀린 답변의 컨텍스트에 국한되며, 테스트 시에는 정답이 포함될 수 있어 수정 단계에서 실수로 오답으로 변환될 위험이 있습니다. 이를 보완하기 위해, 순차적 다수결 투표 또는 검증자 기반 선택을 사용하여 모델이 만든 수정 시퀀스에서 가장 정확한 답변을 선택합니다.

이런 수정을 통해 제안된 분포의 수정이 검증된 답변을 선택하는 데 얼마나 효과적인지를 평가합니다. 연구 결과에 따르면, 순차적 샘플링이 병렬 샘플링보다 우수한 성능을 보여주는 것으로 나타났습니다. 이는 수정 모델이 이전 답변에서 발생한 실수로부터 학습하여 효과적으로 답변의 질을 개선할 수 있음을 시사합니다.

7. 예측 및 테스트 시간 계산의 교환

이 섹션에서는 예측 시의 추가 계산이 기본 LLM이 예측한 분포보다 복잡한 분포를 표현할 수 있게 함으로써 성능을 향상시킬 수 있음을 논의합니다. 주요 질문은, 모델이 사전 학습된 FLOPs와 테스트 시간 FLOPs를 교환하여 성능을 개선할 수 있는지 여부입니다.

연구 질문 및 실험

모델이 사전 학습된 \(X\) FLOPs와 함께 실행되고, 테스트 시 \(Y\) FLOPs를 사용할 계획이라면, 총 FLOPs 예산을 \(M\)배로 증가시키려면 이 FLOPs를 사전 학습 계산 또는 추가 테스트 시간 계산에 사용해야 합니다.

이 연구는 사전 학습과 테스트 시간의 FLOPs 사이에 교환 비율을 정의하는 방법을 설명합니다. 분석 결과, 쉬운 질문이나 작은 인퍼런스 요구 사항에서는 테스트 시간 계산이 추가 사전 학습을 보완할 수 있지만, 더 어려운 질문이나 높은 인퍼런스 요구 사항에서는 사전 학습이 성능을 개선하는 데 더 효과적입니다.

8. 토론 및 미래 작업

이 논문은 수정 모델을 통한 제안 분포의 개선이 어떻게 테스트 시간 계산을 최적화할 수 있는지에 대한 광범위한 논의를 제공합니다. 또한, 향후 연구를 위해 추가적인 데이터와 더 많은 파라미터를 동시에 확장하는 사전 학습 계산의 최적화 가능성을 탐구할 필요가 있음을 지적합니다.

[참고자료 1] 마르코프 체인 몬테카를로 (Markov Chain Monte Carlo, MCMC) 이해하기

1. 서론

선수지식

• Rejection Sampling: 샘플링 기법 중 하나로, 어떤 분포에서 무작위로 값을 뽑은 후, 해당 값을 수용할지 거부할지를 결정하는 과정
• Likelihood: 어떤 데이터가 특정한 확률 분포에서 나왔을 가능성을 나타내는 함수
• MCMC: 복잡한 분포에서 샘플을 추출하기 위한 방법

2. Monte Carlo 방법

2.1 Monte Carlo 방법이란?

Monte Carlo 방법은 무작위 샘플링을 사용하여 통계적 수치를 얻기 위한 일종의 시뮬레이션으로 많은 시도를 통해 실제 값을 추정할 수 있습니다. Monte Carlo 방법의 주요 목적은 무한히 많은 시도를 하지 않고도 현실적인 범위 내에서 정답을 추정하는 데 있습니다.

2.2 예시: 원의 넓이 계산

*출처: https://chi-feng.github.io/mcmc-demo/app.html?algorithm=HamiltonianMC&target=banana

이해를 돕기 위해 Monte Carlo 방법을 사용해서 원의 넓이를 계산하는 방법을 살펴보면, Monte Carlo 방법은 복잡한 수식을 풀기보다 무작위 시뮬레이션을 통해 결과를 얻는 방법임을 알 수 있습니다.

1. 정사각형 내의 무작위 점 찍기: 가로, 세로의 길이가 2인 정사각형 안에 무작위로 점을 찍습니다.
2. 원의 내부와 외부 구분: 중심에서부터의 거리가 1이하인 점(즉, 원의 내부에 있는 점)은 빨간색으로 칠하고, 그 외의 점은 파란색으로 칠합니다.
3. 비율 계산: 전체 점의 개수와 빨간색 점의 비율을 계산하여 원의 넓이를 추정합니다. 이 비율에 점들이 위치한 사각형 면적인 4를 곱하면 반지름이 1인 원의 넓이를 근사할 수 있습니다.

3. 마르코프 체인(Markov Chain)

3.1 Markov Chain의 기본 개념

Markov Chain은 현재 상태가 오직 직전 상태에만 영향을 받는 확률 과정을 의미합니다. 다시 말해, 미래 상태는 현재 상태에만 의존하고 그 이전의 상태들은 고려하지 않는 것을 의미하며, 많은 이론에서 한정된 계산 자원에서의 다음 단계로 넘어가기 위해 사용됩니다.

3.2 예시: 음식 선택

Markov Chain의 개념을 일상적인 예시로 생각해봅시다. 사람들이 전날 먹은 식사와 유사한 음식을 피하려는 경향이 있다고 가정하고, 어떤 사람이 어제 짜장면을 먹었다면 오늘은 중화요리 혹은 면 요리가 아닌 다른 음식을 먹을 가능성이 크다는 것을 의미합니다.

• 어제: 짜장면을 먹었다.
• 오늘: 중화, 면 요리가 아닌 다른 음식을 선택할 가능성이 더 높다.

이 경우, 오늘의 음식 선택은 어제의 음식 선택에만 영향을 받고, 그저께의 음식 선택은 고려되지 않습니다. 이런 과정을 Markov Chain이라고 합니다.

3.3 Markov Chain이 MCMC에서 어떻게 사용되는가?

MCMC에서 Markov Chain의 개념은 "마지막 샘플이 다음 샘플을 추천한다"는 의미로 주로 사용됩니다. 이전에 추출된 샘플이 다음 샘플을 결정하는 방식으로, 샘플링 과정이 진행됩니다.

4. MCMC를 이용한 샘플링

MCMC는 Monte Carlo 방법과 Markov Chain의 개념을 결합한 것으로, 복잡한 확률 분포에서 샘플을 추출하는 데 사용됩니다. 이 방법은 특히 베이지안 인퍼런스과 같은 분야에서 유용하게 사용됩니다.

4.1 샘플링 과정 (Metropolis 알고리즘)

MCMC의 샘플링 과정은 크게 네 단계로 나눌 수 있습니다. 이 과정은 MCMC의 대표적인 알고리즘인 Metropolis 알고리즘을 사용해 설명하겠습니다.

(1) 랜덤 초기화 (Random Initialization)

첫 번째 단계는 샘플 공간에서 임의의 초기값을 선택하는 것입니다. 예를 들어, \(x_0 = 7\)로 시작할 수 있습니다. 이 값은 타겟 분포와 관계없이 무작위로 선택됩니다.

(2) 제안 분포로부터 샘플 추천

다음 단계에서는 제안 분포(proposal distribution)를 사용해 다음 샘플을 추천받습니다. 제안 분포는 어떤 확률 분포를 사용해도 되지만, 대칭적인 분포인 정규분포를 자주 사용합니다.

• 제안 분포 그리기: 시작점 \(x_0\)를 중심으로 정규분포를 그리며, 표준편차는 연구자가 설정할 수 있습니다.
• 새로운 샘플 추출: 제안 분포에서 새로운 샘플 \(x_1\)을 추출합니다.

(3) 샘플 수용/거절 결정

세 번째 단계에서는 추출된 샘플을 수용할지 거절할지 결정하며, 타겟 분포 \(f(x)\)에서의 값을 비교해 이루어집니다.

• 수용: 새로운 샘플이 기존 샘플보다 타겟 분포에서 더 높은 값을 가지면, 즉 \(\frac{f(x_1)}{f(x_0)} > 1\)이면 새로운 샘플을 수용합니다.
• 거절: 그렇지 않을 경우, 패자부활전(다음 단계)에서 결정합니다. 주로 논문에서 Round로 표현됩니다.

4. 패자부활전

만약 수용 조건을 만족하지 않으면, 임의의 값 \(u\)를 사용해 확률적으로 샘플을 수용할지 거절할지 결정합니다.

\(u\)는 [0, 1] 범위에서 추출된 값이며, 이 과정을 통해 일부 거절된 샘플도 수용될 수 있습니다.

4.2 메트로폴리스-헤이스팅스 알고리즘

제안 분포가 대칭적이지 않을 때는 Metropolis 알고리즘을 확장한 Metropolis-Hastings 알고리즘을 사용합니다. 이 알고리즘은 제안 분포의 비대칭성을 고려하여 샘플을 수용할지 거절할지 결정합니다. (\(g(x)\)는 제안 분포)

Metropolis-Hastings 알고리즘은 이 비율을 사용해 샘플의 수용 여부를 판단합니다.

5. MCMC를 이용한 베이지안 추정 (Bayesian Estimation)

MCMC는 샘플링뿐만 아니라 베이지안 추정과 같은 파라미터 추정에도 사용될 수 있습니다. 예를 들어, 모집단의 평균이나 분산과 같은 파라미터를 추정할 수 있습니다.

5.1 파라미터 추정 과정

이제 MCMC를 사용해 파라미터 추정을 하는 과정을 설명하겠습니다.

(1) 랜덤 초기화

우선, 파라미터의 초기 값을 무작위로 설정합니다. 예를 들어, 평균 \(\mu\) 값을 1로 설정한 후, MCMC 알고리즘을 시작합니다.

(2) 제안 분포로부터 파라미터 추천

초기 설정된 평균 \(\mu_0\)를 기준으로 새로운 평균 값을 추천받습니다. 제안 분포로 정규분포를 사용하여 새로운 평균 \(\mu_1\)을 추출합니다.

(3) 제안 수용/거절

새로운 평균 \(\mu_1\)이 기존 평균 \(\mu_0\)보다 더 나은지 확인합니다. 이는 타겟 함수의 높이와 prior를 비교해 결정합니다.

• 베이지안 정리 사용: 베이지안 정리를 사용해 기존 파라미터와 새로운 파라미터를 비교합니다. 이 비교는 likelihood와 prior를 바탕으로 이루어집니다.

(4) 패자부활전

만약 새로운 평균 값이 거절되면, 패자부활전을 통해 확률적으로 수용할지 결정합니다.

\(u\)는 [0, 1] 범위에서 추출된 값입니다.

5.2 추정 결과

이 과정을 반복하여 여러 번의 시도 후, 초기의 값에서 점차 실제 모집단의 평균에 가까워지는 추정 결과를 얻을 수 있습니다. 이는 MCMC를 통해 데이터로부터 추정된 평균이 실제 평균에 수렴하는 과정입니다.

6. 결론

MCMC는 복잡한 확률 분포에서 샘플을 추출하거나 파라미터를 추정하는 데 유용하며, 특히 베이지안 인퍼런스과 같이 데이터의 불확실성을 반영해야 하는 문제에서 자주 사용됩니다.

[참고 자료]

1. 공돌이님의 수학노트
2. Github chi-feng/mcmc-demo