Scaling Filter**
- Related Project: Private
- Category: Paper Review
- Date: 2024-08-16
ScalingFilter: Assessing Data Quality through Inverse Utilization of Scaling Laws
- url: https://arxiv.org/abs/2408.08310
- pdf: https://arxiv.org/pdf/2408.08310
- html: https://arxiv.org/html/2408.08310v1
- abstract: High-quality data is crucial for the pre-training performance of large language models. Unfortunately, existing quality filtering methods rely on a known high-quality dataset as reference, which can introduce potential bias and compromise diversity. In this paper, we propose ScalingFilter, a novel approach that evaluates text quality based on the perplexity difference between two language models trained on the same data, thereby eliminating the influence of the reference dataset in the filtering process. An theoretical analysis shows that ScalingFilter is equivalent to an inverse utilization of scaling laws. Through training models with 1.3B parameters on the same data source processed by various quality filters, we find ScalingFilter can improve zero-shot performance of pre-trained models in downstream tasks. To assess the bias introduced by quality filtering, we introduce semantic diversity, a metric of utilizing text embedding models for semantic representations. Extensive experiments reveal that semantic diversity is a reliable indicator of dataset diversity, and ScalingFilter achieves an optimal balance between downstream performance and semantic diversity.
[Data Preprocessing Filtering 색인마킹]
TL;DR
- 데이터 품질 평가를 위한 ScalingFilter 제안: 모델 스케일링 법칙을 역이용하여 데이터 품질을 평가하는 새로운 방법 도입
- 모델 간 Perplexity 차이 분석: 서로 다른 크기의 모델들이 동일한 데이터에 대해 산출한 Perplexity 차이를 기반으로 데이터 품질을 평가
- 데이터 다양성 보존 및 성능 향상: 기존 필터링 방법들과 비교해 데이터 다양성을 더 잘 보존하면서도 성능을 향상시킴
- ScalingFilter는 참조 데이터셋에 의존하지 않고, 서로 다른 크기의 언어 모델 간의 Perplexity 차이를 이용해 데이터 품질을 평가합니다. 이는 참조 데이터가 가져올 수 있는 편향을 제거하고, 훈련 데이터의 다양성과 대표성을 높이는 데 기여하였다고 평가합니다.
- Perplexity 차이를 활용한 품질 계수(quality factor)는 데이터 품질과 긍정적인 상관관계를 가집니다. 이 품질 계수를 사용하여 고품질 데이터를 선택함으로써, 모델의 zero-shot 성능을 향상시킬 수 있었다고 보고합니다. (경험적으로 제로-샷은 SFT 데이터 퀄리티에 의존하는 경향이 있는 것 같습니다. 퓨-샷은 전반적인 논리적인 연결고리(e.g. CoT)를 제대로 산입하거나 보간하는 것이 중요한 것 같다고 느꼈습니다.)
- ScalingFilter는 데이터셋의 의미론적 다양성을 평가하고 보존하는 데 효과적이라고 언급하며, 다양한 주제와 글쓰기 스타일을 포함하는 데이터를 유지함으로써 모델의 예측 능력과 일반화 성능을 높이는 데 기여했다고 합니다.
- 스케일링 법칙을 역으로 활용하여 Perplexity 차이를 기반으로 데이터 품질을 평가하는 방법을 도입했습니다. 이를 통해 모델 크기와 데이터 크기의 최적 비율을 찾고, 높은 품질의 데이터를 효과적으로 선별할 수 있었다고 보고합니다.
- ScalingFilter로 필터링된 데이터로 학습된 모델은 다양한 downstream 작업에서 기존 방법보다 우수한 성능을 보여 고품질 데이터가 모델 성능에 직접적인 영향을 미친다는 점을 확인합니다.
[SFT Data Quality 데이터 퀄리티에 따른 Zero-shot 인퍼런스 성능 향상 색인마킹]
1. 도입
대규모 언어모델(LLMs)의 성공은 사전 학습에 사용되는 데이터셋의 품질과 양에 크게 의존합니다. 연구자들은 데이터셋 품질을 높이기 위해 다양한 데이터 큐레이션 파이프라인을 개발했으며, 그 중 핵심은 웹 크롤링, 텍스트 추출, 중복 제거 및 유해한 콘텐츠 제거, 그리고 품질 필터링입니다 (Brown et al., 2020; Rae et al., 2021; Penedo et al., 2023).
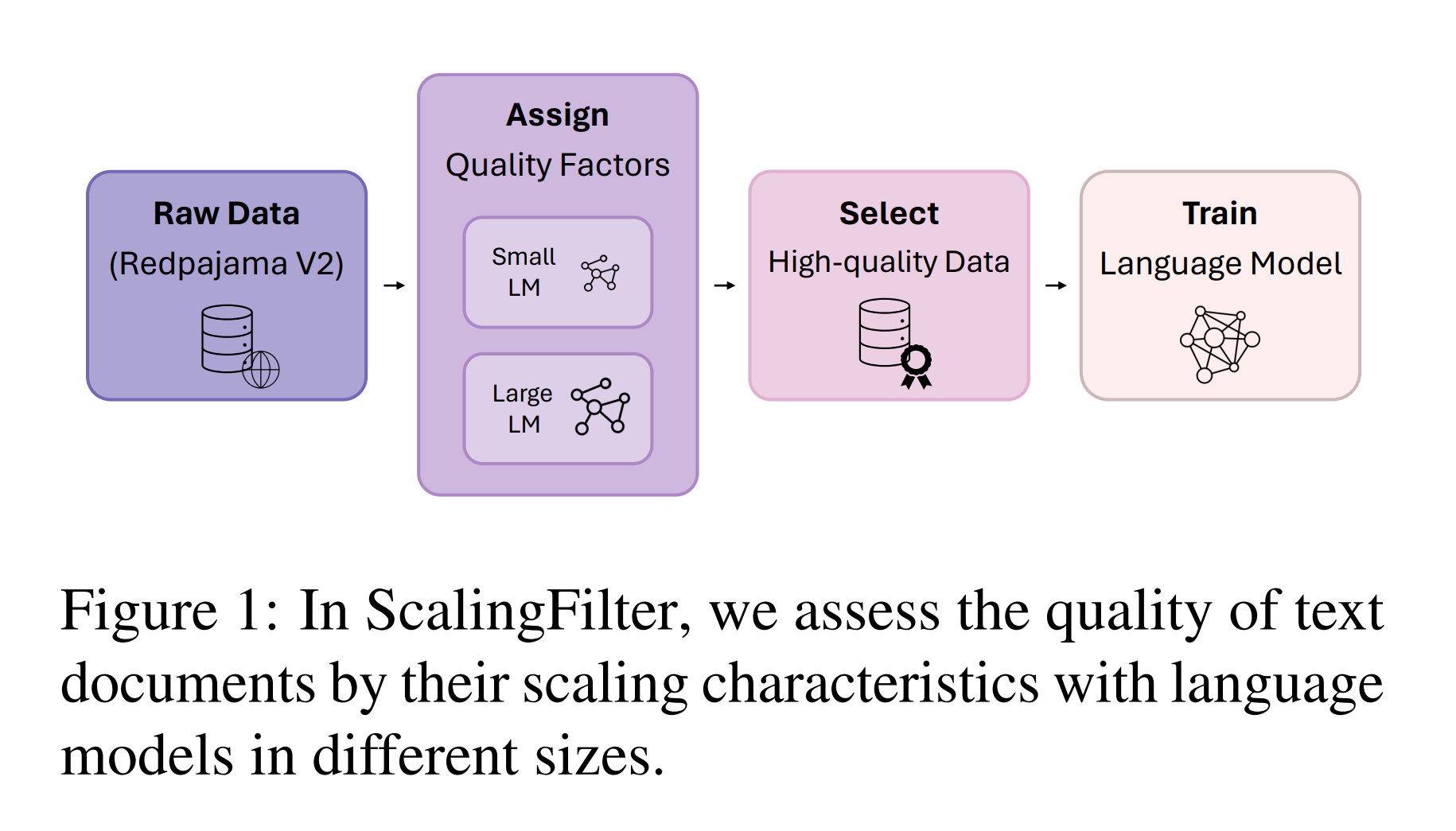
품질 필터링은 노이즈가 많은 원시 코퍼스에서 고품질 데이터를 추출하여 모델 성능을 높이는 데 목적이 있습니다.
기존의 품질 필터링 방법은 크게 (1) 참조 의존적 방법(reference-dependent methods)과 (2) 참조 독립적 방법(reference-free methods)으로 나눌 수 있습니다.
- (1) 참조 의존적 방법(Reference-dependent Methods)은 고품질의 시드 데이터셋과 비교하여 저품질 데이터를 필터링합니다. 이 방법은 필터링 성능은 뛰어나지만, 시드 데이터셋의 편향성을 고스란히 반영하여 training dataset의 다양성과 대표성을 제한할 수 있습니다.
- (2) 참조 독립적 방법(Reference-free Methods)은 사전 정의된 기준을 사용하여 데이터 품질을 평가합니다. 예를 들어, Perplexity 게이팅(perplexity gating)은 사전 학습된 모델의 Perplexity 점수를 사용합니다. 그러나 이 방법은 Perplexity와 문서 품질 사이의 간접적인 관계로 인해 단순하고 반복적인 콘텐츠가 유리하게 평가되는 문제를 안고 있습니다.
2. ScalingFilter 방법
이런 문제를 해결하기 위해 ScalingFilter라는 간단하면서도 효과적인 품질 필터링 방법을 제안합니다. 이 방법은 생성 모델링에서 최근의 스케일링 법칙(scaling laws)을 역으로 활용하여 데이터 품질을 평가합니다. 기본 아이디어는 동일한 데이터에 대해 두 개의 서로 다른 크기의 사전 학습 모델의 Perplexity 차이를 분석하는 것입니다. 이런 Perplexity 차이와 데이터 품질 사이의 긍정적인 상관관계를 Chinchilla 스케일링 법칙(Hoffmann et al., 2022)을 역으로 유도하여 발견했습니다.
\[\text{Perplexity Difference} = P_{\text{large}}(d) - P_{\text{small}}(d)\]$P_{\text{large}}(d)$와 $P_{\text{small}}(d)$는 각각 큰 모델과 작은 모델이 문서 $d$에 대해 계산한 Perplexity로 차이가 클수록 해당 문서의 품질이 높다고 평가할 수 있습니다.
ScalingFilter는 두 모델 간의 Perplexity 차이를 활용함으로써 단일 모델에 의존하여 발생할 수 있는 편향 문제를 효과적으로 해결합니다. 또한, 단순하고 반복적인 텍스트가 과도하게 선택되는 문제를 완화하여 데이터의 다양성과 복잡성을 높이는 데 기여하고자 합니다. 이 접근 방식은 Perplexity 차이를 데이터 필터링의 품질 지표로 사용하는 이론적 분석도 제공합니다.
개요 (Overview)
기존의 품질 필터링 방법은 고품질의 참조 데이터셋에 의존하거나, 단일 언어 모델의 절대적인 Perplexity 점수를 사용하여 필터링을 수행합니다. 그러나 이런 접근 방식은 잠재적인 편향을 유발하거나 성능 저하를 초래할 수 있습니다. 이 섹션에서는 ScalingFilter의 원리를 수학적 유도를 통해 자세히 설명하겠습니다. ScalingFilter의 핵심 개념은 스케일링 법칙(scaling law)을 역으로 적용하여 데이터 샘플의 품질을 추정하는 데 있습니다. 스케일링 법칙은 모델 크기나 데이터 크기가 증가함에 따라 손실(loss)이 멱법칙(power-law)으로 감소한다는 것을 보여줍니다 (Hestness et al., 2017; Kaplan et al., 2020; Hoffmann et al., 2022; Aghajanyan et al., 2023). 이 법칙은 동일한 계산 예산(TFLOPS) 내에서 모델 크기와 훈련 토큰 수의 최적 비율을 결정하여 최저 손실을 달성하는 전략을 제공합니다.
여러 데이터셋 간의 비교 실험을 통해 고품질 데이터는 모델 스케일링 지수 $a$를 증가시킨다는 사실이 밝혀졌습니다 (Bi et al., 2024). 특히, 초기와 최종 버전의 사내 데이터 및 OpenWebText2 (Gao et al., 2020)를 비교한 실험에서, 최종 버전의 OpenWebText2가 가장 높은 $a$ 값을 보였으며, 초기 버전은 가장 낮은 $a$ 값을 나타냈습니다. 이로부터 $a$ 값이 클수록 모델 파라미터가 증가함에 따라 손실 감소 속도가 더 빨라진다는 긍정적인 상관관계를 인퍼런스할 수 있습니다. 이런 관찰은 고품질 데이터가 논리적 명확성을 높이고, 충분한 훈련 후 예측 난이도를 낮추며, 결과적으로 계산 예산이 증가할 때 모델 크기 확장이 더 유리해짐을 시사합니다.
이 원리를 역으로 적용하여, ScalingFilter는 고정된 파라미터 차이를 가진 모델에서 손실 감소율을 기반으로 데이터 품질을 추정하고, 이를 통해 원시 데이터셋에서 고품질 데이터를 분리합니다.
품질 계수 (Quality Factor)
먼저 품질 계수(quality factor)를 정의하고, 이 계수와 데이터 품질 간의 긍정적인 상관관계를 입증하겠습니다. 작은 메타 모델을 $p$로, 큰 메타 모델을 $q$로 표기하겠습니다. 이 두 메타 모델은 동일한 아키텍처를 공유하며, 동일한 데이터셋에서 훈련되었지만, 파라미터 수 $N_p$와 $N_q$의 차이만 존재합니다 ($N_p < N_q$). 주어진 텍스트 샘플 $x_i$에 대한 품질 계수 $d_i$를 다음과 같이 정의할 수 있습니다.
\[d_i := \frac{PPL_p(x_i)}{PPL_q(x_i)}\]$PPL_p(x_i)$와 $PPL_q(x_i)$는 각각 $p$와 $q$ 모델이 텍스트 샘플 $x_i$에 대해 계산한 Perplexity 점수를 나타냅니다. Perplexity는 교차 엔트로피 손실(cross-entropy loss) $L$과 직접적인 관계가 있으며, $PPL = 2^L$로 나타낼 수 있습니다. 이는 Perplexity 점수가 손실 $L$과 양의 상관관계가 있음을 의미합니다.
품질 계수와 데이터 품질의 상관관계
다음으로 스케일링 법칙의 표현을 도입하고, 이를 모델 스케일링 지수 $a$와 연관시키는 형태로 변환합니다. 이를 통해 데이터 품질과 $a$ 값 사이의 긍정적인 상관관계를 통해 입증할 수 있습니다 (Bi et al., 2024).
모델 파라미터 수 $N$과 훈련 토큰 수 $D$가 주어졌을 때, 예상되는 모델 손실 $L^{\hat{}}$은 다음과 같이 수식화됩니다. (Hoffmann et al., 2022)
\[L^{\hat{}}(N, D) = E + A N^{\alpha} + B D^{\beta}\]$E$는 자연어 텍스트의 엔트로피에 해당하는 최소한의 손실을 나타내며, $A N^{\alpha}$와 $B D^{\beta}$는 각각 함수 근사 오차와 최적화 혹은 수렴 오차를 고려한 항입니다 (Aghajanyan et al., 2023). 이 스케일링 법칙은 주어진 계산 예산 $C$ 하에서 최적화된 $N$과 $D$의 수를 다음과 같은 멱법칙 형태로 따릅니다. (Kaplan et al., 2020; Hoffmann et al., 2022)
\[N_{\text{opt}} \propto C^{a}, \quad D_{\text{opt}} \propto C^{b}\]$a = \frac{\beta}{\alpha + \beta}$와 $b = \frac{\alpha}{\alpha + \beta}$는 각각 모델 스케일링 지수와 데이터 스케일링 지수를 나타내며, 이는 최적의 계산 할당에서 모델 스케일링과 데이터 스케일링에 할당되는 비율을 나타냅니다.
이제 $\eta \equiv \alpha + \beta$라고 설정하면, $L^{\hat{}}$은 다음과 같이 표현할 수 있습니다.
\[L^{\hat{}}(N, D) = E + A N^{(1 - a)\eta} + B D^{a \eta}\]$L^{\hat{}}$과 모델 스케일링 지수 $a$ 및 모델 크기 $N$ 사이의 관계에 집중할 것이며, 따라서 $L^{\hat{}}$을 $L^{\hat{}}(a, N)$으로 나타낼 수 있습니다.
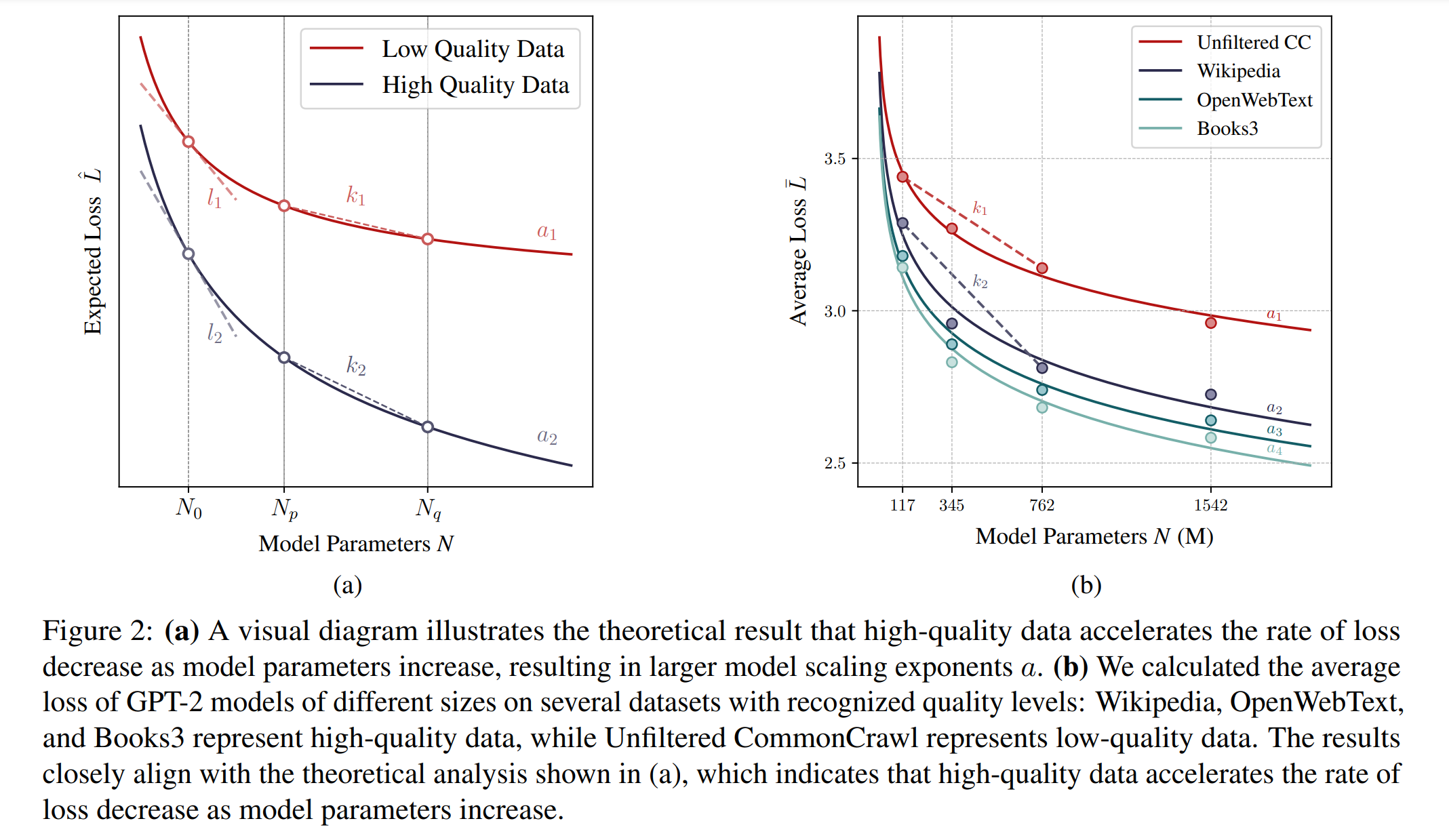
모델 크기 $N$이 증가함에 따라 $L^{\hat{}}$가 감소하는 것은 명백합니다. Appendix A.2.1에서 특정 $N_0$에서 접선의 기울기가 $a$ 값이 증가함에 따라 감소함을 증명합니다. 즉, $a$가 클수록 접선이 더 가파르며, 이는 Figure 2(a)에 나타난 바와 같이 $l_2$가 $l_1$보다 더 가파르다는 것을 보여줍니다. 이런 단조 관계를 통해 $a$ 값을 접선의 기울기로부터 유추할 수 있습니다. 주어진 $N_0$에서 더 가파른 접선(기울기의 절대값이 더 큼)은 더 큰 $a$ 값을 나타냅니다. 즉,
\[a \propto -\frac{\partial L}{\partial N} \Big|_{N = N_0}\]또한, Appendix A.2.2에서 위의 결론이 주어진 $\Delta N$ (즉, Figure 2(a)의 $k_i$)에 대해 접선 기울기에서 초선을 이룰 수 있음을 증명합니다. \(\Delta N = N_q - N_p\)로 설정할 때, 초선의 기울기는 항상 음수이며, $a$는 초선 기울기의 음수와 양의 상관관계를 가집니다. 품질 계수 $d$ 또한 초선 기울기의 음수와 양의 상관관계를 가지므로, $d$는 $a$와 양의 상관관계를 가집니다.
\[\left\{ \begin{aligned} a &\propto -\frac{L^{\hat{}}(N_q) - L^{\hat{}}(N_p)}{N_q - N_p}, \\ d &= 2^{L^{\hat{}}(N_q) - L^{\hat{}}(N_p)} \\ \Rightarrow \, d &\propto 2^{-a} \end{aligned} \right.\]- 첫 번째 수식에서 $a$는 기울기와 반비례 관계에 있으므로 $a \propto -\frac{L^{\hat{}}(N_q) - L^{\hat{}}(N_p)}{N_q - N_p}$
- 두 번째 수식에서 $d$는 Perplexity 차이의 로그 기반 지표로 정의되므로, $2^{L^{\hat{}}(N_q) - L^{\hat{}}(N_p)}$로 표현
- 마지막으로, $d$는 $2^{-a}$에 비례
(Bi et al., 2024)의 실험적 관찰에 따르면, 높은 $a$ 값은 고품질 데이터를 통해 달성되며, 이는 품질 계수 $d$가 데이터 품질과 양의 상관관계를 가진다는 결론을 이끌어낼 수 있습니다.
이 결론은 실질적인 비교 테스트와 일치합니다. Figure 2(b)에 나타난 바와 같이, GPT-2 모델의 서로 다른 크기를 사용하여 Wikipedia, OpenWebText, Books3와 같은 고품질 데이터셋과 Unfiltered CommonCrawl과 같은 저품질 데이터셋에서 평균 손실을 계산했습니다. 결과는 Figure 2(a)의 이론적 추정치와 밀접하게 일치했으며, 고품질 데이터는 저품질 데이터보다 더 가파른 초선($k_2 > k_1$)을 보였습니다. 단일 케이스는 메타 모델의 훈련 데이터 분포에서 벗어나 다양한 모델 크기에 대해 더 높은 절대 Perplexity를 유발할 수 있음을 주목할 필요가 있습니다. 그러나 Perplexity가 모델 파라미터 증가에 따라 더 크게 감소하는 법칙을 따르므로, 고품질 데이터는 더 큰 Perplexity 차이(즉, 품질 계수)를 나타냅니다.
품질 계수를 활용한 고품질 데이터 선택
위에서 설명한 바와 같이, 품질 계수는 데이터 품질을 직접적으로 나타낼 수 있으며, 이를 사용하여 노이즈가 있는 필터링되지 않은 데이터셋에서 고품질 데이터를 선택할 수 있습니다. 이 간단하면서도 효과적인 방법을 ScalingFilter라고 부릅니다. Figure 1에 나타난 바와 같이, 고품질 및 저품질 문서를 모두 포함하는 필터링되지 않은 문서 집합 $\mathcal{S}$을 고려하십시오. 각 샘플 $x_i \in \mathcal{S}$에 대해 품질 계수 $d_i$를 계산합니다. 앞서 도출한 바와 같이, $d_i$ 값이 클수록 해당 샘플의 품질이 더 우수합니다. 그런 다음, 상위-$k$ 샘플을 원하는 클리닝 비율에 따라 선택하여 최종 데이터셋을 구성합니다.
3. 실험 및 결과
- ScalingFilter로 필터링된 데이터셋이 다양한 downstream 작업에서 일관되게 높은 성능을 발휘함을 입증
- 고품질 데이터셋은 모델 성능뿐만 아니라 데이터의 의미론적 다양성도 보존함을 확인
- 다양한 품질 필터링 방법과 비교하여 ScalingFilter의 우수성을 수학적, 실험적으로 증명
ScalingFilter의 효과 검증
본 실험에서는 ScalingFilter의 효과를 다각도로 검증합니다. 특히 ScalingFilter로 필터링된 데이터를 기반으로 학습된 언어 모델들이 다양한 downstream 작업에서 높은 성능을 기록했음을 확인했습니다. 이는 필터링된 데이터의 품질이 높음을 나타내며, ScalingFilter의 장점을 보여줍니다.
ScalingFilter가 기존 방법들보다 필터링된 데이터의 품질을 더 잘 개선하면서도 데이터의 다양성을 유지하는 데 우수함을 실험을 통해 입증했습니다. 구체적으로, 124M과 774M 파라미터를 가진 두 메타 모델을 사용하여 원시 데이터셋의 각 문서에 대해 Perplexity 차이를 계산하고, 이를 기반으로 상위 k%의 고품질 문서를 선택했습니다. 이후 필터링된 고품질 데이터를 사용하여 1.3B 모델을 처음부터 학습시키고, downstream 작업에서의 성능과 필터링된 데이터셋의 의미론적 다양성을 평가했습니다.
실험 결과, ScalingFilter는 기존 SoTA 품질 필터링 방법을 능가하는 성능을 보였습니다. Perplexity 게이팅과 비교했을 때, 성능은 +1.12%, 의미론적 다양성은 +4.7만큼 개선되었다고 합니다.
3.1 데이터 품질 평가 (Data Quality Evaluation)
실험 설정 (Setup)
먼저, 2019년부터 2023년까지의 CommonCrawl 데이터 덤프에서 CCNet (Wenzek et al., 2019) 파이프라인을 통해 전처리된 데이터셋을 사용하여 실험을 진행했습니다. 약 500GB의 텍스트 데이터를 무작위로 선택하여 약 1250억 개의 토큰을 포함하는 기본 데이터셋을 구축하고, 추가적인 품질 필터링을 수행했습니다. 각 실험에서는 1.3B 파라미터를 가진 decoder-only 모델을 동일한 아키텍처로 학습시켰으며, 이는 (Peng et al., 2023)의 모델과 동일한 아키텍처입니다. 모델은 약 25B 토큰에 대해 학습되었으며, 성능이 안정화될 때까지 학습을 지속했습니다. 이런 학습은 (Hoffmann et al., 2022; Penedo et al., 2023; Marion et al., 2023)에 따라 약 4일간 4개의 노드와 8개의 NVIDIA Tesla V100 GPU를 사용하여 진행되었습니다.
모든 실험에서 품질 계수를 계산하기 위해 사전 학습된 GPT-2 모델 (Radford et al., 2019)을 메타 모델로 사용했습니다. 작은 모델은 124M 파라미터를, 큰 모델은 774M 파라미터를 가지고 있으며, 이후 메타 모델의 training dataset에 따른 영향에 대해 다양한 ablation 연구를 수행했습니다. 각 모델은 lm-evaluation-harness 라이브러리 (Gao et al., 2023)를 사용하여 다양한 downstream 작업에 대한 zero-shot 성능을 평가했습니다.
비교군 설정 (Baselines)
ScalingFilter는 무작위 선택(random selection), 이진 분류(binary classification) (Brown et al., 2020; Gao et al., 2020; Chowdhery et al., 2023; Touvron et al., 2023), 중요도 재표집(importance resampling) (Xie et al., 2023) 및 Perplexity 게이팅(perplexity gating) (Marion et al., 2023)과 비교했습니다. 모든 품질 필터링 방법은 (Computer, 2023)에 맞춰 필터링되지 않은 문서의 70%를 유지하도록 설정했습니다. 이진 분류의 경우 Wikipedia, books, OpenWebText를 양성 샘플로, 필터링되지 않은 CommonCrawl 문서를 음성 샘플로 사용했습니다. 중요도 재표집은 (Xie et al., 2023)의 설정을 따랐으며, 목표 데이터셋으로 OpenWebText (Gokaslan and Cohen, 2019)를 사용했습니다. Perplexity 게이팅은 (Marion et al., 2023)과 클리닝 비율을 따라 문서의 Perplexity 점수가 15%에서 85% 범위에 있는 문서만 유지했습니다.
결과
표 1에서는 다양한 데이터 품질 필터링 방법들 간의 성능 비교를 보여줍니다.
- ScalingFilter는 평균적으로 널리 사용되는 이진 분류 품질 필터링 방법보다 0.62% 더 우수한 성능을 보였으며, 중요도 재표집보다 0.73% 더 우수한 성능을 기록했습니다.
- Perplexity 게이팅보다 평균 정확도가 1.12% 더 향상되었습니다.
이진 분류와 중요도 재표집은 OpenWebText를 참조 데이터셋으로 사용했으며, Perplexity 게이팅은 메타 모델 중 더 큰 모델의 Perplexity 점수를 사용해 공정한 비교를 수행했습니다.
메타 모델 training dataset의 효과에 대한 Ablation 연구
표 2는 ScalingFilter 프레임워크 내에서 메타 모델의 training dataset가 성능에 미치는 영향을 보여줍니다. WebText 이외의 다양한 데이터셋으로 학습된 메타 모델도 경쟁력 있는 성능을 보였으며, 이는 ScalingFilter의 견고성과 유연성을 강조합니다.
3.2 데이터 다양성 평가 (Data Diversity Evaluation)
대규모 언어모델 학습에는 다양한 데이터가 필요합니다. 현재의 품질 필터는 참조 데이터셋과 유사한 텍스트 데이터를 선호함으로써, 비공식적 주제나 소수자 문서들을 폐기하여 모델의 지식 다양성을 감소시킬 수 있습니다 (Wenzek et al., 2019; Soldaini et al., 2023).
의미론적 다양성 지표 (Semantic Diversity Metric)
(Friedman and Dieng, 2022)를 참고하여, 의미론적 다양성은 의미론적 유사성 행렬의 고유값의 샤논 엔트로피(Shannon entropy)의 지수로 정의됩니다. 주어진 텍스트 문서 집합 $x_1, x_2, \ldots, x_n$과 의미론적 유사성 함수 $f$에 대해, 유사성 행렬 $\mathbf{S}$을 얻습니다. 행렬의 각 항목은 $s_{i,j} = f(x_i, x_j)$로 나타낼 수 있습니다. 고유값 $\lambda_1, \lambda_2, \ldots, \lambda_n$을 사용하여 의미론적 다양성을 다음과 같이 정의합니다.
\[\text{SemanticDiversity} = \exp\left(-\sum_{i=1}^{n} \lambda_i \log \lambda_i \right)\]각 문서의 의미론적 임베딩을 추출하기 위해 사전 학습된 언어 모델을 사용하고, 유사성 함수로는 코사인 유사성을 사용했습니다. 실험에서는 bge-base-en-v1.5 모델 (Xiao et al., 2023)을 sentence_transformers 라이브러리와 함께 사용했습니다.
문서의 적절한 크기 선택 (Selecting a Proper Size of Documents)
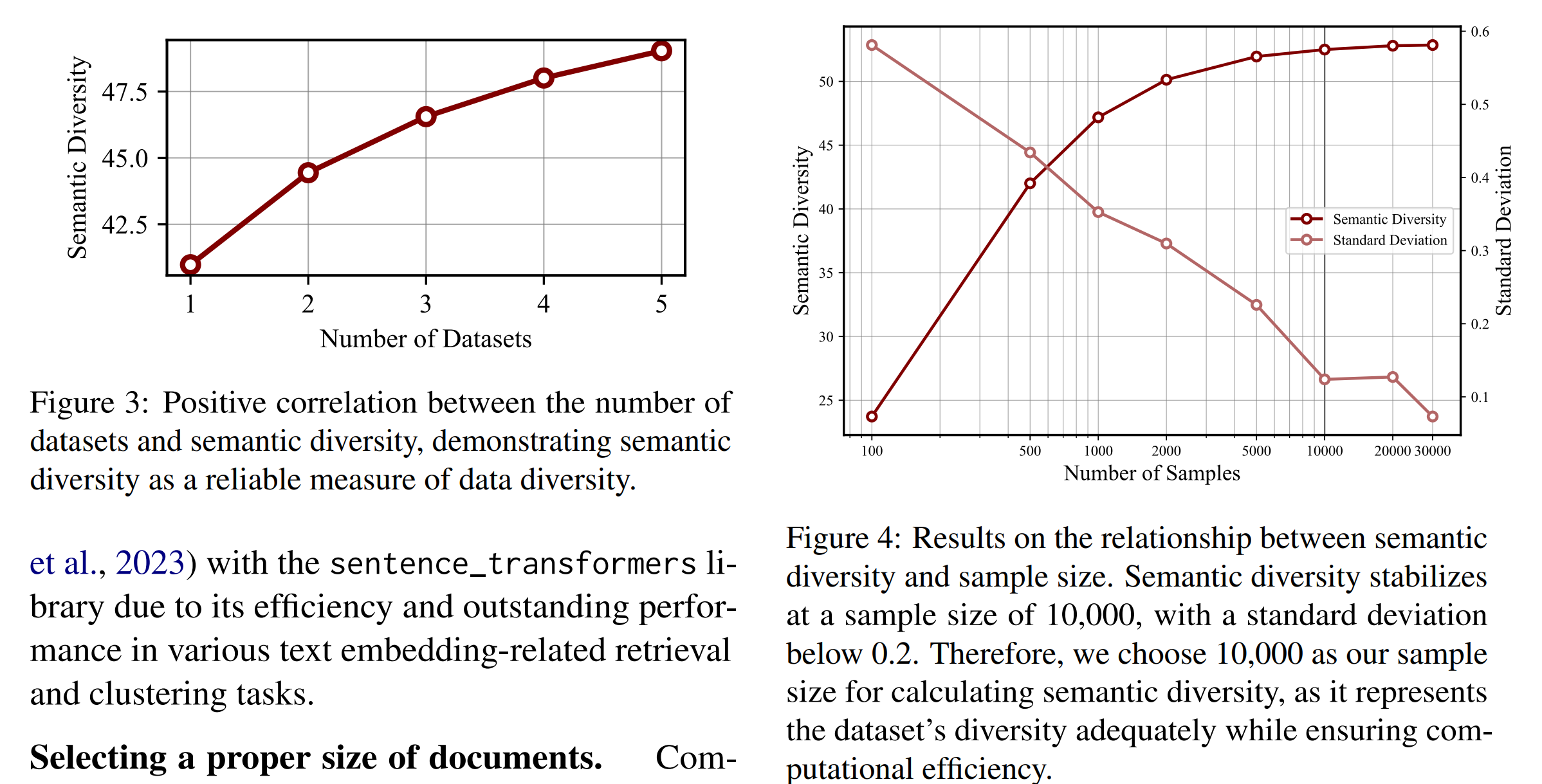
계산 제약으로 인해 데이터셋의 모든 문서에 대해 의미론적 다양성을 계산할 수는 없습니다. 필터링되지 않은 데이터셋에 대한 실험은 의미론적 다양성 지표를 계산할 적절한 문서 수를 선택하는 데 도움을 줍니다. 각 실험에서 무작위로 $n$ 샘플을 선택하여 의미론적 다양성 점수를 계산하고, 이 과정을 10회 반복하여 평균 점수와 표준 편차를 계산했습니다. 실험 결과, 샘플 크기가 10,000을 초과할 때 의미론적 다양성이 안정화되었으며, 표준 편차는 0.12로 나타났습니다. 따라서, 계산 효율성과 정확성을 균형 있게 유지하기 위해 후속 실험에서 샘플 크기 10,000을 선택했습니다.
데이터셋의 다양성을 반영하는 지표
실험은 의미론적 다양성이 다중 데이터셋 환경에서 데이터 다양성을 효과적으로 반영함을 보여줍니다. 다양한 주제나 글쓰기 스타일을 가진 다섯 가지 데이터셋(CC-News, IMDB, Reddit, Wikipedia, OpenWebText)에서 동일한 수의 샘플을 추출하여 혼합된 하위 집합을 구성한 후, 의미론적 다양성과 데이터셋 수(N) 간의 관계를 분석했습니다. 결과는 의미론적 다양성이 데이터셋 수(N)와 긍정적인 상관관계를 가지며, 데이터셋 내의 다양성을 정확하게 반영함을 보여줍니다.
품질 필터링이 다양성에 미치는 영향
다양한 품질 필터링 방법을 통해 얻은 데이터셋의 의미론적 다양성을 평가했습니다. 대부분의 품질 필터는 원시 데이터셋보다 더 높은 다양성을 유지했으며, 이는 유사한 의미를 가진 기계 생성 스팸 문서를 대량으로 제거한 결과일 수 있습니다. 중요도 재표집은 가장 높은 다양성을 기록했으며, 이는 재표집 전략의 결과로 보입니다. ScalingFilter는 참조 데이터를 사용하지 않기 때문에, 가장 일반적으로 사용되는 이진 분류보다 더 큰 다양성을 나타냈습니다.
Perplexity 게이팅은 원시 데이터셋의 다양성을 감소시켰으며, 이는 Perplexity 임계값에 따라 데이터를 필터링하는 것이 데이터 다양성에 예기치 않은 편향을 초래할 수 있음을 뒷받침합니다.
필터링 전처리에 따른 다양성 감소 색인마킹
이와 같은 실험 결과와 분석을 통해 ScalingFilter는 다양한 downstream 작업에서 향상된 성능을 발휘하며, 데이터셋의 다양성을 효과적으로 보존함을 확인할 수 있습니다.
4. 관련 연구 (Related Work)
- 품질 필터링 연구: 다양한 데이터 품질 필터링 접근 방식과 그 한계에 대해 논의
- 스케일링 법칙 연구: 모델 크기, 데이터셋 크기, 계산 예산, 성능 간의 관계를 정량화하는 스케일링 법칙의 발전과 연구
- ScalingFilter의 성과와 한계를 요약하고, 향후 연구 방향을 제안
품질 필터링 (Quality Filtering)
대규모 언어모델(LLM)의 pre-training dataset에는 유해한 기계 생성 스팸이나 비정상적인 형식과 같은 저품질 콘텐츠가 완전히 제거되지 않았을 가능성이 높습니다. 이런 데이터를 필터링하기 위해 연구자들은 일반적으로 선형 분류기나 언어 모델을 사용하여 문서에 점수를 매기고, 이 점수에 기반해 데이터를 필터링합니다. 고품질 데이터의 대표적인 예로는 Wikipedia, 책, OpenWebText 등이 있으며, 초기 연구들(Brown et al., 2020; Chowdhery et al., 2023)은 이런 데이터를 참조 데이터로 활용하여 필터링 방법을 개발했습니다.
예를 들어, 초기 연구에서는 이진 분류기를 사용해 큐레이션된 데이터셋을 필터링되지 않은 CommonCrawl 데이터와 비교하고, Pareto Randomness를 사용한 노이즈 임계치 설정을 통해 데이터 품질을 향상시키려고 했습니다. 그러나 데이터 품질을 저하시킬 수 있다는 지적(Xie et al., 2023)이 있었으므로, 최근 연구들(Touvron et al., 2023)에서는 Wikipedia를 유일한 양성 클래스로 설정하고 강력한 임계치를 적용했습니다. 하지만, 유일한 양성 클래스로 설정하고 강력한 임계치로 적용함에 따라 코퍼스의 다양성을 제한하고 편향을 도입할 가능성이 있습니다.
언어 모델을 사용하는 또 다른 접근 방식으로는 Wenzek et al. (2019)이 제안한 n-gram 모델이 있습니다. 이 모델은 Wikipedia에서 학습되어 Perplexity에 따라 문서를 head, middle, tail로 분류하고, 낮은 Perplexity 문서만을 사전 학습에 사용합니다. 하지만 Perplexity 기반 필터링은 예측하기 쉬운 텍스트를 선호하게 되어 도전적이지만 고품질인 콘텐츠를 폐기할 위험이 있습니다(Marion et al., 2023).
이에 반해, 접근 방식인 ScalingFilter는 두 개의 언어 모델을 활용해 품질 계수를 도출하여 이런 문제를 해결하려 합니다.
스케일링 법칙 (Scaling Laws)
스케일링 법칙은 모델 크기, 데이터셋 크기, 계산 예산, 성능 간의 관계를 정량화합니다. 초기 연구(Hestness et al., 2017; Kaplan et al., 2020)는 이런 요소들 간에 멱법칙 관계가 있음을 밝혔습니다. Hoffmann et al. (2022)은 데이터 종속적인 스케일링 항을 포함하는 통합된 스케일링 법칙 공식을 제시했습니다. 최근 연구들은 다중 언어(Conneau et al., 2019) 및 다중 모드(Henighan et al., 2020; Cherti et al., 2023) 환경에서의 스케일링 법칙 변동을 보여주었습니다. Aghajanyan et al. (2023)은 이런 주제를 면밀히 분석하여 단일 모달 및 혼합 모달 환경에서 다양한 스케일링 법칙 파라미터를 도출하며, 데이터 모달리티가 스케일링 행동에 미치는 영향을 강조했습니다.
이 발견은 데이터 품질의 변화가 스케일링 행동에 영향을 미친다는 가설을 시사합니다. 최근 연구(Bi et al., 2024)는 데이터 품질이 스케일링 법칙에서 모델 및 데이터 스케일링 지수에 영향을 미친다는 것을 확인했습니다. 이 연구는 스케일링 법칙 파라미터와 데이터 품질 간의 연결고리를 입증하며, 스케일링 속성을 기반으로 고품질 샘플을 선택할 수 있게 합니다.
5. 결론 (Conclusion)
본 연구에서는 참조 데이터에 의존하지 않는 데이터 품질 필터링 방법인 ScalingFilter를 제안했습니다. 스케일링 법칙에서 출발하여, 서로 다른 크기의 언어 모델(즉, 메타 모델) 간의 Perplexity 차이가 데이터 품질과 긍정적으로 상관관계가 있음을 입증했습니다. Perplexity 차이(즉, 품질 계수)가 높은 샘플을 선택하여 pre-training dataset셋을 구성했습니다. 참조 데이터셋으로 인한 편향을 제거함으로써, 방법은 데이터 다양성을 유지하면서도 여러 강력한 베이스 라인보다 더 나은 downstream 성능을 달성했습니다.
한계 (Limitations)
ScalingFilter에는 해결해야 할 몇 가지 한계가 있습니다. 첫째, 두 LLM 간의 Perplexity 차이에 의존하므로 사실적 정확성이나 인종 편향, 사회 계층 편향, 성별 편향과 같은 텍스트 품질의 미묘한 측면을 놓칠 수 있습니다. 둘째, 대규모 데이터셋의 Perplexity 차이를 계산하려면 상당한 계산 자원이 필요합니다. 셋째, 다른 언어 및 데이터가 제한된 도메인에 적용 가능할지에 대한 불확실성이 있습니다. 향후 연구에서는 이런 한계를 해결하고, 의미론적 다양성과 모델 성능 간의 관계, 특히 공정성과 편향과 관련된 부분을 더욱 탐구해야 할 것입니다.
[참고자료 1] Pareto Randomness
Pareto 분포는 ‘80-20 법칙’으로도 알려진 현상을 설명하는 확률 분포입니다. 이 분포는 많은 자연적, 사회적 현상에서 관찰되며, 소수의 원인이 결과의 대부분을 차지하는 불균형한 관계를 나타내는 데 사용됩니다.
Pareto Randomness는 Pareto 분포의 특성을 활용한 임의성을 의미하며, 주로 다음과 같은 맥락에서 사용됩니다.
- 데이터 필터링: 높은 품질의 데이터를 선별하는 과정에서 사용
- 노이즈 임계값 설정: 데이터셋에서 노이즈를 제거하기 위한 임계값을 결정할 때 활용
- 샘플링 기법: 불균형한 분포를 가진 데이터에서 샘플을 추출할 때 사용 가능
- 최적화 알고리즘: 특정 최적화 문제에서 탐색 공간을 효율적으로 탐색하는 데 활용될 수 있음
Pareto Randomness는 Pareto 분포의 “long tail” 특성을 활용하여, 드물지만 중요한 사건이나 데이터 포인트를 포착하는 데 유용할 수 있지만, 이 방법을 사용할 때는 데이터의 대표성과 다양성을 해칠 수 있으므로 추가적인 검증이 필요합니다.
Pareto 분포의 확률 밀도 함수(PDF)
\[f(x) = \frac{\alpha x_m^\alpha}{x^{\alpha+1}}, \quad x \geq x_m\]$x$는 관심 변수 $x_m$은 최소값 (스케일 파라미터) $\alpha$는 형태 파라미터 ($\alpha > 0$)
Pareto Randomness를 데이터 필터링에 적용 단계
- 데이터 품질 점수 계산: 각 데이터 포인트에 대해 품질 점수를 계산
- Pareto 분포 피팅: 품질 점수에 Pareto 분포를 피팅
- 임계값 설정: Pareto 분포의 특정 백분위수를 임계값으로 설정
- 데이터 필터링: 임계값 이상의 품질 점수를 가진 데이터만 선택
Pareto Randomness를 사용한 데이터 필터링 과정 (예시 코드)
- Pareto 분포를 따르는 데이터 품질 점수를 생성
- 실제 데이터에 Pareto 분포를 피팅
- 80번째 백분위수를 임계값으로 설정
- 임계값 이상의 데이터만 필터링하여 선택
- 원본 데이터와 필터링된 데이터의 분포를 시각화
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# 데이터 생성
np.random.seed(42)
data_quality = np.random.pareto(2, 10000) + 1 # 형태 파라미터 α=2, 최소값 x_m=1
# Pareto 분포 피팅
shape, loc, scale = stats.pareto.fit(data_quality)
# 임계값 설정 (e.g., 80번째 백분위수)
threshold = np.percentile(data_quality, 80)
# 데이터 필터링
filtered_data = data_quality[data_quality >= threshold]
# 시각화
plt.figure(figsize=(10, 6))
plt.hist(data_quality, bins=50, density=True, alpha=0.7, label='Original Data')
plt.hist(filtered_data, bins=50, density=True, alpha=0.7, label='Filtered Data')
x = np.linspace(min(data_quality), max(data_quality), 100)
plt.plot(x, stats.pareto.pdf(x, shape, loc, scale), 'r-', lw=2, label='Fitted Pareto PDF')
plt.axvline(threshold, color='g', linestyle='--', label='Threshold')
plt.xlabel('Data Quality Score')
plt.ylabel('Density')
plt.title('Pareto Randomness in Data Filtering')
plt.legend()
plt.show()
print(f"Original data size: {len(data_quality)}")
print(f"Filtered data size: {len(filtered_data)}")
print(f"Percentage of data retained: {len(filtered_data) / len(data_quality) * 100:.2f}%")
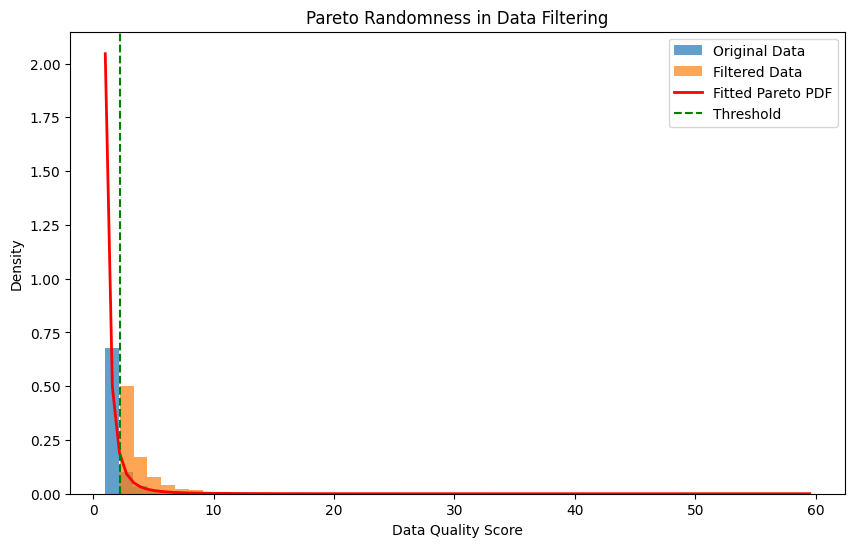
이 방법의 장점은 데이터의 자연스러운 분포를 고려하면서 품질이 높은 데이터를 선별할 수 있다는 거지만, Xie et al. (2023)이 지적한 대로, 이 방법이 데이터의 다양성을 제한하거나 특정 유형의 데이터를 과도하게 제거할 수 있다는 단점을 갖고 있습니다.
Pareto 임의성을 사용할 때는 임계값 설정, 필터링 후 데이터의 대표성, 그리고 가능한 편향 등을 신중히 고려해야 하며, 다양한 평가 지표를 사용하여 필터링된 데이터셋의 품질과 다양성을 확인해야 합니다.