POST | Estimation FLOPs of LLaMA-2

• Related Project: Private
• Category: Post
• Author: Minwoo Park
• Date:2023-05-26

비공개 포스트 초안

Contents

• Transformers
  • FLOPs of Transformers
    • FLOPs of LLaMA-2 7B Model
  • Transformer Model Computation Details
    • Self-Attention Layer Calculations
      • Step 1: Calculating Attention Score
      • Step 2: Estimating Total FLOPs
      • Step 3: Feed-Forward Network (FFN) layers:
    • Total FLOPs Calculations
  • Rough Estimation of Arithmetic Intensity
• 트랜스포머
  • 트랜스포머의 FLOPs
    • LaMA-2 7B 모델의 FLOPs 추산
  • VRAM 요구량 추산
  • Arithmetic Intensity 추산
• References

In this post…

• We examine formulas for calculating FLOPs required for training and inference of Transformers while maintaining the format.
• Based on the calculated results, we compute the FLOPs of the standard LLaMA-2 7B architecture and attempt to simplify the formulas for easier estimation.

Target Audience: Developers
Estimated Reading Time: 15 minutes

This post references Hugging Face’s post: Methods and tools for efficient training on a single GPU, and for more detailed information, please refer to Stas Bekman’s Machine Learning Engineering. Other images and materials referenced are duly credited.

Transformers

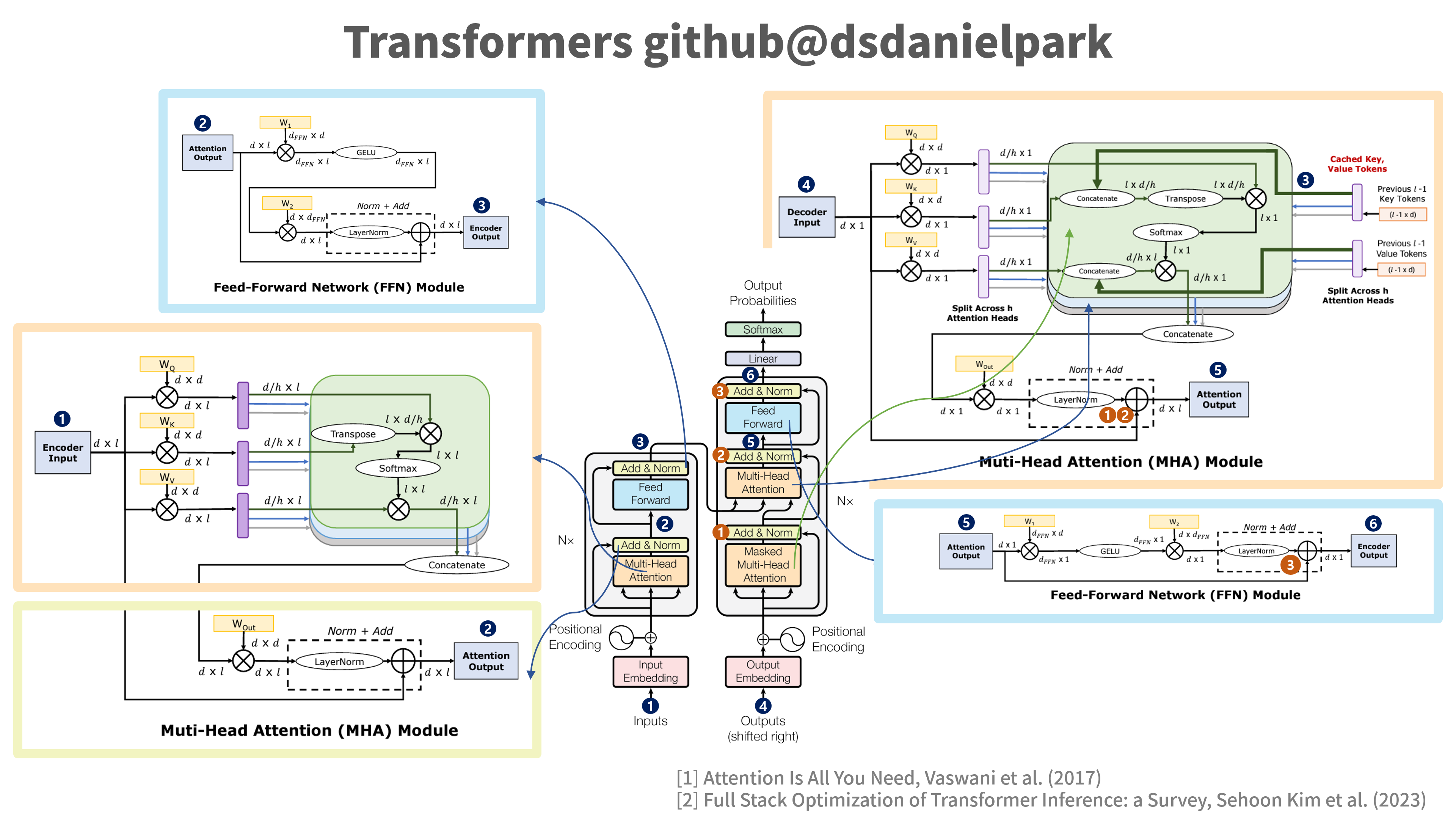
*Figure 1: The image is reconstructed by the author based on Attention Is All You Need (Vaswani et al., 2017) and Full Stack Optimization of Transformer Inference: a Survey (Sehoon kim et al. 2023).

FLOPs of Transformers

Let’s estimate the FLOPs (Floating Point Operations) of Transformers models.

We’ll examine the parameters influencing Transformers’ FLOPs. Attention layers and Feed-Forward Network (FFN) layers predominantly contribute to the FLOPs, while layer normalization and residual connections have relatively less impact on the total FLOPs. Therefore, we can primarily estimate based on attention layers and FFN layers.

Before estimating FLOPs, let’s summarize the necessary parameters:

• Sequence Length: Maximum number of input tokens the model can handle.
• Hidden Units: Number of hidden units in each layer.
• Layers: Total number of layers in the Transformer model.
• Heads: Number of heads in multi-head attention.
• FFN Inner Dimension: Dimensionality within the FFN (Feed-Forward Network) layer.

Attention layers and FFN layers predominantly contribute to the total FLOPs. Let’s derive the formula for calculating total FLOPs and examine it slowly as depicted in the figure:

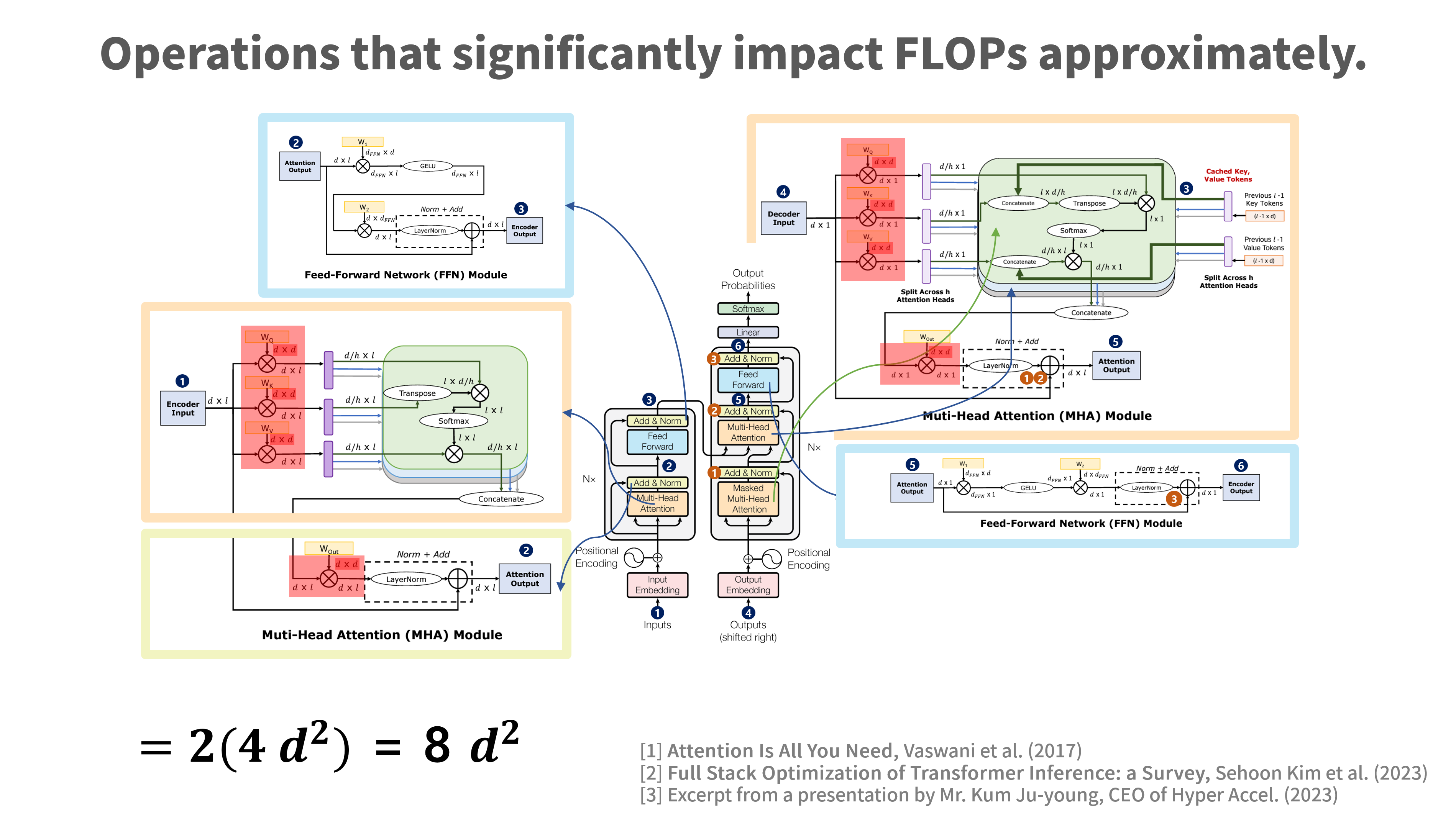
Figure 2: The image is reconstructed by the author based on Attention Is All You Need (Vaswani et al., 2017), Full Stack Optimization of Transformer Inference: a Survey (Sehoon kim et al. 2023), and presentation materials by Kim Jooyoung, CEO of Hyper Accel.

FLOPs of LLaMA-2 7B Model

Let’s estimate the FLOPs of the LLaMA-2 7B model, considering the specific architecture information.

We’ll ignore the model’s layer normalization and residual connections and focus on the FLOPs of attention layers and FFN layers.

The architecture used for estimation of the LLaMA-2 7B model is as follows:

  from transformers import AutoTokenizer
  import transformers
  import torch

  model = "meta-llama/Llama-2-7b-hf"

  tokenizer = AutoTokenizer.from_pretrained(model)
  pipeline = transformers.pipeline(
      "text-generation",
      model=model,
      torch_dtype=torch.float16,
      device_map="auto",
  )

  sequences = pipeline(
      'I liked "Breaking Bad" and "Band of Brothers". Do you have any recommendations of other shows I might like?\n',
      do_sample=True,
      top_k=10,
      num_return_sequences=1,
      eos_token_id=tokenizer.eos_token_id,
      max_length=200,
  )
  for seq in sequences:
      print(f"Result: {seq['generated_text']}")
  

  print(pipeline.model.config)
  

  LlamaConfig {
    "_name_or_path": "meta-llama/Llama-2-7b-hf",
    "architectures": [
      "LlamaForCausalLM"
    ],
    "bos_token_id": 1,
    "eos_token_id": 2,
    "hidden_act": "silu",
    "hidden_size": 4096,
    "initializer_range": 0.02,
    "intermediate_size": 11008,
    "max_position_embeddings": 4096,
    "model_type": "llama",
    "num_attention_heads": 32,
    "num_hidden_layers": 32,
    "num_key_value_heads": 32,
    "pad_token_id": 0,
    "pretraining_tp": 1,
    "rms_norm_eps": 1e-05,
    "rope_scaling": null,
    "tie_word_embeddings": false,
    "torch_dtype": "float16",
    "transformers_version": "4.31.0",
    "use_cache": true,
    "vocab_size": 32000
  }
  

  print(pipeline.model)
  

LlamaForCausalLM(
  (model): LlamaModel(
    (embed_tokens): Embedding(32000, 4096, padding_idx=0)
    (layers): ModuleList(
      (0-31): 32 x LlamaDecoderlayer(
        (self_attn): Llamaattention(
          (q_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (k_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (v_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (o_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (rotary_emb): LlamaRotaryEmbedding()
        )
        (mlp): LlamaMLP(
          (gate_proj): Linear(in_features=4096, out_features=11008, bias=False)
          (up_proj): Linear(in_features=4096, out_features=11008, bias=False)
          (down_proj): Linear(in_features=11008, out_features=4096, bias=False)
          (act_fn): SiLUActivation()
        )
        (input_layernorm): LlamaRMSNorm()
        (post_attention_layernorm): LlamaRMSNorm()
      )
    )
    (norm): LlamaRMSNorm()
  )
  (lm_head): Linear(in_features=4096, out_features=32000, bias=False)
)
  

In order to make estimations, let’s summarize the necessary parameter values:

• Sequence Length: 512
  • We assume a sequence length of 512. (For LLaMA2, it can be set up to 4,096.)
• Hidden Units: 4,096
• Number of Layers: 32
• Heads: 32
• FFN Inner Dimension (Intermediate Size): 11,008
  • The number of heads should be a divisor of 4,096. The LLaMA-2 7B model is set to 32 heads. Each head performs attention over different parts of the input sequence, enabling the model to process information in parallel while sharing diverse information. To evenly share information while parallelizing, the number of hidden units should be divisible by the number of heads. Adjustments can be made to avoid bottlenecks according to resource constraints.

Transformer Model Computation Details

Self-Attention Layer Calculations

• Each self-attention layer in the Transformers model performs matrix multiplication for queries, keys, and values.
  • Query, Key, Value Matrix Creation: The input matrix (Embedded Token Matrix) is transformed into Query $(Q)$, Key $(K)$, and Value $(V)$ matrices. This involves matrix multiplication between each input matrix and its corresponding weight matrix $(W_Q, W_K, W_V)$, and this process is performed independently for each head.
  • Consequently, since we need to multiply the dot product of queries and keys by the value matrix, we multiply by 2 in the equation below.

Step 1: Calculating Attention Score

• Attention scores are computed through the dot product between the transpose of $Q$ and $K$, and $V$ is multiplied by the attention score to generate the final output.
  • The self-attention calculation includes dot products for Query, Key, and Value matrices, each of size $2 \times (\text{Sequence Length} \times \text{Hidden Units} \times \text{Hidden Units})$ for one self-attention layer.

Step 2: Estimating Total FLOPs

• By multiplying the FLOPs of self-attention calculated above by the number of layers, we can estimate the total FLOPs of all attention layers executed in a single head, as follows:
  • $(\text{Self-Attention FLOPs / Head}) = 2 \times (\text{Sequence Length}) \times (\text{Hidden Dimension})^2$
• Transformers employ multi-head attention, so by multiplying the $(\text{self-attention FLOPs / Head})$ obtained above by the total number of heads, we can calculate the FLOPs for all attention layers.

• Calculation for LLaMA-2 7B
  • $(\text{Self-attention FLOPs / Head}) = 2 \times 512 \times 4096^2$
  • $\text{Total Attention Layers FLOPs} = (\text{Self-attention FLOPs / Head}) \times (\text{Heads} \times \text{Layers})$
  • $\text{Total Attention Layers FLOPs} = 2 \times 512 \times 4096^2 \times 32 \times 32$
  • $\text{Total Attention Layers FLOPs} = 4,294,967,296 \text{ FLOPs}$

Step 3: Feed-Forward Network (FFN) layers:

• FFN typically includes two linear layers.
  • Considering two linear transformations within FFN (from input dimension to intermediate dimension, and from intermediate dimension to output dimension), but since FFN operates independently at each layer, we only need to multiply by the number of layers for FFN.
• $(\text{FLOPs / FFN}) = 2 \times (\text{Sequence Length}) \times (\text{Hidden Dimension}) \times (\text{FFN Dimension}) \times 2$
• By multiplying the above equation by the number of layers, we can estimate the total FLOPs of all FFN layers, as follows:

• Calculation for LLaMA-2 7B
  • $(\text{FFN Layer FLOPs}) = 2 \times 2 \times 512 \times 4096 \times 11008$
  • $\text{Total FFN Layers FLOPs} = (\text{FFN Layer FLOPs}) \times 32 \text{ Layers}$

Total FLOPs Calculations

• Ignoring other components’ FLOPs, we can approximate the FLOPs of transformers by adding equations (1) and (2). (FLOPs for Other Components can be disregarded compared to self-attention and FFN)

• Calculation for LLaMA-2 7B:

  \[\begin{aligned} \text{Total FLOPs} = & (\text{Total FLOPs for attention Layers}) \\ & + (\text{Total FLOPs for FFN Layers}) \end{aligned}\] \[\begin{aligned} \text{Total FLOPs} = & 32 \text{ Layers} \times [(2 \times (512)^2 \times (4,096)^2 \\ & + 4 \times 512 \times 4,096 \times 11,008) \\ & \times 32 \text{ Heads}] \end{aligned}\]

  $= 20,547,123,544,064 \quad … \text{(Value 1)}$

The above content can be summarized into Python code as follows:

# Given parameters
sequence_length = 512
hidden_units = 4096
number_of_layers = 32
heads = 32
ffn_inner_dim = 11008

# Calculating FLOPs
# 1. FLOPs for Self-Attention layers per layer
flops_per_attention_layer = 2 * sequence_length * hidden_units * hidden_units

# Total FLOPs for all Self-Attention layers
total_flops_attention = flops_per_attention_layer * number_of_layers * heads

# 2. FLOPs for Feed-Forward Network (FFN) layers per layer
flops_per_ffn_layer = 2 * 2 * sequence_length * hidden_units * ffn_inner_dim

# Total FLOPs for all FFN layers
total_flops_ffn = flops_per_ffn_layer * number_of_layers

# 3. Total FLOPs
total_flops = total_flops_attention + total_flops_ffn
total_flops

The Total FLOPs for the LLaMA-2 7B model with a sequence length of 512 is 20,547,123,544,064, excluding calculations for layer normalization, residual connections, etc.

For inferring a single token, the required sequence is obtained by dividing this by 512, resulting in a value of 40,131,100,672.

Conclusively, the FLOPs for the LLaMA-2 model can be computed using the following expression:

Simplified, this can be expressed as: \(\begin{aligned} \text{Total FLOPs} \approx \text{Number of Layers} \times [ & (2 \times (\text{Sequence Length})^2 \times (\text{Hidden Units})^2 \\ & + 4 \times \text{Sequence Length} \times \text{Hidden Units} \\ & \quad \times \text{FFN Inner Dimension}) \\ & \times \text{Number of Heads} ] \end{aligned}\)

Substituting this into a simpler formula, we arrive at (Equation 4), resulting in a value of 2,199,023,255,552 for the LLaMA-2 7B model:

\(\text{Simplified Total FLOPs} = L^2 \times H^2 \times 4D \times \text{Heads} \times \text{Layers} \quad \text{... (Equation 4)}\) \(= (32^2) \times (4096^2) \times (4 \times 11008) \times 32 \times 32\) \(= 2,199,023,255,552 \quad \text{... (Value 3)}\)

• $L$: Sequence Length
• $H$: Hidden Units
• $Layers$: Number of Layers
• $D$: FFN Inner Dimension
• $Heads$: Number of Heads

The total FLOPs required for a sequence length of 512 in the LLaMA-2 7B model are 20,547,123,544,064. When this is divided by 512, the FLOPs required for a single token are calculated to be 40,131,100,672.

Assuming the prediction of a single token, we can substitute \(L = 1\) into the simplified expression, resulting in the following formula for per-token computation:

Given this simplification, the FLOPs per single token are computed as 4,294,967,296.

The estimated value from the comprehensive FLOP calculation (referred to previously as Equation 4) is 2,199,023,255,552. A discrepancy is observed between this value and the total FLOPs for the sequence (20,547,123,544,064), attributed to the exclusion of calculations for components such as layer normalization and residual connections, focusing instead solely on the sequence length of 512.

Thus, the FLOPs for one token can be determined to be either 40,131,100,672 or 4,294,967,296, depending on the level of simplification and the components included in the calculation.

Conclusively, for the standard architecture of the LLaMA-2 7B model, an approximate total FLOPs calculation for a single token prediction can be represented by scaling up the simplified estimation by a factor of ten:

In the context where the usage of MoE (Mixture of Experts) layers in GPT-4 is becoming established, open-source models like Mistral have also introduced services utilizing MoE. In such scenarios, assuming Mistral 7B utilizes at least two of its eight expert models for inference, the system may either repetitively load models into memory or keep all eight 7B models in VRAM, necessitating repeated VRAM loading and unloading (I/O).

When considering the usage of multiple expert models, the linear demand for VRAM specifications increases. For instance, assuming all eight LLMs are LLaMA-2 7B models, naive inference with all parameters stored in 32 bits would require 4 bytes per parameter * 70 billion parameters = 280 billion bytes × 8 = 224 GB of VRAM. Even with inference using 16 bits (2 bytes) per parameter, it would require 112 GB of VRAM. This is for the case of a 7B model; however, if larger parameter LLMs such as 13B, 70B, or 180B were to be used (though it’s rare to deploy such large models in multiple quantities due to the nature of MoE), the VRAM specification required would increase geometrically.

The A100 GPU is designed with a default of 40 GB of VRAM, and even with an 80 GB A100, inference tasks could become challenging.

In terms of precision (float32), all model parameters are stored as 32 bits (or 4 bytes). Hence, for inference, 4 bytes per parameter * 70 billion parameters = 280 billion bytes = 28 GB of GPU memory would be required. For half precision, where each parameter is stored as 16 bits (or 2 bytes), only 14 GB would be required for inference. In the case of using 8-bit and 4-bit algorithms, each parameter would use 4 bits (or 1/2 byte), requiring 3.5 GB of memory for inference.

For training, the memory requirement per parameter typically doubles due to the storage of gradients and second-order gradients when using standard AdamW. Therefore, for a 7B model, during training, 8 bytes per parameter * 70 billion parameters = 56 GB of GPU memory would be required, multiplied by the number of expert models when adopting MoE.

Using AdaFactor reduces the memory requirement to 4 bytes per parameter, necessitating a total of 28 GB of GPU memory, while optimization programs for bits and bytes (e.g., 8-bit AdamW) would require 2 bytes per parameter, totaling 14 GB of GPU memory.

For further details, refer to the Hugging Face [Post: Methods and tools for efficient training on a single GPU].

Rough Estimation of Arithmetic Intensity

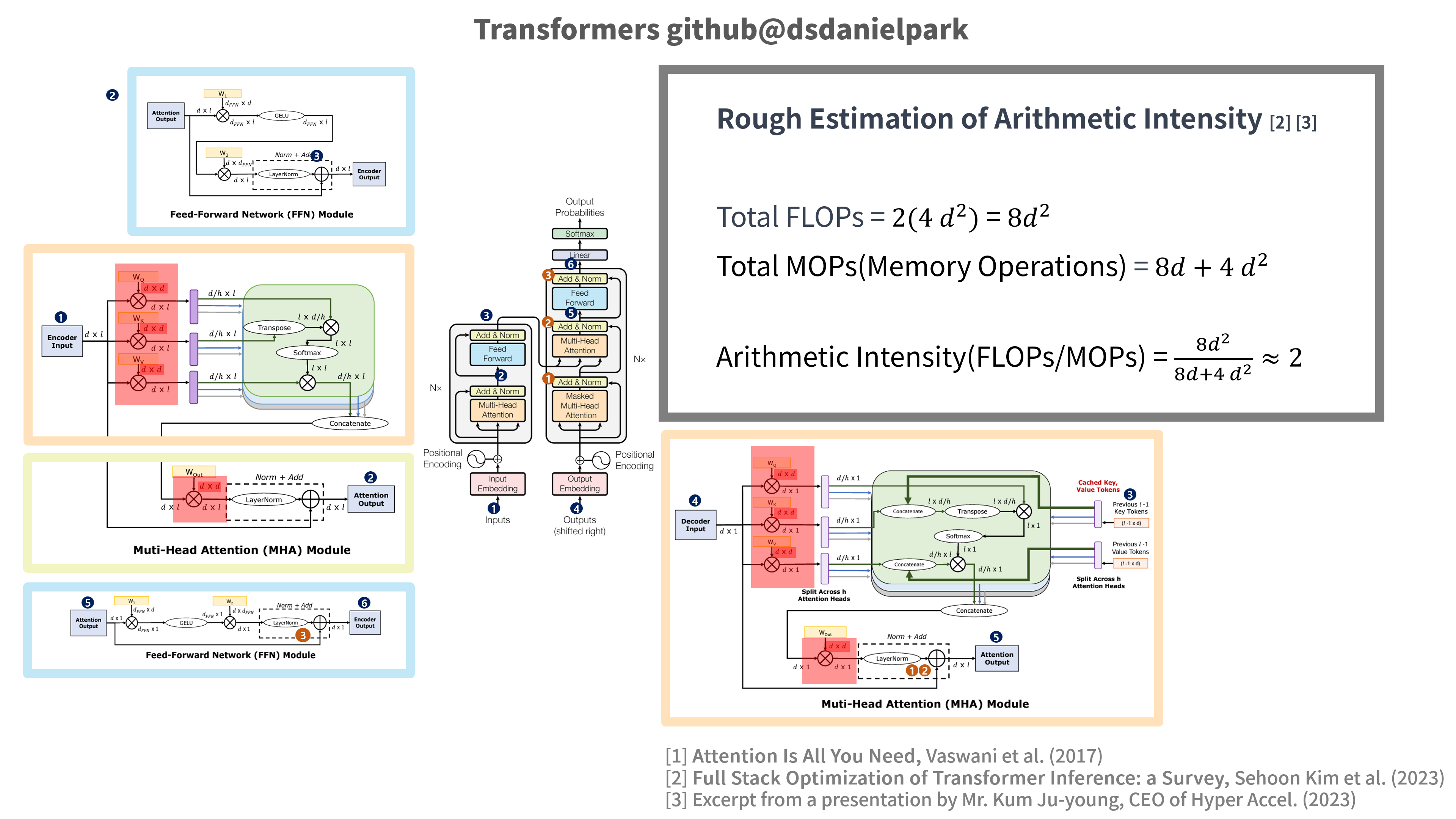
Figure 3: The image is reconstructed by the author based on Attention Is All You Need (Vaswani et al., 2017), Full Stack Optimization of Transformer Inference: a Survey (Sehoon Kim et al., 2023), and presentation materials from CEO Kim Jooyoung of Hyper Accel.

이 포스트에서는 …

• Transformers의 학습과 인퍼런스에 필요한 FLOPs를 계산할 수 있는 식에 대해서 살펴봅니다.
• 계산 결과를 바탕으로 표준 LLaMA-2 7B 아키텍처의 FLOPs를 계산하고, 더 간단하게 추산할 수 있도록 식을 변형해봅니다.

본 포스트는 허깅 페이스의 포스트: Methods and tools for efficient training on a single GPU을 참고하였으며, 더 자세한 내용은 Stas Bekman의 Machine Learning Engineering을 참고하세요. 그 외 참조한 이미지 등은 출처를 표기하여두었습니다.

트랜스포머

*Figure 1: 이미지는 Attention Is All You Need (Vaswani et al., 2017) 및 Full Stack Optimization of Transformer Inference: a Survey (Sehoon kim et al. 2023)을 기반으로 필자가 재구성하였습니다.

트랜스포머의 FLOPs

Transformers 모델의 FLOPs(Floating Point Operations)를 추산해보겠습니다.

Transformers FLOPs에 영향을 주는 파라미터들을 살펴보겠습니다. attention layers 및 FFN(Feed-Forward Network) layers가 FLOPs의 대부분을 차지하며, layer normalization, residual connections은 상대적으로 total FLOPs에 영향을 덜 미치기 때문에, attention layers과 FFN layers 위주로 추산할 수 있습니다.

FLOPs를 추정하기에 앞서 필요한 파라미터를 정리하면 다음과 같습니다.

• 시퀀스 길이 (Sequence Length): 모델이 처리할 수 있는 최대 입력 토큰 수
• 히든 유닛 수 (Hidden Units): 각 레이어에서의 히든 유닛의 수
• 레이어 수 (layers): Transformer 모델에서 레이어의 총 수
• 헤드 수 (Heads): 멀티 헤드 어텐션에서의 헤드 수
• FFN 내부 차원(FFN Inner Dimension): FFN(Feed-Forward Network) 레이어에서의 내부 차원 수

Attention layer와 FFN layer의 FLOPs위주로 total FLOPs를 구하는 식을 구해보면, 다음과 같으며 Figure과 같이 천천히 살펴보겠습니다.

*Figure 2: 이미지는 Attention Is All You Need (Vaswani et al., 2017), Full Stack Optimization of Transformer Inference: a Survey (Sehoon kim et al. 2023) 그리고 Hyper Accel의 자료 등을 기반으로 재구성

LaMA-2 7B 모델의 FLOPs 추산

구체적인 아키텍처에 대한 정보가 있는 LLaMA-2 7B 모델의 FLOPs를 추산해보겠습니다. (모델의 layer normalization과 residual connections는 무시하고, attention layers와 FFN layers의 FLOPs 위주로 살펴봅니다.)

추산에 사용된 LLaMA-2 7B 모델의 아키텍처는 다음과 같으며,

  from transformers import AutoTokenizer
  import transformers
  import torch

  model = "meta-llama/Llama-2-7b-hf"

  tokenizer = AutoTokenizer.from_pretrained(model)
  pipeline = transformers.pipeline(
      "text-generation",
      model=model,
      torch_dtype=torch.float16,
      device_map="auto",
  )

  sequences = pipeline(
      'I liked "Breaking Bad" and "Band of Brothers". Do you have any recommendations of other shows I might like?\n',
      do_sample=True,
      top_k=10,
      num_return_sequences=1,
      eos_token_id=tokenizer.eos_token_id,
      max_length=200,
  )
  for seq in sequences:
      print(f"Result: {seq['generated_text']}")
  

  print(pipeline.model.config)
  

  LlamaConfig {
    "_name_or_path": "meta-llama/Llama-2-7b-hf",
    "architectures": [
      "LlamaForCausalLM"
    ],
    "bos_token_id": 1,
    "eos_token_id": 2,
    "hidden_act": "silu",
    "hidden_size": 4096,
    "initializer_range": 0.02,
    "intermediate_size": 11008,
    "max_position_embeddings": 4096,
    "model_type": "llama",
    "num_attention_heads": 32,
    "num_hidden_layers": 32,
    "num_key_value_heads": 32,
    "pad_token_id": 0,
    "pretraining_tp": 1,
    "rms_norm_eps": 1e-05,
    "rope_scaling": null,
    "tie_word_embeddings": false,
    "torch_dtype": "float16",
    "transformers_version": "4.31.0",
    "use_cache": true,
    "vocab_size": 32000
  }
  

  print(pipeline.model)
  

LlamaForCausalLM(
  (model): LlamaModel(
    (embed_tokens): Embedding(32000, 4096, padding_idx=0)
    (layers): ModuleList(
      (0-31): 32 x LlamaDecoderlayer(
        (self_attn): Llamaattention(
          (q_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (k_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (v_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (o_proj): Linear(in_features=4096, out_features=4096, bias=False)
          (rotary_emb): LlamaRotaryEmbedding()
        )
        (mlp): LlamaMLP(
          (gate_proj): Linear(in_features=4096, out_features=11008, bias=False)
          (up_proj): Linear(in_features=4096, out_features=11008, bias=False)
          (down_proj): Linear(in_features=11008, out_features=4096, bias=False)
          (act_fn): SiLUActivation()
        )
        (input_layernorm): LlamaRMSNorm()
        (post_attention_layernorm): LlamaRMSNorm()
      )
    )
    (norm): LlamaRMSNorm()
  )
  (lm_head): Linear(in_features=4096, out_features=32000, bias=False)
)
  

추산의 필요한 파라미터 값들을 정리하면 다음과 같습니다.

• 시퀀스 길이(Sequence Length): 512
  • 시퀀스 길이는 512로 가정합니다. (LLaMA2 경우 4,096까지 설정 가능)
• 히든 유닛 수 (Hidden Units): 4,096
• 레이어 수 (Number of layers): 32
• 헤드 수 (Heads): 32
• FFN 내부 차원(FFN Inner Dimension, Intermediate Size): 11,008
  • 헤드 수는 4096의 약수로 설정하면 됩니다. LLaMA-2 7B모델의 헤드 수는 32로 설정되어 있습니다. 각 헤드는 입력 시퀀스의 서로 다른 부분에 대해 어텐션을 수행하며, 모델이 다양한 정보를 공유하며 병렬적으로 처리하게 됩니다. 병렬 처리를 하며 균등한 정보를 서로 공유하기 위해 히든 유닛 수는 헤드 수로 나누어 떨어지게만 설정해주면 됩니다. 리소스 상황에 맞게 병목이 생기지 않게 조절해주면 됩니다.

1. Attention layers:
   • Transformers 모델의 각 self-attention layer는 queries, keys, values에 대한 행렬곱을 수행합니다.
     • 입력 행렬(Embedded Token Matrix)은 Query ($Q$), Key ($K$), Value ($V$) 행렬로 변환됩니다. 이는 각각 입력 행렬과 해당 가중치 행렬 $W_Q$, $W_K$, $W_V$ 사이의 행렬 곱을 수행하며, 이 과정은 각 헤드에 대해 독립적으로 수행됩니다.
     • Attention 점수는 $ Q $와 $ K $의 전치(transpose) 사이의 내적(dot product)을 통해 계산되며, 계산된 attention score에 $ V $를 곱해 최종 출력을 생성합니다.
     • 각 Self-attention 계산에는 Query, Key, Value 매트릭스에 대한 내적이 포함되며, 각각의 크기는 다음과 같습니다. \(2 \times (\text{Sequence Length} \times \text{Hidden Units} \times \text{Hidden Units})\)
   • Self-attention의 FLOPs는 레이어 수와 헤드 수를 곱하여 전체 attention layer의 FLOPs를 추정할 수 있습니다. \(\begin{aligned} (\text{Self-Attention FLOPs / Head}) = & 2 \times (\text{Sequence Length}) \times (\text{Hidden Dimension})^2 \end{aligned}\) \(\begin{aligned} \text{Total FLOPs for Self-Attention} = & [2 \times (\text{Sequence Length}) \times (\text{Hidden Dimension})^2] \\ & \times (\text{Number of Layers}) \times (\text{Number of Attention Heads}) \end{aligned}\)
2. Feed-Forward Network (FFN) layers:

   • FFN은 일반적으로 두 개의 선형 레이어를 포함하며, 이 레이어들은 입력 차원에서 중간 차원으로, 그리고 중간 차원에서 출력 차원으로의 두 개의 선형 변환을 수행합니다.

     \[\begin{aligned} (\text{FLOPs / FFN}) = & 2 \times (\text{Sequence Length}) \\ & \times (\text{Hidden Dimension}) \\ & \times (\text{FFN Dimension}) \times 2 \end{aligned}\] \[\begin{aligned} \text{Total FLOPs for FFN layers} = & [2 \times (\text{Sequence Length}) \\ & \times (\text{Hidden Dimension}) \\ & \times (\text{FFN Dimension}) \times 2] \\ & \times (\text{Number of Layers}) \end{aligned}\]
3. Total FLOPs:

   • 다른 components의 FLOPs를 무시하고, 계산된 self-attention과 FFN의 FLOPs를 더하여 전체 transformers 모델의 FLOPs를 추산할 수 있습니다.

     \[\begin{aligned} \text{Total FLOPs} = & (\text{Number of layers}) \\ & \times (\text{FLOPs for self-attention} \\ & \quad + \text{FLOPs for FFN}) \end{aligned}\]

위 내용을 파이썬 코드로 정리하면 다음과 같습니다.

# Given parameters (Llama-2)
sequence_length = 512
hidden_units = 4096
number_of_layers = 32
heads = 32
ffn_inner_dim = 11008

# Calculating FLOPs
# 1. FLOPs for Self-Attention layers per layer
flops_per_attention_layer = 2 * sequence_length * hidden_units * hidden_units

# Total FLOPs for all Self-Attention layers
total_flops_attention = flops_per_attention_layer * number_of_layers * heads

# 2. FLOPs for Feed-Forward Network (FFN) layers per layer
flops_per_ffn_layer = 2 * 2 * sequence_length * hidden_units * ffn_inner_dim

# Total FLOPs for all FFN layers
total_flops_ffn = flops_per_ffn_layer * number_of_layers

# 3. Total FLOPs
total_flops = total_flops_attention + total_flops_ffn
total_flops

512의 시퀀스 길이에 필요한 LLaMA-2 7B모델의 Total FLOPs는 20,547,123,544,064로, layer normalization, residual connections 등은 제외하고 계산하였습니다.

한 개의 토큰을 인퍼런스하는데 필요한 시퀀스는 이를 512로 나누면되므로 40,131,100,672라는 값을 얻을 수 있게 됩니다.

결론적으로 LLaMA-2 모델의 FLOPs는 다음과 같은 식을 통해 구할 수 있습니다.

더 간단히 정리하면 다음과 같으며:

이 수식을 LLaMA-2 7B 모델에 적용하면 다음과 같은 결과를 얻습니다.

• $L$ : Sequence Length
• $H$ : Hidden Units
• $D$ : FFN Inner Dimension

위 값은 512 시퀀스 길이에 필요한 총 FLOPs로 하나의 토큰에 필요한 FLOPs는 마찬가지로 512로 나누면 다음과 같은 식으로 4,294,967,296임을 알 수 있습니다.

(Simplified Total FLOPs / token) = 40,131,100,672 … (값 4)

# Given parameters
sequence_length = 512
hidden_units = 4096
number_of_layers = 32
heads = 32
ffn_inner_dim = 11008

# Calculate the simplified FLOPs
simplified_flops = number_of_layers**2 * hidden_units**2 * 4 * heads

simplified_flops

즉, 한 개의 토큰을 예측한다고 가정하면 \(L = 1\)로 대치할 수 있고, 다음과 같이 간단히 표현할 수 있습니다.

\(\text{(Simplified Total FLOPs / 1 Token)} = H^2 \times 4D \times \text{Heads} \times \text{Layers}\) \(\text{(Simplified Total FLOPs / 1 Token)} = 4,294,967,296\)

위 계산식의 추산 값은 2,199,023,255,552로, 영향이 미비한 component(layer normalization, residual connections)를 제외하고 계산한 값인 20,547,123,544,064와는 차이가 있지만 이는 512 길이의 시퀀스 길이에 따른 값입니다.

하나의 토큰에 대한 FLOPs 값은 40,131,100,672와 4,294,967,296으로 구할 수 있습니다.

결론적으로 LLaMA-2 7B의 표준 아키텍처에서는 추산식에 10배인 다음 식으로 전체 FLOPs를 추산할 수 있음을 알 수 있습니다.

• $L$ : Sequence Length
• $H$ : Hidden Units
• $D$ : FFN Inner Dimension

위와 같이 간단하게 근사하고, 다양한 요인들은 무시한다면 각 토큰 예측에 필요한 FLOPs의 대략적인 총량을 추정할 수 있습니다. 특히, 10배를 곱하는 과정은 대략적으로 직관적인 FLOPs를 구하기 위한 방법으로 부정확할 수 있습니다.

VRAM 요구량 추산

많은 사람들이 GPT-4가 MoE(Mixture of Experts, 이하 “MoE”) 레이어를 사용하는 것으로 추정하고 있는 상황에서, Mistral과 같은 오픈 소스 모델들도 MoE를 사용하는 서비스를 공개하였습니다. 이런 상황에서, Mistral 7B가 8개의 expert 모델 중 최소 2개 이상의 모델을 사용해 인퍼런스 한다고 가정할 경우, 메모리에는 반복적인 모델 로드를 수행하거나 혹은 8개의 7B 모델을 VRAM에 올려두어야하거나 반복적으로 VRAM에 올리고 내려야(I/O)할 수 있습니다.

위와 같이 복수개의 expert models를 사용한다고 가정할 경우, 선형적으로 요구하는 VRAM 메모리 사양이 늘어나게 되는데, 8개의 모든 LLM이 LLaMA-2 7B 모델이라고 가정하면, naive하게 모든 parameters가 32bits로 인퍼런스할 경우 4bytes/parameters * 70B parameters = 280억 bytes X 8 = 224GB의 VRAM을 요구하게 됩니다. 만약 16bits 또는 2bytes로 인퍼런스한다고 가정하여도, 112GB의 VRAM을 요구하고, 이는 단순히 7B 모델의 경우이므로 만약 13B, 70B, 180B 등 더 큰 파라미터의 LLM을 사용한다고 가정하면(MoE 특성상 이렇게까지 큰 모델들을 여러개 올리는 일이 거의 없겠지만), 기하 급수적으로 요구하는 VRAM 사양이 높아지게 됩니다.

A100이 기본적으로 40GB의 VRAM으로 설계되어 있고, 80GB A100으로도 인퍼런스가 힘들어질 수 있습니다.

전체 precision(float32)에서는 모델의 모든 parameters가 32bits(또는 4bytes)로 저장됩니다. 따라서 인퍼런스에만 4bytes/parameters * 70B parameters = 280억 bytes = 28GB의 GPU 메모리가 필요합니다. 절반의 precision에서는 각 parameters가 16bits(또는 2bytes)로 저장되므로 인퍼런스에만 14GB가 필요하고, 8bits 및 4bits 알고리즘의 경우 parameters당 각각 4bits(또는 1/2bytes)를 사용하는데 인퍼런스를 위해 3.5GB의 메모리가 필요합니다.

훈련의 경우 훈련하는 방식에 따라 다르지만, 일반적으로 일반 AdamW를 사용하는 경우 (parameters뿐만 아니라 해당 gradients 및 second-order gradients도 저장하므로) parameters당 8bytes가 필요합니다.

따라서, 7B 모델의 경우 학습시 parameters당 8bytes * 70억 개의 parameters = 56GB의 GPU 메모리가 필요하며, MoE를 채택할 경우 expert models의 수 만큼 곱해야 합니다.

AdaFactor를 사용하는 경우 parameters당 4bytes가 필요하고, 총 28GB의 GPU 메모리가 필요하며, bits와 bytes의 최적화 프로그램(e.g., 8bits AdamW)을 사용해도 parameters당 2bytes가 필요하여 총 14GB의 GPU 메모리를 확보해야 할 수 있습니다.

자세한 내용은 다음 허깅 페이스의 포스트: Methods and tools for efficient training on a single GPU를 참조하세요.

Arithmetic Intensity 추산

*Figure 3: 이미지는 Attention Is All You Need (Vaswani et al., 2017), Full Stack Optimization of Transformer Inference: a Survey (Sehoon kim et al. 2023) 그리고 Hyper Accel의 자료 등을 기반으로 재구성

References

[1] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin. “Attention Is All You Need.” arXiv preprint arXiv:1706.03762 (2017).
[2] Sehoon Kim, Coleman Hooper, Thanakul Wattanawong, Minwoo Kang, Ruohan Yan, Hasan Genc, Grace Dinh, Qijing Huang, Kurt Keutzer, Michael W. Mahoney, Yakun Sophia Shao, Amir Gholami. “Full Stack Optimization of Transformer Inference: a Survey” arXiv preprint arXiv:2302.14017 (2023).
[3] Decoding transformers on edge devices
[4] Hyper Accel

CC BY-NC-ND 4.0 KR. All right reserved.

Copyright (c) 2023 Author: Minwoo Park, South Korea
All Copyright (c) Reserved.