Legibility of LLM outputs
- Related Project: Private
- Category: Paper Review
- Date: 2024-07-18
Prover-Verifier Games improve legibility of LLM outputs
- url: https://arxiv.org/abs/2407.13692
- pdf: https://arxiv.org/pdf/2407.13692
- html: https://arxiv.org/html/2407.13692v1
- abstract: One way to increase confidence in the outputs of Large Language Models (LLMs) is to support them with reasoning that is clear and easy to check – a property we call legibility. We study legibility in the context of solving grade-school math problems and show that optimizing chain-of-thought solutions only for answer correctness can make them less legible. To mitigate the loss in legibility, we propose a training algorithm inspired by Prover-Verifier Game from Anil et al. (2021). Our algorithm iteratively trains small verifiers to predict solution correctness, “helpful” provers to produce correct solutions that the verifier accepts, and “sneaky” provers to produce incorrect solutions that fool the verifier. We find that the helpful prover’s accuracy and the verifier’s robustness to adversarial attacks increase over the course of training. Furthermore, we show that legibility training transfers to time-constrained humans tasked with verifying solution correctness. Over course of LLM training human accuracy increases when checking the helpful prover’s solutions, and decreases when checking the sneaky prover’s solutions. Hence, training for checkability by small verifiers is a plausible technique for increasing output legibility. Our results suggest legibility training against small verifiers as a practical avenue for increasing legibility of large LLMs to humans, and thus could help with alignment of superhuman models.
[GAN, 적대적 네트워크와 비슷한 컨셉]
Contents
TL;DR
- 대규모 언어모델의 출력을 휴먼이 이해하기 쉽게 만드는 훈련 방법을 제안
- 검증자(Prover)와 증명자(Verifier) 간의 게임을 통한 점진적 훈련으로 문제 해결
- 검증 가능성을 높이기 위해 반복 알고리즘을 통해 효과 검증
1. 서론
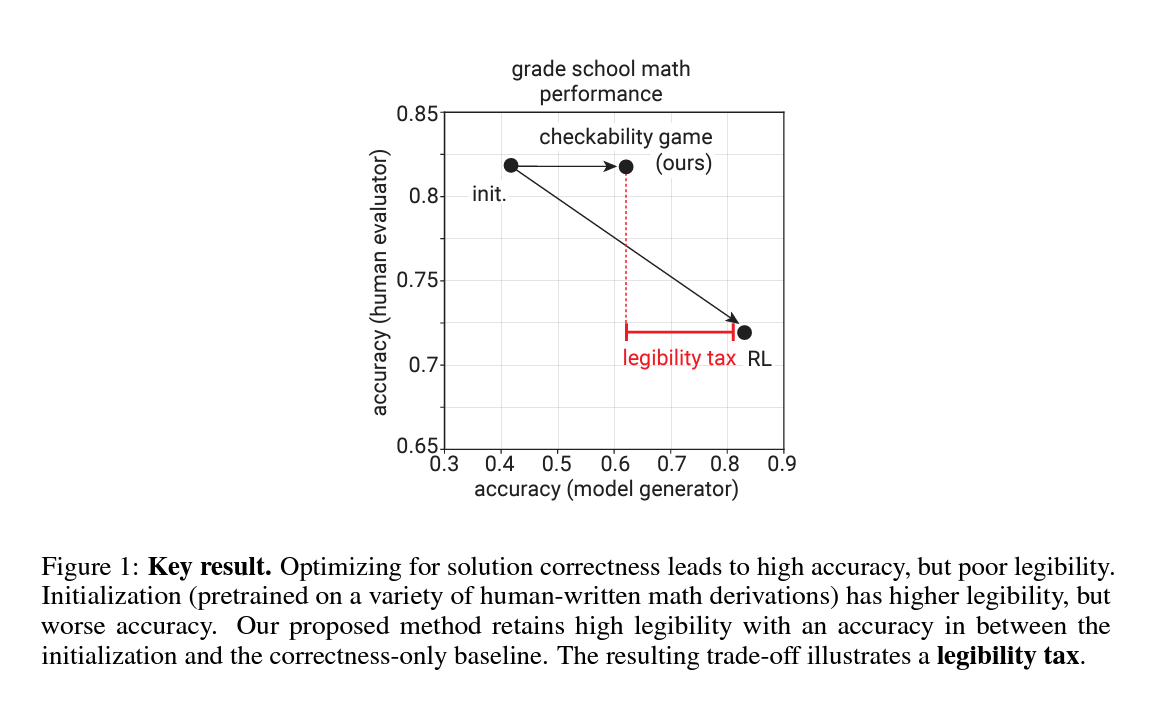
대규모 언어모델(Large Language Models, LLM)의 출력을 검증할 수 있는 능력, 즉 ‘검증 가능성(checkability)’은 모델이 생성한 해답이 정확함을 독립적으로 판단할 수 있는 검증자(verifier)의 능력을 통해 정의됩니다. 이 논문에서는 검증 가능성을 높이기 위한 새로운 훈련 알고리즘을 제안하고, 이 알고리즘이 휴먼 검증자가 모델 출력을 더 쉽게 이해하고 정확하게 평가할 수 있게 돕는 방법을 연구합니다.
1.1 연구 배경과 필요성
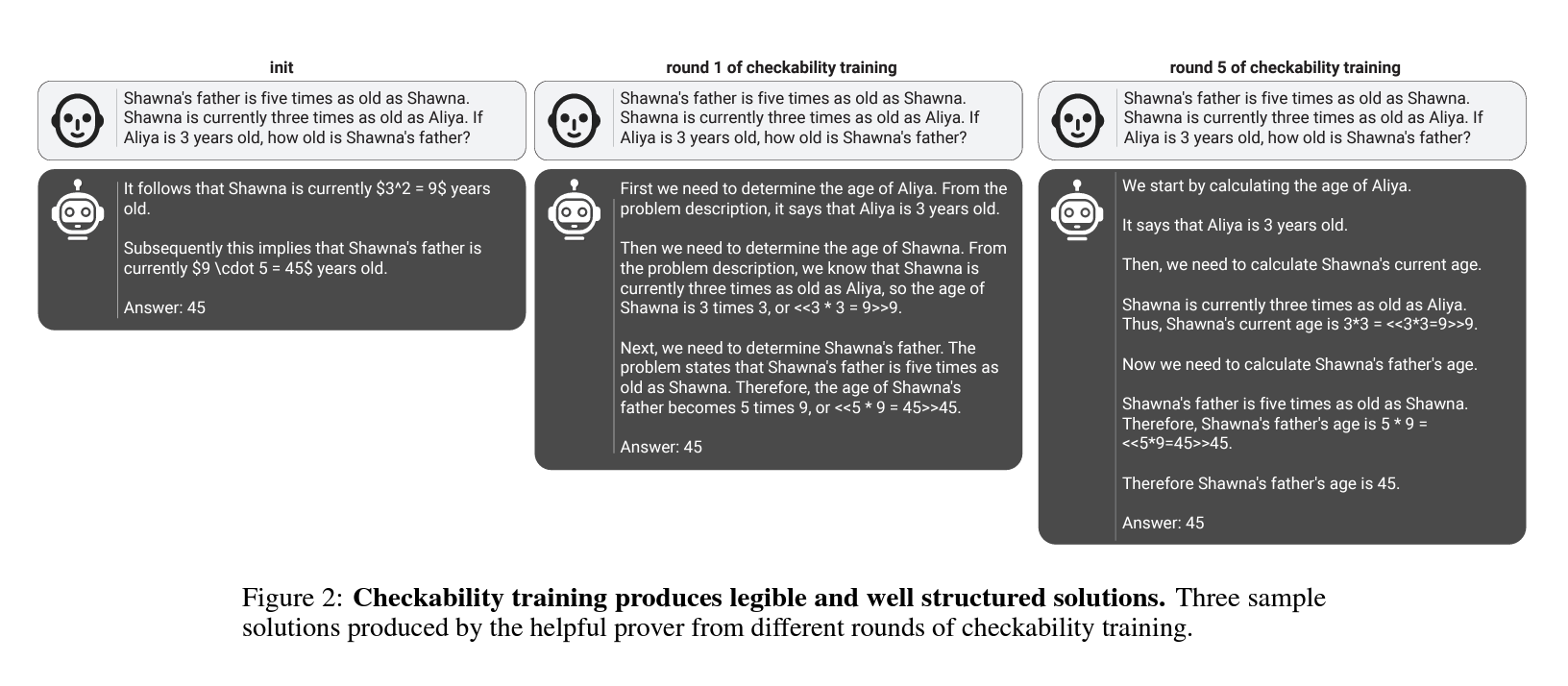
최근 LLM의 활용도가 높아짐에 따라, 이들 모델이 생성하는 출력의 정확성과 이해 가능성을 보장하는 것이 중요해지고 있습니다. 이런 문제의식에서 출발하여, 검증 가능하고 이해 가능한 해결책을 생성하는 모델을 개발하는 것이 연구의 목표입니다. 특히, 소규모 LLM을 활용하여 대규모 LLM의 출력이 휴먼에게 이해 가능하도록 하는 방법에 초점을 맞춥니다.
2. 관련 연구
검증자와 증명자 간의 상호 작용을 통한 검증 가능성 향상은 다양한 연구에서 다루어진 주제입니다. 이런 상호 작용은 주로 게임 이론적 접근을 통해 설명되며, 본 연구에서는 이런 기존 연구들을 바탕으로 하여 검증-증명자 게임(Prover-Verifier Game, PVG)을 발전시키는 데 중점을 둡니다. 특히, 골드와서 등의 연구에서 제안된 확률적-근사적 정확성(Probably-Approximately Correct, PAC) 검증 방식이 이 게임의 기초를 제공합니다.
3. 설정
데이터셋 \((x, y) \in \mathcal{X} \times \mathcal{Y}\)는 문제 설명 \(x\)와 이에 대한 유일하고 정확한 정답 \(y = y(x)\)을 포함합니다. 제안된 해결책 \(z\)에 대한 정확성 지표 \(\mathbf{1}_{\text{correct}}(x, z)\)는 다음과 같이 정의됩니다. \(\mathbf{1}_{\text{correct}}(x, z) = \begin{cases} 1 & \text{if } z \text{ is the same as } y(x) \\ 0 & \text{otherwise} \end{cases}\) 증명자(prover) \(\pi(z|x)\)는 주어진 문제 \(x\)에 대한 해결책을 제안하고, 검증자(verifier) \(v(x, z) \in [0, 1]\)는 이 해결책의 정답성을 평가합니다.
3.1 검증 가능성에서 PVG로
본 연구에서는 Cobbe 등이 제공한 등급 학교 수학 문제(grade-school math problems) 데이터셋을 사용하며, 이는 학습 초기 단계에서 검증자와 증명자 모델의 훈련에 사용됩니다. 이 데이터셋은 검증 가능성을 측정하고, 훈련 방법의 효과를 평가하는 데 중요한 벤치마크 역할을 합니다.
PVG에서는 두 플레이어, 즉 검증자와 증명자가 각각의 역할에 따라 행동하며, 이 게임은 다음과 같은 두 가지 주요 속성을 기반으로 합니다.
- 완전성(Completeness) 검증자는 증명자가 생성한 올바른 해결책을 항상 수용합니다. 모든 \(x \in \mathcal{X}\)에 대해, \(\mathbf{1}_{\text{correct}}(x, \pi(x)) = v(x, \pi(x)) = 1\)이 성립해야 합니다.
-
건전성(Soundness) 검증자는 모든 잘못된 해결책을 거부합니다. 모든 적대적 증명자 \(\pi'\)에 대해, 잘못된 해결책은 거부되어야 합니다.
\[\forall \pi' \in \mathcal{H}, \forall x \in \mathcal{X}, \mathbf{1}_{\text{correct}}(x, \pi'(x)) = 0 \Rightarrow v(x, \pi'(x)) = 0\]이는 건전성과 완전성이 높은 PVG를 통해 얻어진다고 가정합니다.
위와 같은 게임을 통해, 증명자는 정확하고 검증자에게 수용 가능한 해결책을 생성하도록 훈련되며, 검증자는 증명자가 제시한 해결책이 올바른지를 판단하는 능력이 향상됩니다.
검증자의 효용함수는 다음과 같이 정의됩니다.
\[R_V = -\frac{1}{2} \mathbb{E}_{x \sim P_{X}}[\ell(v(x, h(x)), \mathbf{1}_{\text{correct}}(x, h(x)))] - \frac{1}{2} \mathbb{E}_{x \sim P_{X}}[\ell(v(x, s(x)), \mathbf{1}_{\text{correct}}(x, s(x)))]\]\(\ell(v, c)\)는 교차 엔트로피 손실과 같은 손실 함수
증명자의 보상함수 \(R_P\)는 다음과 같이 정의됩니다.
\[R_P = \frac{1}{2} \mathbb{E}_{x \sim P_{X}}[r(v(x, h(x)), \mathbf{1}_{\text{correct}}(x, h(x)))] + \frac{1}{2} \mathbb{E}_{x \sim P_{X}}[r(v(x, s(x)), 1 - \mathbf{1}_{\text{correct}}(x, s(x)))]\]\(r(v, q)\)는 보상 함수로, 해결책의 정확성이 역할과 일치할 때 더 높은 보상을 줍니다.
[정리 1]Stackelberg 균형과 검증 가능성
\(\mathcal{H}\)가 \(\mathcal{X}\)에서 \(\mathcal{Z}\)로의 모든 결정적 매핑의 집합이라고 가정할 때, PVG에서 검증자의 유틸리티가 \(R_V\)이고 증명자의 유틸리티가 \(R_P\)인 경우, 완전성과 건전성 속성을 가진 검증자-리딩 스택켈버그 균형의 존재는 필요충분조건입니다.
이 정리는 증명자와 검증자가 각각 최적의 전략을 사용할 때 시스템의 건전성과 완전성이 보장됨을 의미합니다. 스택켈버그 균형은 한 플레이어(검증자)가 리더로서 전략을 설정하고, 다른 플레이어(증명자)가 이에 최적으로 응답한다는 개념입니다. 이 균형 상태에서는 어느 플레이어도 자신의 전략을 변경할 동기가 없습니다.
4. 결과 및 토론
검증자와 증명자 간의 반복적인 훈련을 통해, 검증 가능성이 점진적으로 향상됨을 확인할 수 있습니다. 검증자는 초기에 비해 훨씬 정확하게 증명자의 해결책을 평가할 수 있게 되며, 증명자는 더 정확하고 검증 가능한 해결책을 생성하게 됩니다. 이런 결과는 LLM의 출력이 휴먼에게 더 이해하기 쉽고, 따라서 더 신뢰할 수 있음을 시사합니다.
5. 결론
이 연구는 대규모 언어모델의 출력을 검증할 수 있는 새로운 방법을 제안하며, 이 방법은 검증자와 증명자 간의 상호작용을 통해 모델의 이해 가능성과 정확성을 향상시킬 수 있습니다.