Meta-Reasoning
- Related Project: Private
- Category: Paper Review
- Date: 2024-06-30
Meta-Reasoning: Semantics-Symbol Deconstruction for Large Language Models
- url: https://arxiv.org/abs/2306.17820
- pdf: https://arxiv.org/pdf/2306.17820
- html: https://arxiv.org/html/2306.17820v4
- abstract: Neural-symbolic methods have demonstrated efficiency in enhancing the reasoning abilities of large language models (LLMs). However, existing methods mainly rely on syntactically mapping natural languages to complete formal languages like Python and SQL. Those methods require that reasoning tasks be convertible into programs, which cater to the computer execution mindset and deviate from human reasoning habits. To broaden symbolic methods’ applicability and adaptability in the real world, we propose the Meta-Reasoning from a linguistic perspective. This method empowers LLMs to deconstruct reasoning-independent semantic information into generic symbolic representations, thereby efficiently capturing more generalized reasoning knowledge. We conduct extensive experiments on more than ten datasets encompassing conventional reasoning tasks like arithmetic, symbolic, and logical reasoning, and the more complex interactive reasoning tasks like theory-of-mind reasoning. Experimental results demonstrate that Meta-Reasoning significantly enhances in-context reasoning accuracy, learning efficiency, out-of-domain generalization, and output stability compared to the Chain-of-Thought technique. Code and data are publicly available at this https URL.
Contents
TL;DR
대규모 언어모델을 위한 의미-기호 분해를 통한 메타인퍼런스
- 메타인퍼런스은 의미 정보를 일반화된 기호적 표현으로 분해하여 대규모 언어모델(LLMs)의 인퍼런스 능력을 향상시키는 새로운 패러다임을 제안합니다.
- 이 방법은 기존 Chain-of-Thought(CoT) 기법과 비교하여, 복잡한 상호작용 인퍼런스 시나리오에서도 높은 정확도와 일반화 능력을 보여줍니다.
- 메타인퍼런스은 의미론적 해석을 최소화하고 기호를 중심으로 인퍼런스 구조를 재구성함으로써, 인퍼런스 과정의 데이터 효율성과 출력 안정성을 개선합니다.
1. 서론
- 기호는 휴먼이 자연과 사회의 복잡성을 이해하고 표현하는 기본 매체로 본 논문은 대규모 언어모델(LLMs)이 일반화된 인퍼런스 지식을 효과적으로 포착할 수 있도록 하는 새로운 메타인퍼런스 패러다임을 제안합니다.
- 현재의 인퍼런스 패러다임은 여러 학습 시연을 필요로 하며, 이는 LLM의 입력 용량과 인퍼런스 비용에 의해 제한됩니다. 이런 문제를 해결하기 위해, 의미 정보를 일반화된 기호적 표현으로 분해하여 LLM이 더 일반적인 지식을 획득하게 합니다.
2. 메타인퍼런스이란?
- 메타인퍼런스은 무한 의미 시스템에서 유한 기호 시스템으로의 전환을 목표로 하는 인퍼런스 패러다임으로 특정 의미 표현과 독립적이며 오직 기본적인 인퍼런스 골격만을 관련시키는 결과를 생성합니다.
- 메타인퍼런스의 핵심은 의미-기호 분해(Semantic-Symbolic Deconstruction)로, 이 과정은 원본 문제의 의미를 일반화된 의미로 전달하면서도 최종 결과에 영향을 주지 않습니다.

3. 메타인퍼런스 패러다임
- 의미 분해 규칙을 정의하고, 이를 통해 LLM이 문제를 간소화된 형태로 자동 학습할 수 있도록 하고, Chain-of-Thought(CoT) 기법과의 통합을 통해 LLM의 인퍼런스 능력을 극대화하는 것을 목표로 합니다
- 본 논문은 두 가지 융합 모드를 제안합니다.
- 완전 연속(Completely-serial)에서는 의미 분해를 수행한 후 해당 메타 질문에 대한 CoT를 작성하고,
- 교차 연속(Crossly-serial)에서는 원본 질문을 여러 하위 단계로 나누고 각각에 대해 의미 분해와 CoT를 적용합니다.
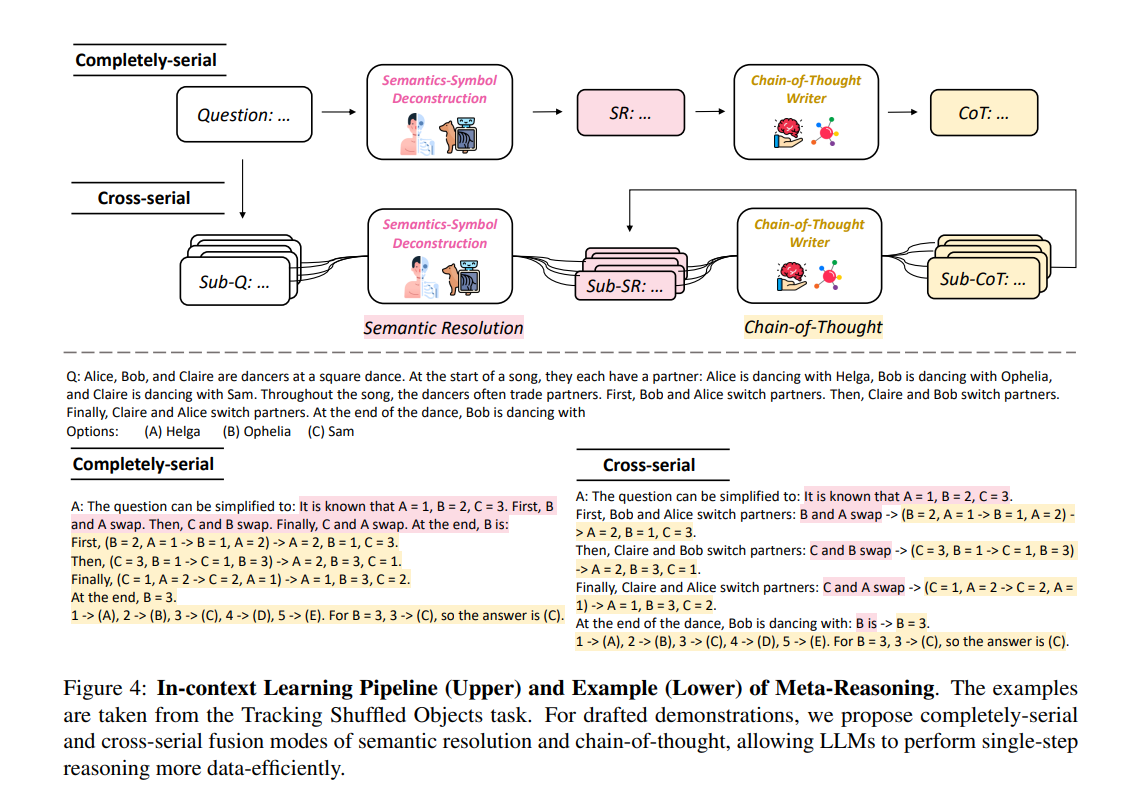
4. 수학적 정리 Entity와 Operation의 의미-기호 분해
4.1 Entity
Entity resolution은 주어진 문제에서 엔티티의 의미를 기호로 간소화하는 과정으로, 엔티티는 문제에 등장하는 주요 개체나 대상을 의미합니다. 텍스트 시퀀스 내의 엔티티는 불필요한 의미론적 정보를 제거하고 기본 기호로 치환됩니다. 예를 들어, “그는 3개의 사과를 먹었다”와 “그는 3개의 사과를 던졌다”는 모두 기본적으로 뺄셈 연산으로 간주될 수 있습니다.
\[\text{Entity resolution}: \mathcal{Q} \subset \Sigma^+, \sigma_{ij} = f_e([s_i:j])\]- \(\mathcal{Q}\)는 자연 언어 시스템 내 모든 기호적 표현을 포함하는 집합이며, \(\Sigma^+\)는 모든 가능한 문자열의 집합을 나타냅니다. \(\mathcal{Q} \subset \Sigma^+\)는 \(\mathcal{Q}\)가 \(\Sigma^+\)의 부분집합임을 의미하며, 즉 자연어 시스템의 모든 표현이 문자열 집합 내에 존재함을 나타냅니다.
- \(\sigma_{ij} = f_e([s_i:j])\)는 문장 내에서 특정 범위 \([s_i:j]\)에 해당하는 텍스트를 기호 \(\sigma_{ij}\)로 매핑하는 함수 \(f_e\)를 통해 변환합니다. 이 변환 과정은 복잡한 의미를 갖는 단어나 구를 간단한 기호로 요약하여 인퍼런스 과정을 단순화합니다.
4.2 Operation
Operation은 연산자들이 어떻게 엔티티 상태의 변화를 정의하고, 이 변화를 기호적으로 어떻게 나타낼 수 있는지에 대한 과정입니다. 연산자는 엔티티 상태의 정의(할당 및 논리적 연관성)와 변경(산술 연산)으로 축소되며, 각 연산을 자연어의 의미와 연결되는 기호로 표현하는 것을 가능하게 합니다.
\[\text{Operation resolution}: f_o: \mathcal{Q} \rightarrow \mathcal{O}_1 \cup \mathcal{O}_2, \rho_{ij} = f_o([s_i:j])\]연산자는 두 가지 주요 유형으로 나뉩니다.
- \(\mathcal{O}_1\): 엔티티 상태의 정의와 논리적 연관성을 나타내는 연산, 예를 들어 할당(=)이나 논리적 매핑(→) 등이 이에 해당합니다.
- \(\mathcal{O}_2\): 엔티티 상태의 변화를 나타내는 산술 연산, 예를 들어 더하기(+), 빼기(-), 곱하기(×), 나누기(÷) 등이 포함됩니다.
[Operation Resolution Process 상세]
- \(f_o: \mathcal{Q} \rightarrow \mathcal{O}_1 \cup \mathcal{O}_2\)는 주어진 자연 언어 표현을 해당 연산자 기호로 매핑하는 함수입니다. 이 함수는 문장에서 추출한 연산 표현을 기호적 연산으로 변환합니다.
- \(\rho_{ij} = f_o([s_i:j])\)는 문장 내에서 특정 범위 \([s_i:j]\)에 해당하는 연산 표현을 연산 기호 \(\rho_{ij}\)로 변환합니다. 이 과정은 복잡한 연산을 간단한 기호로 표현하여, 인퍼런스 과정에서 필요한 계산을 명확하고 간단하게 만들어 줍니다.
이런 변환은 LLM이 문제를 해석할 때 복잡한 자연 언어의 의미를 파악하는 대신, 기호적 표현을 사용하여 더 빠르고 효율적으로 인퍼런스할 수 있게 해 줍니다. 이는 또한 데이터의 효율성을 증가시키고, 일반화 및 인퍼런스 정확도를 개선하는 데 기여합니다.
위의 정의를 통해, 원래 질문의 복잡한 의미론적 구조를 간소화된 기호적 형태로 전환하고, 이를 통해 LLM이 보다 일반화된 인퍼런스 패턴을 학습하고 적용할 수 있도록 합니다.
5. 실험
- 산술, 기호, 논리적 인퍼런스 작업을 포함한 다양한 데이터셋에서 실험을 수행하고, 기존 CoT 기법과 비교하여 메타인퍼런스 방법이 모든 작업에서 성능이 향상되고,
- 특히 복잡한 상호작용 인퍼런스 시나리오에서 CoT 기법을 능가하며, 단일 시연으로도 높은 정확도를 보이는 것으로 확인했다고 합니다.
6. 장점 분석
- 메타인퍼런스은 범용 및 도메인 특화 인퍼런스에서의 일반화 능력을 강화해서 LLM이 새로운 과제에 대응할 수 있도록 지원하며, 출력 안정성도 향상시킵니다.
7. 토론 및 결론
- 메타인퍼런스은 특정 의미에 의존하는 인퍼런스 작업에는 적합하지 않을 수 있으나, 실제 에이전트 인퍼런스 시나리오에서 유망한 결과를 보여줍니다. 앞으로 더 포괄적인 인퍼런스 시나리오에서 그 적용 가능성을 더 깊이 탐구할 계획이라고 합니다.