Latent Diffusion Models | Bigger is not always better*

• Related Project: Private
• Category: Paper Review
• Date: 2024-04-05

Bigger is not Always Better: Scaling Properties of Latent Diffusion Models

• url: https://arxiv.org/abs/2404.01367
• pdf: https://arxiv.org/pdf/2404.01367
• html: https://arxiv.org/html/2404.01367v1
• abstract: We study the scaling properties of latent diffusion models (LDMs) with an emphasis on their sampling efficiency. While improved network architecture and inference algorithms have shown to effectively boost sampling efficiency of diffusion models, the role of model size – a critical determinant of sampling efficiency – has not been thoroughly examined. Through empirical analysis of established text-to-image diffusion models, we conduct an in-depth investigation into how model size influences sampling efficiency across varying sampling steps. Our findings unveil a surprising trend: when operating under a given inference budget, smaller models frequently outperform their larger equivalents in generating high-quality results. Moreover, we extend our study to demonstrate the generalizability of the these findings by applying various diffusion samplers, exploring diverse downstream tasks, evaluating post-distilled models, as well as comparing performance relative to training compute. These findings open up new pathways for the development of LDM scaling strategies which can be employed to enhance generative capabilities within limited inference budgets.
• keywords: Scaling Properties, Latent Diffusion Models

TL;DR

• 레이턴트 디퓨전 모델(Latent Diffusion Models, LDM)의 샘플링 효율성 분석
• 모델 크기와 샘플링 효율성 간의 관계 규명
• 소규모 모델이 동일한 샘플링 비용에서 대규모 모델보다 우수한 성능을 보임.

[서론]

LDM은 고품질의 대규모 데이터셋으로 학습된 우수한 생성 모델로, 이미지 합성 및 편집, 비디오 생성, 오디오 제작, 3D 합성 등 다양한 작업에서 우수한 성능을 보입니다. 그러나 실제 응용에서의 광범위한 배포를 저해하는 주요 장애물은 낮은 샘플링 효율성입니다. 이는 LDM이 고품질 출력을 생성하기 위해 다단계 샘플링에 의존하기 때문입니다. 예를 들어, 50단계 DDIM 샘플링을 사용하는 경우가 많으며, 이는 출력을 보장하지만 상당히 긴 지연 시간을 초래합니다.

최근의 연구는 모델 크기를 줄이고, 샘플링 단계를 줄여 샘플링 알고리즘을 개선하는 데 중점을 두고 있습니다. 특히, 확산 증류 기법은 다단계 샘플링 결과를 단일 전방 패스로 학습하여 샘플링 효율성을 높이는 방법입니다. 그러나 이런 기법들이 작은 모델의 샘플링 효율성을 충분히 탐구하지 않았습니다. 이 연구에서는 예산 제약 하에 39백만에서 5십억 개의 파라미터를 가진 12개의 텍스트-이미지 LDM을 학습하여 모델 크기가 샘플링 효율성에 미치는 영향을 조사합니다.

[문제와 해결 방법]

문제

LDM은 높은 품질의 출력을 위해 다단계 샘플링을 필요로 하며, 이로 인해 실시간 응용에서 사용이 제한됩니다. 특히, 소규모 모델의 샘플링 효율성에 대한 연구가 부족하여 모델 크기를 줄이는 과정에서 성능 저하를 최소화하는 방법이 필요합니다.

해결 방법

이 연구에서는 다양한 크기의 텍스트-이미지 LDM을 학습하고, 모델 크기가 샘플링 효율성에 미치는 영향을 평가합니다. 이를 통해 소규모 모델이 동일한 샘플링 비용 하에서 대규모 모델보다 효율적으로 작동할 수 있는 가능성을 탐구합니다.

선행 연구와 본 논문의 발견

선행 연구

• 확산 모델의 샘플링 효율성 향상: 다양한 네트워크 아키텍처와 샘플링 알고리즘의 개선을 통해 샘플링 단계를 줄이려는 시도
• 확산 증류 기법: 다단계 샘플링 결과를 단일 전방 패스로 학습하여 샘플링 효율성을 높이는 방법

본 논문의 발견

• 소규모 모델이 동일한 샘플링 비용에서 대규모 모델보다 우수한 성능을 보임.
• 모델 크기에 따른 샘플링 효율성의 차이가 다양한 샘플링 알고리즘에서도 일관되게 나타남.

[방법]

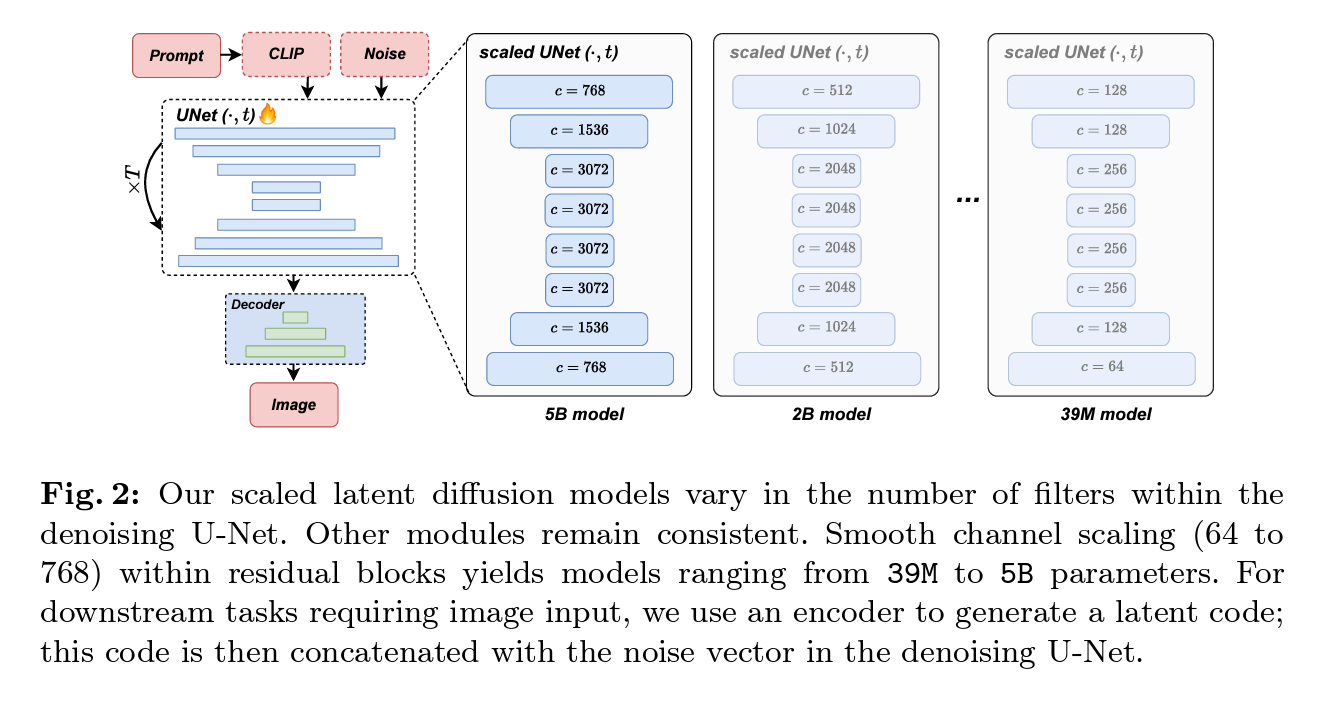
데이터셋 및 벤치마크

• 데이터셋: 약 6억 개의 텍스트-이미지 쌍으로 구성된 내부 데이터셋
• 벤치마크: COCO 2014 검증 세트(3만 개 샘플)와 DIV2K 검증 세트(3천 개 패치)에서 성능 평가

주요 방법

• 모델 크기 조정: 39백만에서 5십억 개의 파라미터를 가진 12개의 텍스트-이미지 LDM 학습
• 샘플링 효율성 평가: 다양한 모델 크기에서 샘플링 효율성을 평가하고, 소규모 모델의 성능을 분석
• 샘플링 알고리즘 비교: DDIM, DDPM, DPM-Solver++ 등의 샘플링 알고리즘 사용

[수학적 이해 및 논리]

LDM은 데이터 분포를 학습하여 새로운 데이터를 생성하는 모델로, 주로 이미지 생성에서 많이 사용됩니다. LDM의 주요 원리는 데이터에 점진적으로 노이즈를 추가하고, 반대로 그 노이즈를 제거하여 원본 데이터를 복원하는 과정입니다. 이를 통해 모델은 데이터 분포를 학습하고, 새로운 샘플을 생성할 수 있습니다. 이 과정은 확산 과정(diffusion process)과 역확산 과정(reverse diffusion process)으로 나뉩니다.

• 1. 확산 과정

  확산 과정에서는 데이터 $x_0$에 점진적으로 노이즈를 추가하여 점점 더 무작위화된 데이터 $x_T$를 생성하며, 다음과 같이 표현할 수 있습니다.

  \[q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_t} x_{t-1}, (1 - \alpha_t) \mathbf{I})\]

  상기 식에서 $ \alpha_t $는 노이즈 스케줄링 파라미터입니다. 이 과정은 다음과 같이 표현할 수 있습니다.

  \[x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon\]

  상기 식에서 $\epsilon \sim \mathcal{N}(0, \mathbf{I})$는 가우시안 노이즈입니다. 이 과정을 반복하면, 원본 데이터 $x_0$는 점점 더 많은 노이즈가 추가되어 $x_T$로 변환됩니다.

• 2. 역확산 과정

  역확산 과정에서는 노이즈가 추가된 데이터 $x_T$에서 점진적으로 노이즈를 제거하여 원본 데이터를 복원합니다. 이를 위해 모델 $\epsilon_\theta$가 학습되며, 다음과 같이 표현됩니다.

  \[p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I})\]

  상기 식에서 $\mu_\theta(x_t, t)$는 다음과 같이 정의됩니다.

  \[\mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right)\]

  $\bar{\alpha}_t$는 누적 노이즈 스케줄링 파라미터로, 다음과 같이 정의됩니다.

  \[\bar{\alpha}_t = \prod_{s=1}^t \alpha_s\]

  이제 역확산 과정을 통해 샘플링을 수행할 수 있습니다. 이를 수식으로 나타내면 다음과 같습니다.

  \[\hat{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \hat{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta(\hat{x}_t, t) \right) + \sigma_t z\]

  상기 식에서 $z \sim \mathcal{N}(0, \mathbf{I})$입니다. 이 과정을 $T$부터 1까지 반복하여 $\hat{x}_0$를 얻습니다.

• DDIM(Denoising Diffusion Implicit Model) 샘플링 위의 역확산 과정은 전통적인 DDPM(Denoising Diffusion Probabilistic Model) 샘플링 과정입니다. 그러나 효율성을 높이기 위해 DDIM(Denoising Diffusion Implicit Model) 샘플링 방법을 사용하기도 합니다. DDIM 샘플링은 다음과 같이 정의됩니다.

  \[\hat{x}_{t-1} = \sqrt{\alpha_{t-1}} \left( \frac{\hat{x}_t - \sqrt{1 - \alpha_t} \epsilon_\theta(\hat{x}_t, t)}{\sqrt{\alpha_t}} \right) + \sqrt{1 - \alpha_{t-1}} \epsilon_\theta(\hat{x}_t, t)\]

  DDIM 샘플링은 전통적인 DDPM 샘플링과 비교하여 더 적은 샘플링 단계로도 높은 품질의 결과를 얻을 수 있습니다. 이는 각 단계에서 더 많은 정보를 유지하면서 노이즈를 제거하기 때문입니다.

• 샘플링 효율성 LDM의 샘플링 효율성을 평가하기 위해, 다양한 크기의 모델을 비교합니다. 모델의 크기는 파라미터의 수로 결정되며, 이로 인해 샘플링 단계와 각 단계의 계산 비용이 달라집니다. 샘플링 비용은 다음과 같이 정의할 수 있습니다.

  \[\text{Sampling cost} = \text{Samping steps} \times \text{Cost per samping steps}\]

  상기 식에서, 모델의 크기가 커질수록 각 단계의 계산 비용이 증가합니다. 따라서 동일한 샘플링 비용 하에서 소규모 모델과 대규모 모델의 성능을 비교하여, 샘플링 효율성을 평가할 수 있습니다.

[실험]

다양한 크기의 LDM을 학습하여 샘플링 효율성을 평가한 결과, 소규모 모델이 동일한 샘플링 비용 하에서 대규모 모델보다 우수한 성능을 보였습니다. 이는 소규모 모델이 더 적은 계산 비용으로도 고품질의 출력을 생성할 수 있음을 시사합니다. 또한, 다양한 샘플링 알고리즘을 적용했을 때도 이런 경향이 일관되게 나타났습니다.

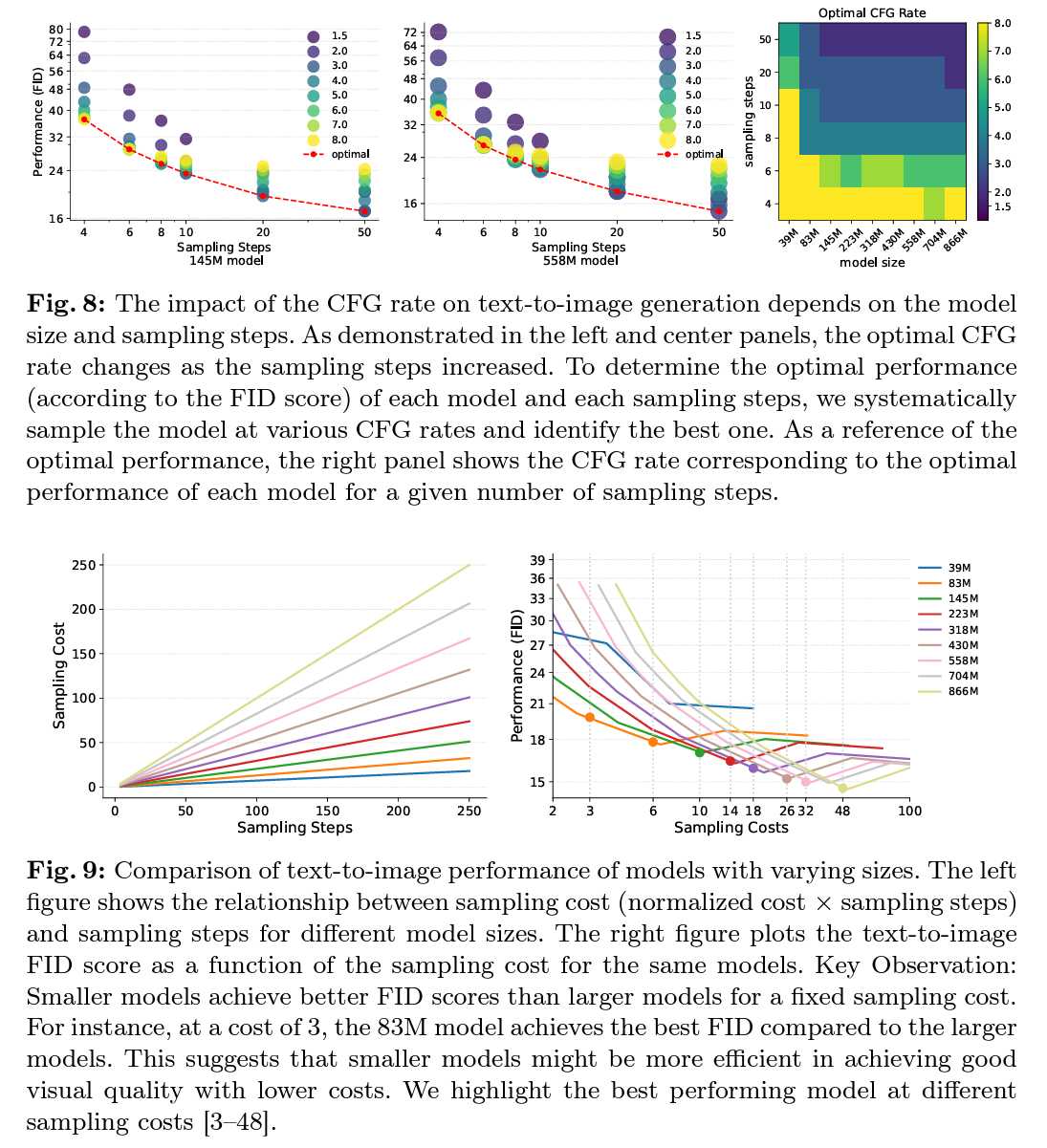
소규모 모델(39M)과 대규모 모델(5B)을 비교한 결과, 소규모 모델이 초기 샘플링 단계에서 더 나은 성능을 보였는데, 이는 제한된 샘플링 비용 하에서 소규모 모델이 더 효율적으로 작동할 수 있음을 시사할 수 있습니다.

[vLLM sLLM의 효용 색인마킹 - 파라미터 작은 모델의 효용성 Sampling]

• FID와 CLIP 점수: 모델 크기가 증가할수록 이미지 품질(FID)과 텍스트 일치도(CLIP) 점수가 개선
• 샘플링 비용 대비 성능: 동일한 샘플링 비용에서 소규모 모델이 대규모 모델보다 우수한 성능을 보임.

[결론]

이 논문에서는 LDM의 스케일링 특성을 조사하여, 소규모 모델이 동일한 샘플링 비용에서 대규모 모델보다 효율적으로 작동할 수 있음을 발견했습니다. 이는 실제 응용에서 모델 크기를 최적화하여 성능을 유지하면서 샘플링 효율성을 향상시키는 방향으로의 연구를 제시합니다. 다양한 샘플링 알고리즘에서도 이런 스케일링 특성이 일관되게 나타남을 확인하였다고 합니다.

[참고자료 1] 확산 모델과 노이즈 추가 및 제거 과정 이해

확산 모델은 데이터에 점진적으로 노이즈를 추가하고 다시 제거하여 원래 데이터를 복원하는 과정을 통해 학습합니다.

1. 확산 과정

• 확산 과정에서는 원본 데이터 \(x_0\)에 점진적으로 노이즈를 추가합니다.
• 이 과정은 데이터가 점점 더 무작위화되어 \(x_T\)에 가까워지도록 만듭니다.

확산 과정은 원래 데이터에 점진적으로 노이즈를 추가하는 단계입니다. 이 과정을 통해 데이터는 점점 무작위화되며, 최종적으로 완전히 무작위화된 데이터가 됩니다. 이 과정을 수식으로 표현하면 다음과 같습니다.

• 단위 행렬 \(\mathbf{I}\): 각 차원에서 독립적으로 노이즈를 추가하거나 제거합니다.
• $q(x_t \ x_{t-1})$: $x_{t-1}$라는 이전 단계의 데이터에서 $x_t$라는 현재 단계의 데이터를 생성하는 확률 분포를 나타냅니다.
• $\mathcal{N}(x_t; \sqrt{\alpha_t} x_{t-1}, (1 - \alpha_t) \mathbf{I})$: 이는 정규 분포(가우시안 분포)를 의미하며, $x_t$는 평균 $\sqrt{\alpha_t} x_{t-1}$를 가지며, 분산이 $(1 - \alpha_t) \mathbf{I}$인 분포를 따릅니다. (단위행렬 $mathbf{I}$는 확산 모델에서 데이터의 각 차원이 서로 독립적이고 동일한 분산을 가지도록 설정)
• \(\alpha_t\)는 노이즈 스케줄링 파라미터로, 각 단계에서 추가되는 노이즈의 비율을 조절합니다.
• \(\mathbf{I}\)는 단위 행렬로, 각 차원에서 노이즈가 독립적으로 추가됨을 의미합니다.

이를 좀 더 간단히 표현하면 다음과 같습니다.

• $x_t$: 현재 단계의 데이터
• $\sqrt{\alpha_t} x_{t-1}$: 이전 단계의 데이터에 노이즈 스케줄링 파라미터 $\alpha_t$를 적용한 값
• $\sqrt{1 - \alpha_t} \epsilon$: 가우시안 노이즈 $\epsilon$를 추가한 부분.
• $\epsilon \sim \mathcal{N}(0, \mathbf{I})$: 평균이 0이고 분산이 1인 정규 분포를 따르는 노이즈

이 과정을 여러 번 반복하면 원래 데이터 $x_0$는 점점 더 많은 노이즈가 추가되어 $x_T$라는 무작위화된 데이터가 됩니다.

예시

• 원본 데이터 \(x_0\)가 \([1, 2]\)라고 가정하고 다음 예시를 살펴보면

• (예시1) 첫 번째 단계에서 \(\alpha_1 = 0.9\)인 경우

  \(x_1 = \sqrt{0.9} \cdot x_0 + \sqrt{1 - 0.9} \cdot \epsilon\)
  위 식에서 \(\epsilon\)은 평균이 0이고 분산이 1인 가우시안 노이즈입니다.

• (예시2) \(\epsilon = [0.5, -0.5]\)인 경우

  \(x_1 = \sqrt{0.9} \cdot [1, 2] + \sqrt{0.1} \cdot [0.5, -0.5]\)
  \(x_1 = [0.95, 1.90] + [0.158, -0.158]\)
  \(x_1 = [1.108, 1.742]\)

• 반복
  • 위 과정을 반복하여 \(x_T\)에 도달하게 됩니다.
  • 각 단계마다 조금씩 더 많은 노이즈가 추가되어 데이터가 점점 더 무작위화됩니다.

2. 역확산 과정

역확산 과정에서는 노이즈가 추가된 데이터 $x_T$에서 점진적으로 노이즈를 제거하여 원본 데이터를 복원

기본 개념

• 역확산 과정에서는 노이즈가 추가된 데이터 \(x_T\)에서 점진적으로 노이즈를 제거하여 원본 데이터 \(x_0\)로 복원합니다.
• 이를 위해 모델 \(\epsilon_\theta\)가 학습됩니다.

역확산 과정은 노이즈가 추가된 데이터에서 점진적으로 노이즈를 제거하여 원래 데이터를 복원하는 단계로 식으로 표현하면 다음과 같습니다.

• $p_\theta(x_{t-1} | x_t)$: $x_t$라는 현재 단계의 데이터에서 $x_{t-1}$라는 이전 단계의 데이터를 생성하는 확률 분포를 나타냅니다.
• \(\sigma_t^2 \mathbf{I}\)는 추가적인 노이즈의 분산을 나타냅니다.
• $\mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma_t^2 \mathbf{I})$: 정규 분포로, $x_{t-1}$는 평균 $\mu_\theta(x_t, t)$를 가지며, 분산이 $\sigma_t^2 \mathbf{I}$인 분포를 따릅니다.
• $\mu_\theta(x_t, t)$: 모델이 예측하는 평균값으로, 다음과 같이 정의됩니다.

• $\mu_\theta(x_t, t)$: 현재 단계의 데이터 $x_t$와 시간 $t$를 입력으로 받아, 이전 단계의 데이터 $x_{t-1}$의 평균값을 계산합니다.
• $\alpha_t$: 앞서 설명한 각 스텝별 노이즈 스케줄링 파라미터.
• $\bar{\alpha}_t$: 누적 노이즈 스케줄링 파라미터로, 다음과 같이 정의됩니다.

이제 역확산 과정을 통해 샘플링을 수행하는 방법을 살펴보면 다음과 같습니다.

• $\hat{x}_{t-1}$: 현재 단계의 데이터 $\hat{x}_t$에서 노이즈를 제거하여 얻은 이전 단계의 데이터.
• $\sigma_t z$: 가우시안 노이즈 $z \sim \mathcal{N}(0, \mathbf{I})$를 추가하여 불확실성을 반영.

이 과정을 $T$부터 1까지 반복하여 $\hat{x}_0$를 얻으면, 최종적으로 원래 데이터 $x_0$를 복원할 수 있습니다.

예시 \(x_T\)에서 시작하여, 각 단계에서 노이즈를 제거합니다.

• (예시1) 예를 들어, \(x_T = [1.108, 1.742]\)이고, \(t = T\), \(\alpha_T = 0.9\)인 경우

  \(\hat{x}_{T-1} = \frac{1}{\sqrt{0.9}} \left( x_T - \frac{1 - 0.9}{\sqrt{1 - \bar{\alpha}_T}} \epsilon_\theta(x_T, T) \right) + \sigma_T z\)
  위 식에서 \(\epsilon_\theta(x_T, T)\)는 모델이 예측한 노이즈, \(z\)는 새로운 가우시안 노이즈입니다.

• (예시2) \(\epsilon_\theta(x_T, T) = [0.1, -0.1]\)이고, \(z = [0.1, 0.1]\)인 경우

  \(\hat{x}_{T-1} = \frac{1}{\sqrt{0.9}} \left( [1.108, 1.742] - \frac{0.1}{\sqrt{1 - \bar{\alpha}_T}} \cdot [0.1, -0.1] \right) + \sigma_T [0.1, 0.1]\)
  기호는 첫 번째 예시와 동일하며, 이 과정을 반복하여 \(\hat{x}_0\)에 도달하게 됩니다.

3. 데이터의 점진적 변형 및 복원(확산 및 역확산의 반복)

결론적으로 확산 및 역확산 과정을 반복하여 원래 데이터를 점진적으로 변형하고 복원할 수 있습니다.

• 확산 과정: 데이터에 점진적으로 노이즈를 추가하여 무작위화된 데이터를 생성하는 과정. 원본 데이터 \(x_0\)에 점진적으로 노이즈를 추가하여 무작위화된 데이터 \(x_T\)를 생성
• 역확산 과정: 노이즈가 추가된 데이터에서 노이즈를 제거하여 원래 데이터를 복원하는 과정. 노이즈가 추가된 데이터 \(x_T\)에서 점진적으로 노이즈를 제거하여 원본 데이터 \(x_0\)를 복원 각 과정은 정규 분포를 사용하여 수학적으로 표현되며, 노이즈 스케줄링 파라미터 $\alpha_t$를 사용하여 조절됩니다.