Inner Working**

• Related Project: Private
• Category: Paper Review
• Date: 2024-05-01

A Primer on the Inner Workings of Transformer-based Language Models

• url: https://arxiv.org/abs/2405.00208
• pdf: https://arxiv.org/pdf/2405.00208
• html https://arxiv.org/html/2405.00208v2
• abstract: The rapid progress of research aimed at interpreting the inner workings of advanced language models has highlighted a need for contextualizing the insights gained from years of work in this area. This primer provides a concise technical introduction to the current techniques used to interpret the inner workings of Transformer-based language models, focusing on the generative decoder-only architecture. We conclude by presenting a comprehensive overview of the known internal mechanisms implemented by these models, uncovering connections across popular approaches and active research directions in this area.

[수학적 논증 핵심 색인마킹]

[Anthropic toymodel 및 Llama-3에서 safety 제거한 포스트 등 참조]

Contents

• A Primer on the Inner Workings of Transformer-based Language Models
  • TL;DR

TL;DR

• 대규모 언어모델의 복잡한 구조와 작동 원리를 이해하기 위해 다각적인 측면에서 검토합니다.
• 이 논문은 LLM의 내부 표현에서 구체적인 특징들을 파악하고, 어휘 토큰과의 상호작용을 분석하는 다양한 기술을 제안하며, 정보 디코딩(Information Decoding)과 어휘 공간에서의 디코딩(Decoding in Vocabulary Space) 두 가지 주요 접근 방식을 중심으로 트랜스포머의 내부 작동 원리를 탐구합니다.

[신경망의 이해]

딥러닝 분야에서, 특히 대규모 언어모델(LLM)의 복잡한 구조와 내부 작동 원리를 이해하는 것은 근본적인 챌린지입니다. 이런 해석 가능성의 부족은 모델이 어떻게 결론에 이르는지에 대한 깊은 통찰을 얻는 것을 방해할 뿐만 아니라, 잠재적인 편향을 디버깅하는 데도 장애가 됩니다.

[전통적인 탐사 방법을 넘어서: 다양한 기술의 스펙트럼]

본 논문은 네트워크의 내부 표현에서 특정 특징들을 예측하기 위해 보조 모델을 훈련하는 전통적인 탐사 기법(probing techniques)을 넘어섭니다. 이런 방법들은 특정 특징의 존재를 나타낼 수 있지만, LLM이 실제로 예측을 위해 그 특징들을 활성화한다는 것을 보장하지는 않습니다.

이 연구는 두 가지 주요 접근 방식으로 분류된 더 넓은 기술 스펙트럼을 제시합니다.

• 1) 정보 디코딩(Information Decoding): 이 접근 방식은 LLM의 내부 표현에 인코딩된 구체적인 특징들을 이해하고자 합니다. 이는 선형 표현 가설(linear representation hypothesis)을 바탕으로, 특징들이 표현 공간 내의 선형 부공간으로 인코딩된다고 가정합니다. 선형 특징 삭제(linear feature erasure) 및 조종 생성(steering generation)과 같은 기술은 내부 표현을 조작하여 이런 인코딩된 특징들을 분리하고 분석합니다. 복잡성을 다루기 위해, 이 연구는 희소 오토인코더(sparse autoencoders, SAEs) 및 관문 변형인 관문 희소 오토인코더(gated sparse autoencoders, GSAEs)의 사용을 탐구하여 특징들을 분리하고 복구 정확도를 향상시키고자 합니다.
• 2) 어휘 공간에서의 디코딩(Decoding in Vocabulary Space): 이 접근 방식은 LLM이 어휘 토큰과 상호작용하는 방식을 분석하는 데 초점을 맞춥니다. 이는 로그잇 렌즈(logit lens) 및 패치스코프(patchscopes) 같은 기술을 포함하여 네트워크 내의 중간 표현에서 정보를 디코딩하는 기법을 포괄합니다. 추가로, 모델의 가중치 행렬에서 정보를 디코딩하는 방법, 특이값 분해(singular value decomposition, SVD) 및 로그잇 분광(logit spectroscopy)를 탐구합니다. 마지막으로, 특정 네트워크 기능을 가장 강하게 활성화하는 입력을 식별하는 최대 활성화 입력(maximally-activating inputs) 개념을 조사합니다.

[결론]

이 연구는 다양한 기술을 종합적으로 검토함으로써 연구자들에게 LLM에서의 정보 처리를 탐사하는 강력한 도구를 제공합니다. 수학적 기반에 중점을 두고 방법 간의 논리적 연결을 다리는 이 접근 방식은 해석 가능성 연구에서의 진전을 위한 길을 열어줍니다.

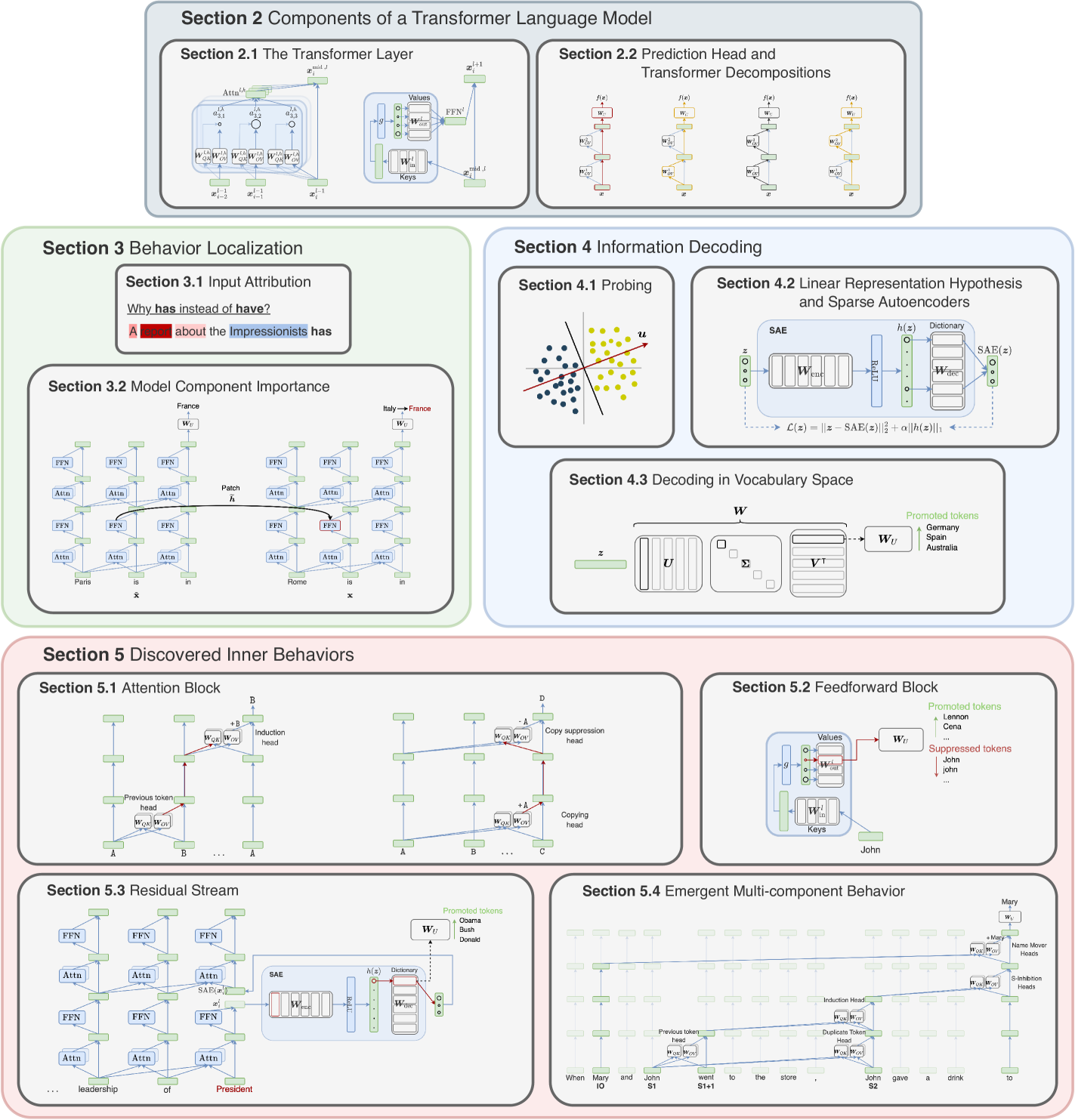
[상세]

1. 분산 정렬 검색(Distributed Alignment Search, DAS)

• 분산 정렬 검색(DAS)은 신경망의 저차원 표현 공간에서 인과적으로 중요한 특성을 찾기 위해 개발된 방법입니다. 이 방법은 비기준 정렬된(subspace not aligned with the standard basis) 부분공간에서의 분산된 개입을 통해 이루어집니다.

• 선행 연구: DAS는 저차원 표현 공간에서의 그래디언트 하강법을 이용하여 비기준 정렬된 부분공간을 찾고, 이 공간에서 분산 개입을 수행합니다. 이런 개입은 목표하는 문법 평가 및 개별 속성의 인과 효과 분리에 효과적임이 입증되었습니다.

2. 인과적 대리 모델(Causal Proxy Models, CPMs)

• 인과적 대리 모델(CPMs)은 저수준 모델의 예측을 모방하고, 대상 개입 후의 반사실적 행동을 시뮬레이션하기 위해 훈련된 모델입니다.

• 선행 연구: CPM은 주어진 데이터에 대한 모델의 반응을 예측하는 대리 모델로, 원래 모델의 특정 층에서 정보를 추출하여 인과적 개입을 시뮬레이션합니다. 이는 복잡한 모델의 예측과정을 단순화하여 해석 가능하게 만듭니다.

3. 정보 디코딩

• 모델이 어떤 정보를 추출하고 처리하는지를 이해함으로써, 모델의 예측 메커니즘을 깊이 있게 분석하는 접근 방식입니다.

• 선행 연구: 정보 디코딩은 네트워크에서 각 컴포넌트가 처리하는 정보의 종류와 방식을 분석합니다. 이는 주로 중간 표현을 통한 정보의 특성을 매핑하고, 이를 통해 모델이 어떻게 정보를 인코딩하는지를 파악하는 데 사용됩니다.

4. 프로빙(Probing)

• 프로빙은 신경망의 내부 표현을 분석하는 도구로, 입력 속성에서 중간 표현으로의 매핑을 평가합니다.

• 선행 연구: 프로브는 중간 표현에서 입력 속성의 정보를 얼마나 잘 인코딩하는지를 평가하는 감독된 모델입니다. 이를 통해 표현에 인코딩된 정보의 양을 수량화하고, 프로브가 학습하는 과정에서의 정보 처리 효율성을 분석합니다.

5. 선형 표현 가설과 희소 오토인코더

• 선형 표현 가설은 특성이 표현 공간의 선형 부분공간으로 인코딩된다고 언급합니다.

• 선행 연구: 이 가설은 주로 단어 임베딩에서 선형적 문법적/의미적 관계를 포착하는 연구로부터 지지받습니다. 예를 들어, ‘Spain’과 ‘Madrid’ 사이의 벡터 차이를 ‘France’ 벡터에 더하면 ‘Paris’에 근접한 벡터가 결과로 나타납니다. 이는 ‘capital_of’라는 추상적 특성의 방향으로 해석될 수 있습니다.

6. 스티어링 생성과 선형 개입

• 모델의 예측에 대한 명확한 인과적 해석을 제공하기 위해 사용되는 기술입니다.

• 선행 연구: 스티어링 생성은 모델의 예측에 영향을 미치는 특성의 방향을 조작하여 구현됩니다. 예를 들어, 감성의 방향을 반대로 조정함으로써, 모델이 반대 감성의 텍스트를 생성하도록 유도할 수 있습니다. 이는 주로 선형 분류기를 사용하여 특성의 방향을 학습하고, 이를 모델 입력에 적용하여 변경된 출력을 생성하는 방식으로 이루어집니다.

7. LM Interpretability Tools

이 섹션에서는 Transformer 기반 언어 모델의 해석 가능성 연구를 지원하기 위해 소개된 여러 오픈 소스 소프트웨어 라이브러리들을 요약하고, 각각의 주요 강점을 강조합니다.

• 입력 속성 도구 (Input Attribution Tools)

  • Captum (Kokhlikyan et al., 2020): Pytorch 기반의 라이브러리로, 그래디언트와 섭동 기반의 입력 속성 방법들을 제공합니다. 특히, Captum은 입력 속성에 대한 수학적 방법으로 training dataset 속성 방법을 지원하며, 이는 모델 예측에 기여하는 입력 데이터의 요소를 정량화합니다.
  • SHAP (Lundberg & Lee, 2017): 모델 비종속적인 설명을 지원하는 도구로, 주로 섭동 기반 방법을 사용하여 입력 변수가 예측에 미치는 영향을 계산합니다. 이는 샴(SHAP) 값으로 표현되어, 각 기능이 예측 결과에 미치는 평균적인 기여도를 나타냅니다.
  • Saliency (PAIR Team, 2023): 주로 그래디언트 기반 입력 속성 방법을 제공하며, 입력 변수의 중요도를 평가하기 위해 각 변수에 대한 출력의 민감도를 계산합니다.

• 구성 요소 중요성 분석 도구 (Component Importance Analysis Tools)

  • TransformerLens (Nanda & Bloom, 2022): 모델 활성화 및 어텐션 계층을 분해하여 맞춤형 개입을 용이하게 하는 후크 포인트를 제공하는 도구입니다. 이는 Transformer 모델의 주요 구성 요소의 중요성을 이해하는 데 도움을 줍니다.
  • Pyvene (Wu et al., 2024c): 복잡한 개입 계획을 지원하는 라이브러리로, 훈련 중 개입과 같은 기능을 제공하여 모델의 동작을 수정하고 성능을 최적화할 수 있습니다.

• 모델 내부 시각화 도구 (Tools for Visualizing Model Internals)

  • BERTViz (Vig, 2019) 및 exBERT (Hoover et al., 2020): Transformer 기반 모델의 주목 가중치와 활성화 상태를 시각화하여 모델이 어떤 정보를 중요하게 여기는지 분석합니다.

  • LM-Debugger (Geva et al., 2022a): 중간 표현의 업데이트를 로짓 기여도(logit attribution)를 통해 검토하는 도구입니다. 이는 다음과 같은 식을 사용하여 각 구성 요소의 출력이 최종 예측에 미치는 영향을 계산합니다.

    \[\text{logit attribution} = \sum_{i} w_i x_i\]

    수식에서 \(w_i\)는 가중치, \(x_i\)는 입력 특성입니다.

• 기타 주목할 만한 해석 가능성 관련 도구

  • RASP 및 Tracr (Weiss et al., 2021; Lindner et al., 2023): Transformer 계산을 휴먼이 읽을 수 있는 언어로 변환하고, 특정 동작을 구현하는 소형 Transformer 모델을 자동 생성하는 컴파일러를 제공합니다.
  • Pyreft (Wu et al., 2024b): 훈련 가능한 개입을 조정하고 공유하여 선택된 작업에 대한 언어 모델의 성능을 최적화하는 도구입니다.

결론 및 향후 방향 (Conclusion and Future Directions)

이 논문에서는 Transformer 기반 언어 모델을 이해하는 데 유용한 해석 가능성 방법을 개관하고, 이들이 이끌어낸 통찰력을 제시했습니다. 이런 도구들은 모델의 구성 요소 간 복잡한 상호작용과 이들이 예측에 미치는 영향을 보다 명확하게 이해하는 데 기여하며, 이는 모델의 안전성과 신뢰성을 향상시키는 데 중요할 수 있습니다.

[참고자료 1] 트랜스포머 언어 모델의 구성 요소

오토회귀 언어 모델은 토큰 시퀀스에 확률을 할당합니다. 확률 연쇄 규칙을 사용하여 시퀀스 \(\mathbf{t} = \langle t_1, t_2, \ldots, t_n \rangle\) 에 대한 확률 분포를 조건부 분포의 곱으로 분해할 수 있습니다.

이런 분포는 학습에 사용되는 코퍼스의 가능성을 최대화하도록 최적화된 신경망을 사용하여 파라미터화할 수 있습니다. (Bengio et al., 2003) 최근 몇 년 동안 Vaswani et al. (2017)의 트랜스포머 아키텍처는 그 표현력과 확장성 덕분에 이 목적을 위해 널리 채택되었습니다. (Kaplan et al., 2020) 여러 변형된 트랜스포머가 제안되었지만, 성능으로 인해 큰 사랑을 받고 있는 디코더 전용 아키텍처(일명 GPT 유사)에 초점을 맞춥니다.

임베딩은 입력된 단어를 숫자로 된 벡터로 변환합니다. 각 단어는 고유한 벡터(임베딩)로 표현되며, 이는 모델이 단어 간의 관계를 학습하는 데 도움이 됩니다. 예를 들어, 단어 “고양이”와 “강아지”는 서로 비슷한 벡터로 변환됩니다.

1. 디코더 전용 모델

디코더 전용 모델 \(f\)는 \(L\)개의 레이어을 가지며, 토큰 \(\mathbf{t} = \langle t_1, t_2, \ldots, t_n \rangle\)을 나타내는 임베딩 시퀀스 \(\mathbf{x} = \langle \mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n \rangle\)에서 작동합니다. 각 임베딩 \(\mathbf{x} \in \mathbb{R}^d\)는 임베딩 행렬 \(\mathbf{W}_E \in \mathbb{R}^{\|\mathcal{V}\| \times d}\)의 행에 해당하는 행 벡터로, \(\mathcal{V}\)는 모델 어휘입니다. 예를 들어, 위치 \(i\)와 레이어 \(l\)에서의 중간 레이어 표현은 \(\mathbf{x}_i^l\)로 나타냅니다.

\(\mathbf{X} \in \mathbb{R}^{n \times d}\)로 임베딩이 행으로 쌓인 행렬로 시퀀스 \(\mathbf{x}\)를 나타냅니다. 마찬가지로, 중간 표현에서는 \(\mathbf{X}_{\leq i}^l\)가 위치 \(i\)까지의 레이어 \(l\)의 표현 행렬을 나타냅니다.

2. 잔차 스트림 관점

트랜스포머에서의 해석 가능성에 관한 최근 문헌에 따르면, 잔차 스트림 관점을 채택하여 아키텍처를 설명합니다. (Elhage et al., 2021a) 이 관점에서 각 입력 임베딩은 주의(attention) 블록(섹션 2.1.2)과 피드포워드 블록(섹션 2.1.3)으로부터의 벡터 덧셈을 통해 업데이트되어 잔차 스트림 상태(또는 중간 표현)를 생성합니다. 마지막 레이어 잔차 스트림 상태는 언임베딩 행렬 \(\mathbf{W}_U \in \mathbb{R}^d \times \|\mathcal{V}\|\)를 통해 어휘 공간으로 투영되고, 소프트맥스 함수로 정규화되어 새 토큰을 샘플링하는 어휘에 대한 확률 분포를 얻습니다.

2.1.1 레이어 정규화 (Layer Normalization)

각 레이어의 입력을 정규화하여 모델이 안정적으로 학습할 수 있도록 합니다. 정규화는 각 벡터의 평균을 빼고, 표준 편차로 나누는 방식으로 이루어집니다.

레이어 정규화(LayerNorm)는 딥 뉴럴 네트워크의 학습 과정을 안정화하는 데 사용되는 일반적인 연산입니다. (Ba et al., 2016) 초기 트랜스포머 모델은 각 블록의 출력에서 LayerNorm을 구현했지만, 최신 모델은 일관되게 각 블록 앞에 정규화를 수행합니다. (Xiong et al., 2020; Takase et al., 2023) 주어진 표현 \(\mathbf{z}\)에 대해 LayerNorm은 다음과 같이 계산됩니다.

\(\mu\)와 \(\sigma\)는 각각 평균과 표준 편차를 계산하고, \(\gamma \in \mathbb{R}^d\)와 \(\beta \in \mathbb{R}^d\)는 학습된 요소별 변환 및 바이어스를 나타냅니다. 레이어 정규화는 입력 표현을 \([1, 1, \ldots, 1] \in \mathbb{R}^d\)의 법 벡터에 의해 정의된 초평면에 투영하는 평균 빼기 연산으로 시각화할 수 있으며, 결과 표현을 초구로 매핑하는 스케일링으로 해석할 수 있습니다. (Brody et al., 2023) Kobayashi et al. (2021)은 LayerNorm을 \(\mathbf{z} \mathbf{L} + \beta\)로 처리할 수 있다고 언급하였으며, 이때 \(\sigma(\mathbf{z})\)는 상수로 간주됩니다. (Appendix B) 이 관점에서 행렬 \(\mathbf{L}\)는 중심화 및 스케일링 연산을 계산합니다. 또한, 아핀 변환의 가중치는 다음 선형 계층으로 접을 수 있어 분석을 단순화할 수 있습니다. (Appendix C)

현재 Llama 2(Touvron et al., 2023)와 같은 최신 언어 모델은 중심화 연산을 제거하고 루트 평균 제곱(RMS) 통계를 사용하여 스케일링을 수행하는 대안적인 층 정규화 절차인 RMSNorm(Zhang & Sennrich, 2019)을 채택하고 있습니다.

2.1.2 어텐션 메커니즘

어텐션 메커니즘은 모델이 입력 시퀀스의 각 단어가 다른 단어들과 어떻게 연관되는지를 학습하는 부분입니다. 예를 들어, 문장에서 “나는 사과를 먹었다”라는 문장이 주어지면, 어텐션 메커니즘은 “사과”와 “먹었다”가 연관이 있음을 학습합니다.

트랜스포머 계층의 핵심 구성 요소 중 하나는 어텐션 메커니즘입니다. 이는 각 토큰이 입력 시퀀스의 다른 모든 토큰과의 관계를 학습하도록 도와줍니다. 어텐션은 다음과 같이 계산됩니다.

• 쿼리, 키, 값 계산: 주어진 입력 \(\mathbf{X}\)에 대해 쿼리 \(\mathbf{Q}\), 키 \(\mathbf{K}\), 값을 계산합니다. 쿼리와 키의 내적을 통해 어텐션 스코어를 계산합니다. 그런 다음 소프트맥스를 사용하여 정규화합니다.

• 어텐션 스코어 계산: 쿼리와 키의 내적을 통해 어텐션 스코어를 계산합니다.

  \[\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left( \frac{\mathbf{Q} \mathbf{K}^T}{\sqrt{d_k}} \right) \mathbf{V}\]

• 멀티-헤드 어텐션: 다양한 어텐션 헤드를 통해 정보를 종합합니다.

여러 개의 어텐션 헤드를 사용하여 다양한 관계를 학습합니다. 각 헤드는 독립적으로 어텐션을 계산한 후, 결과를 합칩니다.

\(\text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h) \mathbf{W}_O\) 각 어텐션 헤드는 서로 다른 \(\mathbf{W}_Q, \mathbf{W}_K, \mathbf{W}_V\)를 사용하여 계산됩니다.

2.1.3 피드포워드 네트워크

어텐션 메커니즘 후에는 피드포워드 네트워크가 따라옵니다. 이는 두 개의 선형 변환과 그 사이의 활성화 함수로 구성됩니다.

어텐션 후에는 피드포워드 네트워크를 통해 각 단어의 벡터를 변환합니다. 이는 단순한 두 개의 선형 변환과 활성화 함수로 이루어져 있습니다.

이 계층은 입력을 처리하여 모델의 표현력을 향상시킵니다.

2.2 언임베딩 및 소프트맥스

변환된 벡터를 다시 단어 공간으로 변환하고, 소프트맥스를 사용하여 다음 단어의 확률을 계산합니다.

마지막 레이어의 잔차 스트림 상태는 언임베딩 행렬 \(\mathbf{W}_U \in \mathbb{R}^d \times \|\mathcal{V}\|\)을 통해 어휘 공간으로 투영됩니다. 그런 다음 소프트맥스 함수를 통해 정규화되어 새로운 토큰을 샘플링할 확률 분포를 얻습니다.

[참고자료 2] Attention Mechanism in Transformers

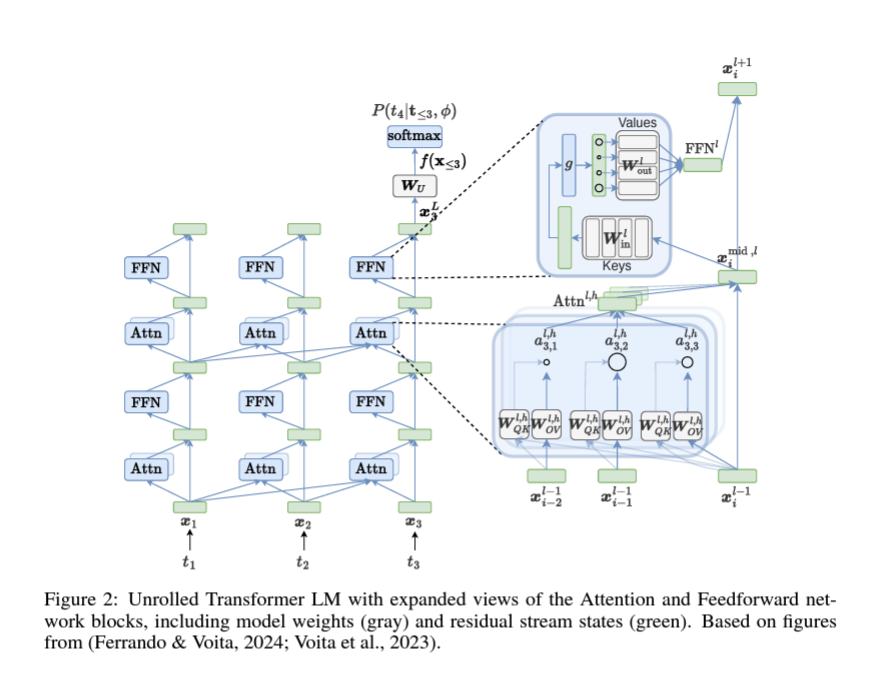
Attention은 Transformer 모델에서 각 레이어의 토큰 표현을 맥락화하는 중요한 메커니즘입니다. Attention 블록은 다중 Attention 헤드로 구성됩니다. 디코딩 단계 \(i\)에서, 각 Attention 헤드는 이전 위치(\(\leq i\))의 잔류 스트림을 읽고, 어떤 위치에 주의를 기울일지 결정한 후, 해당 위치에서 정보를 수집하고 이를 현재 잔류 스트림에 기록합니다. Kobayashi et al. (2021) 및 Elhage et al. (2021a)가 제안한 재배열을 채택하여 잔류 스트림 기여도를 단순화합니다.

1. Attention Head 계산

각 Attention 헤드는 다음과 같이 계산됩니다.

• \(\text{Attn}_{l, h}(X_{\leq i}^{l-1})\): 레이어 \(l\)의 헤드 \(h\)에서 현재 위치 \(i\)까지의 입력 \(X_{\leq i}^{l-1}\)에 대한 Attention 결과
• \(a_{i,j}^{l,h}\): 헤드 \(h\)의 위치 \(i\)에서 위치 \(j\)로의 Attention 가중치
• \(x_{j}^{l-1}\): 레이어 \(l-1\)에서의 위치 \(j\)의 입력 벡터
• \(W_{V}^{l,h}\): 레이어 \(l\)의 헤드 \(h\)에 대한 값(Value) 가중치 행렬
• \(W_{O}^{l,h}\): 레이어 \(l\)의 헤드 \(h\)에 대한 출력(Output) 가중치 행렬

학습 가능한 가중치 행렬 \(W_{V}^{l,h} \in \mathbb{R}^{d \times d_h}\)와 \(W_{O}^{l,h} \in \mathbb{R}^{d_h \times d}\)는 OV 행렬로 결합됩니다.

이를 OV (output-value) 회로라고도 합니다.

2. Attention 가중치

현재 쿼리(\(i\))에 대해 각 키(\(\leq i\))에 대한 Attention 가중치는 다음과 같이 얻어집니다.

• \(a_{i}^{l,h}\): 헤드 \(h\)의 위치 \(i\)에서의 Attention 가중치
• \(x_{i}^{l-1}\): 레이어 \(l-1\)에서의 위치 \(i\)의 입력 벡터
• \(W_{Q}^{l,h}\): 레이어 \(l\)의 헤드 \(h\)에 대한 쿼리(Query) 가중치 행렬
• \(W_{K}^{l,h}\): 레이어 \(l\)의 헤드 \(h\)에 대한 키(Key) 가중치 행렬
• \(d_k\): 스케일링 상수, 일반적으로 \(d_k = \sqrt{d_h}\)

\(W_{Q}^{l,h} \in \mathbb{R}^{d \times d_h}\)와 \(W_{K}^{l,h} \in \mathbb{R}^{d \times d_h}\)는 QK (query-key) 회로로 결합됩니다.

이 분해는 QK 및 OV 회로를 각각 잔류 스트림에서 읽고 쓰는 단위로 볼 수 있게 합니다.

3. Attention 블록 출력

Attention 블록의 출력은 개별 Attention 헤드의 합으로 구성되며, 이는 다시 잔류 스트림에 추가됩니다.

최종적으로 다음과 같이 표현됩니다.

• \(H\): Attention 헤드의 개수
• \(x_{i, \text{mid}, l}\): 레이어 \(l\)에서 위치 \(i\)의 중간 출력 벡터
• \(\text{Attn}_{l}(X_{\leq i}^{l-1})\): 레이어 \(l\)에서 위치 \(i\)까지의 입력 \(X_{\leq i}^{l-1}\)에 대한 Attention 결과의 합

이와 같은 Attention 메커니즘은 입력 데이터의 각 요소가 다른 모든 요소와의 관계를 고려하여 학습할 수 있도록 도와줍니다.

[[Check]]

계속 …