Reasoning | Weak-to-Strong Reasoning*

• Related Project: Private
• Category: Paper Review
• Date: 2024-07-18

Weak-to-Strong Reasoning

• url: https://arxiv.org/abs/2407.13647
• pdf: https://arxiv.org/pdf/2407.13647
• html: https://arxiv.org/html/2407.13647v1
• abstract: When large language models (LLMs) exceed human-level capabilities, it becomes increasingly challenging to provide full-scale and accurate supervisions for these models. weak-to-strong learning, which leverages a less capable model to unlock the latent abilities of a stronger model, proves valuable in this context. Yet, the efficacy of this approach for complex reasoning tasks is still untested. Furthermore, tackling reasoning tasks under the weak-to-strong setting currently lacks efficient methods to avoid blindly imitating the weak supervisor including its errors. In this paper, we introduce a progressive learning framework that enables the strong model to autonomously refine its training data, without requiring input from either a more advanced model or human-annotated data. This framework begins with supervised fine-tuning on a selective small but high-quality dataset, followed by preference optimization on contrastive samples identified by the strong model itself. Extensive experiments on the GSM8K and MATH datasets demonstrate that our method significantly enhances the reasoning capabilities of Llama2-70b using three separate weak models. This method is further validated in a forward-looking experimental setup, where Llama3-8b-instruct effectively supervises Llama3-70b on the highly challenging OlympicArena dataset. This work paves the way for a more scalable and sophisticated strategy to enhance AI reasoning powers. All relevant code and resources are available in url.

Contents

• Weak-to-Strong Reasoning
  • TL;DR

TL;DR

1. 대규모 언어모델의 슈퍼인텔리전스 달성을 위한 진보된 학습 패러다임 제안
2. Weak 모델을 이용한 Strong 모델의 인퍼런스 능력 향상 방법 연구
3. 선택적 파인튜닝과 선호도 최적화를 통한 복잡한 인퍼런스 과제 극복

1. 서론

인공 일반 지능(AGI)의 발전에 따라 휴먼의 인지 능력을 초월하는 모델을 개발하는 것은 필드 내의 주요 목표입니다. 이런 슈퍼인텔리전트 시스템의 개발은 AI 모델들을 위한 감독 및 학습 패러다임과 관련하여 많은 과제를 남겼습니다. 전통적인 학습 방법들은 이런 AI의 능력이 superviser의 능력을 초월함에 따라 부족해지게 되었습니다. 이 문제를 해결하기 위해, weak 모델만을 사용하고 strong 모델이 완전히 활용되지 않은 상태에서 수행할 수 있는 weak-to-strong 학습 패러다임을 탐구합니다.

이 연구에서는 “Weak 모델이 Strong 모델을 얼마나 효과적으로 지도할 수 있는가?”를 중심으로 복잡한 인퍼런스 과제에 적용할 weak-to-strong 학습 프레임워크의 가능성을 탐구합니다.

예비 연구들은 분류, 체스, 보상 모델링 과제에서 이 방법의 가능성을 입증했으나, 복잡한 인퍼런스 과제에서는 아직 밝혀지지 않았습니다. 인퍼런스은 휴먼의 인지 능력 중 중요한 측면을 대표하며, LLM이 세계를 이해하고 문제를 해결하는 데 있어 휴먼과 같은 능력을 모방하거나 초월할 수 있는지 평가하는 데 중요합니다.

2. 예비 사항

2.1 대규모 언어모델(LLM)의 전형적 학습 패러다임

• (1) General Supervised Fine-Tuning (SFT): 충분히 많은 양의 레이블이 포함된 훈련 데이터에 의존하지만, 고품질 데이터는 많은 레이블링 작업이 필요하며, 확장가능하지 않을 수 있습니다.
• (2) Distillation-Based Learning: 더 강한 모델(teacher model)이 피드백을 제공하여 대상 모델(student model)을 개선하는 데 도움을 주고, strong teacher 모델의 지식을 증류하는 것으로 볼 수 있습니다.
• (3) Self-Improvement Learning: 모델 스스로 생성한 정답을 확인하고 업데이트하며, 이는 바이너리 레이블 또는 세밀한 피드백 등을 사용하지만, 여전히 실제 정답(ground truth)이 필요하므로, SFT와 동일한 제약을 공유합니다.
• (4) Semi-Supervised Learning: 광범위한 레이블링 대신 소량의 고품질 시드 데이터셋에 의존합니다.

[일반적인 LLM 학습 과정 색인마킹]

2.2 weak-to-strong Reasoning Setup

이 섹션에서는 weak-to-strong reasoning에서의 인퍼런스 태스크를 다룹니다.

인퍼런스 과제는 기본적인 수학 문제의 해결을 요구하며, 각 단계는 이전 단계로부터 구축됩니다. 이런 과제는 단순 추측이 아닌 더 어려운 사고가 필요하므로, 모델의 학습 및 일반화 능력에 더 높은 기술을 요합니다.

먼저 weak 모델(Llama2-7b)을 사용해 strong 모델(Llama2-70b)의 인퍼런스 능력을 향상시키는 방법을 구현합니다. 즉, weak 모델을 이용하여 일부 문제 해결 능력을 갖도록 파인튜닝하고, strong 모델은 정답이나 인퍼런스 체인 없이 문제에만 접근할 수 있도록 구성합니다.

초기 단계에서는 실제 정답이 없을 경우에서의 잠재적으로 긍정적인 샘플(적절한 response를 반환한 샘플)을 식별합니다.

• 1단계에서 데이터의 일부만을 사용해 supervised learning을 수행합니다. 이후 strong 모델이 일정 수준의 인퍼런스 능력을 도달하면 다음 2단계로 넘어갑니다.
• 2단계에서 잠재적으로 부정적인 샘플을 포함한 전체 weak data를 활용하여, DPO Rafailov 등(2023)의 선호 학습 기반 접근 방식을 적용하여 strong 모델이 weak 모델의 오류에서 배우도록 유도합니다.

전체 프레임워크는 다음과 같습니다.

3. 실험 및 방법

• weak data에서 strong 모델로의 학습 전략 제안
• 양적 및 질적 성능 향상을 위한 이터레이티브 트레이닝 방법 도입
• 강화된 모델로 오류 방지 및 정확성 향상 구현

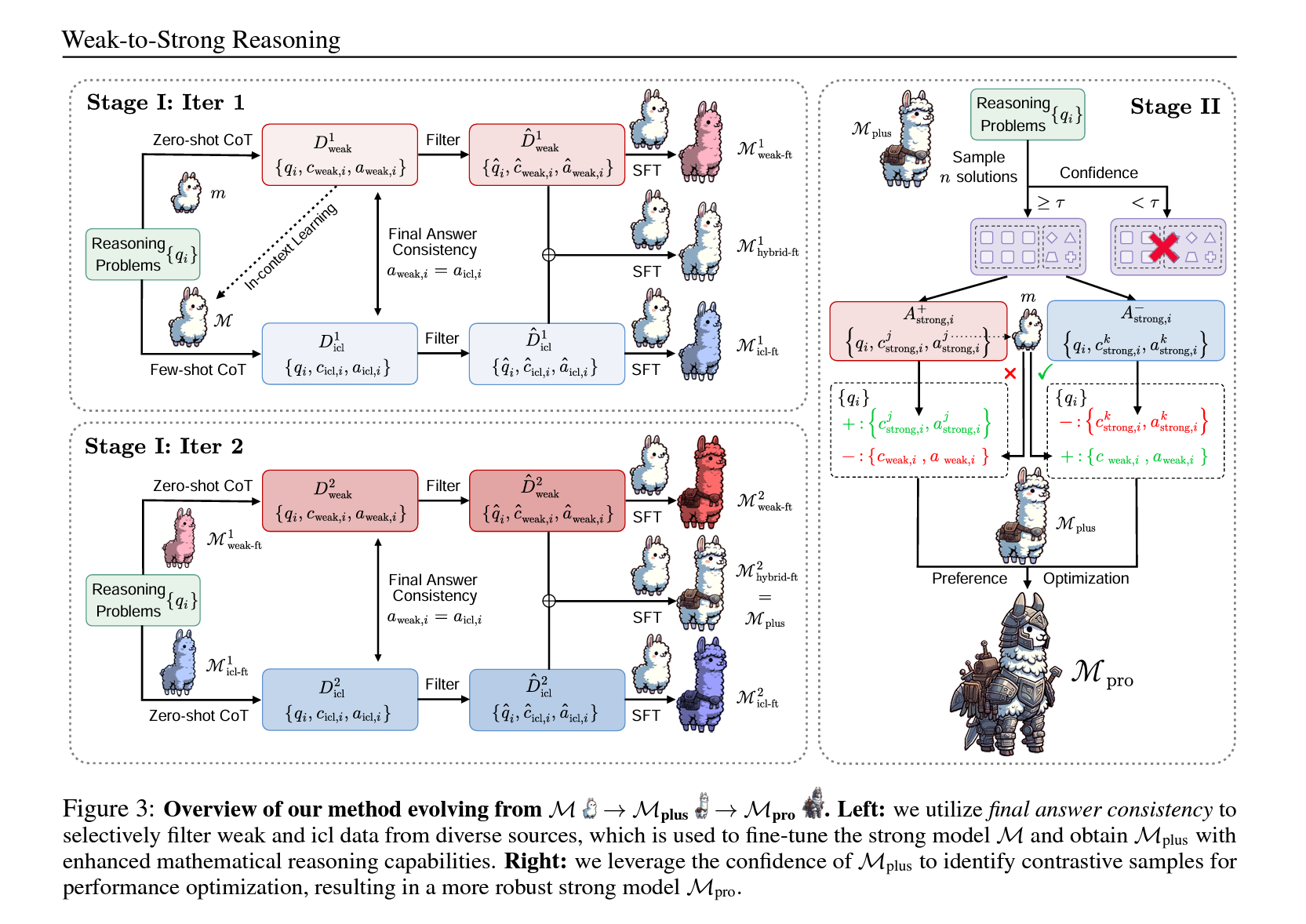
먼저 작은 양의 정확한 데이터를 사용하여 모델의 능력을 향상시키는 것이 유리하다는 가설을 설정합니다. 이를 위해, weak 모델에서 생성된 데이터와 strong 모델이 상황에 맞게 자체 생성한 데이터를 결합하여 선택적으로 데이터셋을 큐레이션하고 파인튜닝에 사용합니다.

두 번째 단계에서는 strong 모델의 개선된 인퍼런스 능력을 활용하여 선호도 최적화를 통해 학습을 진행합니다. 이 방법은 strong 모델이 weak 감독자의 오류에서 학습할 수 있게 하며, 금지 된 데이터셋과 같은 까다로운 시나리오에서 strong 모델의 기준보다 높은 성능을 달성할 수 있도록 합니다.

3.1 단계 I: “긍정적” 샘플에서 학습하기

weak 모델 \(m\)과 정답이 없는 수학 문제의 시리즈 \(\mathcal{Q}\)를 주어진 상태에서, \(m\)은 weak data \(\mathcal{D}_{\text{weak}} = \{q_i, c_{\text{weak}, i}, a_{\text{weak}, i}\}\) 를 생성합니다. \(q_i \in \mathcal{Q}\), \(c_{\text{weak}, i}\)는 인퍼런스 과정을 나타내며, \(a_{\text{weak}, i}\)는 최종 답을 나타냅니다. \(a_{\text{weak}, i}\)의 정확성은 알려져 있지 않습니다.

이 부분에서 중요한 챌린지는 “어떻게 \(m\)과 \(\mathcal{D}_{\text{weak}}\)을 최대한 활용하여 강력한 모델 \(\mathcal{M}\)의 수학적 인퍼런스 능력을 완전히 향상시키고 회복할 수 있을지”입니다.

이 단계에서는 weak data를 활용하여 강력한 모델 \(\mathcal{M}\)의 수학적 인퍼런스 능력을 키우는 방법에 집중합니다. 각 \(a_{\text{weak}, i}\)의 정확성이 불확실함에도 불구하고, 이 데이터를 통해 \(\mathcal{M}\)이 더 나은 인퍼런스 패턴을 학습할 수 있도록 지도하는 전략이 필요합니다. 이는 부분적으로 정답을 포함할 수도 있는 $\mathcal{D}_{\text{weak}}$의 정보를 최대한 활용하는 것을 의미합니다.

3.1.1 Weak data 전체로 파인튜닝

초기 전략은 strong 모델 $\mathcal{M}$을 weak dataset $\mathcal{D}_{\text{weak}}$ 전체에 걸쳐 파인튜닝하는 것입니다. 이전 연구(Burns 등, 2023)에서 이 접근 방식의 효과가 텍스트 분류 작업에서 검증되었으나, 인퍼런스 작업에서의 효과는 아직 탐색되지 않았습니다. 따라서, weak-to-strong 일반화 현상이 인퍼런스 능력을 향상시킬 수 있는지 여부를 조사하고 있습니다.

3.1.2 Weak In-Context Learning(이하 “ICL”)

또 다른 직관적인 접근 방식은 In-Context Learning(ICL, Dong 등, 2023b)입니다. 이 방법은 프롬프트에 몇 가지 훈련 샘플만을 데모로 요구합니다. 구체적으로는, $\mathcal{D}_{\text{weak}}$에서 무작위로 4개의 샘플을 데모로 선택하는데, 실제 정답에 접근할 수 없기 때문에 이 데모들이 증명이 가능할 정도로 정확한 지는 알 수 없습니다.

3.1.3 Weak-ICL 파인튜닝

• 문제 정의: weak 오류를 통한 Supervised learning에서 발생하는 문제들을 개선
• 해결 방법: weak data와 ICL data를 혼합하여 사용
• 선행 연구: Charikar et al., 2024; Lang et al., 2024

모델이 Supervised learning을 통해 weak 오류를 모방할 수 있다는 연구(Charikar et al., 2024; Lang et al., 2024)에 기초하여, 모든 데이터를 맹목적으로 사용하는 대신 사용 전에 weak data \(\mathcal{D}_{\text{weak}}\)을 정제하는 것을 제안합니다. 또한, 인-컨텍스트 학습을 통해 활성화된 강력한 모델의 내재된 능력을 활용하고자 합니다. 이 두 가지 아이디어에 기반하여, weak data \(\mathcal{D}_{\text{weak}}\)와 “ICL data”

를 사용하여 파인튜닝하는 Weak-ICL 파인튜닝을 도입합니다. \(q_i \in \mathcal{Q}\), \(c_{\text{ICL}, i}\) 및 \(a_{\text{ICL}, i}\)는 \(\mathcal{M}\)이 몇 번의 데모를 통해 생성한 것입니다.

[수학적 배경과 논리성]

Weak data \(\mathcal{D}_{\text{weak}}\)와 ICL data \(\mathcal{D}_{\text{ICL}}\) 모두에서 정확한 답변 여부를 결정할 수 없으나, 두 모델이 서로 다른 data 표현을 사용하면서 동일한 답변에 수렴하는 경우, 이는 정확성의 높은 가능성을 시사합니다. 이 현상은 다양한 방법 간의 일관성이 관찰될 때 결과의 신뢰성을 뒷받침합니다. 따라서 weak 모델과 강력한 모델이 각각 생성한 \(\mathcal{D}_{\text{weak}}\)과 \(\mathcal{D}_{\text{ICL}}\)을 비교하고, \(a_{\text{weak}, i} = a_{\text{ICL}, i}\)인 경우, 이후 Supervised learning을 위해 \(\mathcal{D}^{\text{weak}}\)과 \(\mathcal{D}^{\text{ICL}}\)을 선택합니다. 이 접근 방법을 최종 답변 일관성이라고 합니다.

[강화된 파인튜닝 모델 버전]

두 데이터셋의 조합을 고려할 때, 다음과 같은 세 가지 강화된 파인튜닝된 강력한 모델 버전을 얻을 수 있습니다.

• \(\mathcal{M}_{\text{weak-ft}}\): \(\mathcal{D}^{\text{weak}}\)에 파인튜닝된 \(\mathcal{M}\).
• \(\mathcal{M}_{\text{ICL-ft}}\): \(\mathcal{D}^{\text{ICL}}\)에 파인튜닝된 \(\mathcal{M}\).
• \(\mathcal{M}_{\text{hybrid-ft}}\): \(\mathcal{D}^{\text{weak}}\)과 \(\mathcal{D}^{\text{ICL}}\)의 합집합에 파인튜닝된 \(\mathcal{M}\).

이 방법을 통해, 두 데이터 소스의 통합을 통한 학습은 모델의 성능을 최적화하고, 다양한 시나리오에서의 유연성과 정확성을 향상시킬 가능성이 있고, 각 단계에서의 세심한 데이터 검증과 선택은 모델이 신뢰할 수 있는 결과를 생성하는 데 기여할 수 있습니다.

3.2 단계 II: “부정적” 샘플에서 학습하기

1단계에서 얻은 \(\mathcal{M}_{\text{hybrid-ft}}\)를 \(\mathcal{M}_{\text{plus}}\)로 명명하고, 이 모델은 추가적인 강화 가능성을 지니며, dual mathematical solutions을 학습하고, 다음으로, 원본 weak dataset \(\mathcal{D}_{\text{weak}} = \{q_i, c_{\text{weak}, i}, a_{\text{weak}, i}\}\) 에서 발생할 수 있는 잠재적 오류를 전략적으로 활용하는 선호 최적화 테크닉을 적용합니다. 이 방법은 강화된 모델이 유사한 오류를 미래 인퍼런스 과정에서 식별하고 피할 수 있도록 합니다. 학습을 위한 대조적 샘플 구성이 핵심 요소입니다.

• 문제 정의: 원본 weak dataset에서 발생할 수 있는 오류를 식별하고 피하는 전략 개발
• 해결 방법: 강화된 모델을 이용해 부정적 샘플로부터 학습

• 선행 연구: dual mathematical solutions을 학습한 강화된 모델 활용

• 예시

  • Question \(q_i\)

    Bob이 10명의 룸메이트가 있을 때, John은 Bob의 두 배보다 5명 더 많은 룸메이트를 갖고 있습니다. John은 몇 명의 룸메이트를 가지고 있습니까?

  • Weak Response \(\{c_{\text{weak}, i}, a_{\text{weak}, i}\}\)

    John은 10+5=15명의 룸메이트를 가집니다. 답은 15입니다.

  • Strong Response 1 \(\{c_{\text{strong}, i1}, a_{\text{strong}, i1}\}\)

    Bob은 10명의 룸메이트를 가집니다. Bob의 두 배는 2*10 = 20명입니다. John은 Bob의 두 배보다 5명 더 많으므로, John은 20+5 = 25명의 룸메이트를 가집니다. 답은 25입니다.

  • Strong Response 2 \(\{c_{\text{strong}, i2}, a_{\text{strong}, i2}\}\)

    Bob이 가진 룸메이트 수를 x라고 하면, John은 Bob의 두 배보다 5명 더 많은 룸메이트를 가집니다. 즉, John은 2x+5명의 룸메이트를 가집니다. Bob이 10명의 룸메이트를 가지므로, x=10입니다. John은 2*10+5 = 25명의 룸메이트를 가집니다. 답은 25입니다.

[신뢰도와 대조 샘플]

• 신뢰도 측정: 각 질문 \(q_i\)에 대해 \(\mathcal{M}_{\text{plus}}\)로부터 \(n\)개의 응답을 샘플링하고, 이 중 가장 자주 나타나는 답변의 확률을 신뢰도로 정의합니다. 신뢰도가 특정 임계값 \(\tau\) 이하로 떨어지면, 모델의 판단을 신뢰할 수 없다고 간주하고 해당 질문을 버립니다. 반대로, 신뢰도가 \(\tau\) 이상이면, 모델이 문제를 해결할 수 있다고 보고 대조 샘플을 구성합니다.
• 대조 샘플 구성: \(\mathcal{M}_{\text{plus}}\)가 확신하는 답변 \(a_{\text{strong}, i+}\)와 \(P(a_{\text{strong}, i+}) \geq \tau\)인 경우를 “정답”으로 간주합니다. 예를 들어, \(\tau = 0.6\)이고 10개의 샘플 응답 중 8개가 “4.2”라는 동일한 최종 답을 가진 경우, \(\mathcal{M}_{\text{plus}}\)는 이 문제의 정답이 “4.2”라고 간주합니다.
• \(n\)개의 샘플 응답을 두 집합으로 나눕니다. \(\mathcal{A}_{\text{strong}, i+}\)는 \(a_{\text{strong}, ij} = a_{\text{strong}, i+}\)인 경우, \(\mathcal{A}_{\text{strong}, i-}\)는 \(a_{\text{strong}, ik} \neq a_{\text{strong}, i+}\)인 경우입니다.

[모델 강화]

이 단계에서 \(\mathcal{M}_{\text{plus}}\)는 이런 샘플을 학습하여 정확하고 부정확한 해결책을 구분할 수 있게 되며, 이를 통해 더 강력한 모델 \(\mathcal{M}_{\text{pro}}\)로 발전합니다. 이 과정은 모델이 실수를 인식하고 피하는 능력을 개선하며, 더 정확한 인퍼런스를 가능하게 합니다.

4. 실험 결과

• GSM8K 및 MATH dataset: 첫 번째 단계에서 방법은 weak 모델의 감독만을 받았을 때 기존 방법보다 26.99포인트의 향상을 보였고, 선호도 최적화를 통해 추가적으로 8.49포인트의 성능 향상을 보였습니다..
• OlympicArena dataset: 이 까다로운 데이터셋에서도 두 단계 훈련 접근 방식이 기존 방법보다 3.19포인트 높은 성능을 보였습니다.