Anthropic - Toy Model Superposition*
- Related Project: Private
- Category: Paper Review
- Date: 2024-05-22
Towards Monosemanticity: Decomposing Language Models With Dictionary Learning
- url: https://transformer-circuits.pub/2022/toy_model/index.html#strategic-ways-out
- abstract: This paper explores the interpretability of neurons in artificial neural networks, particularly focusing on how neurons correspond to input features. While some neurons in studied models cleanly map to specific features, this is rare in large language models. Using toy models—small ReLU networks trained on synthetic data with sparse input features—we investigate the phenomenon of superposition, where models represent more features than dimensions, allowing compression at the cost of interference requiring nonlinear filtering. Our experiments show that with sparse features, models can store additional features in superposition, perform computations, and exhibit complex geometric structures. This suggests that real neural networks might simulate larger, highly sparse networks. We provide a direct demonstration that superposition occurs naturally in neural networks, offering a phase diagram for when and why this happens. Additionally, our findings hint at links between superposition, adversarial examples, and the performance of mixture of experts models. Our results reveal that superposition organizes features into geometric structures, demonstrating that neural networks exhibit these properties in specific regimes.
[포스트 원본에 코드 및 관련자료 多]
Contents
TL;DR
이 연구는 인공 신경망에서 특징의 Superpostion 현상을 수학적으로 분석하고, 이를 실험적으로 검증함으로써, 신경망이 특징을 표현하는 방식을 보다 깊이 이해하는 데 기여합니다. 또한, Superpostion은 네트워크의 정보 처리 및 저장 능력을 향상시킬 수 있는 잠재적인 메커니즘으로서 중요한 역할을 할 수 있음을 시사합니다.
- 인공 신경망의 특징 Superpostion 현상 탐구
- 토이 모델과 ReLU 네트워크를 사용한 실험적 검증
- 수학적 도구와 논리적 논증을 통한 현상 설명
[서론]
인공 신경망에서 각 뉴런이 입력의 해석 가능한 특징들과 정확히 대응되면 모델에 대한 해석이 용이해질 수 있으나 오랫동안 어려운 과제로 남아있습니다. 예를 들어, 이상적인 ImageNet 분류기에서는 각 뉴런이 특정 시각적 특징(e.g., 빨간색, 왼쪽 곡선, 개 코)의 존재에만 반응해야 하지만, 실제로는 특징들이 뉴런에 이렇게 깔끔하게 대응되지 않는 경우가 흔합니다.
이런 현상은 대규모 언어모델에서 더욱 두드러지는데, 뉴런들이 명확한 특징들과 완벽하게 대응되는 것을 찾는 것은 어렵습니다. 이로 인해 다음과 같은 질문이 제기됩니다.
왜 일부 모델과 작업에는 '깨끗하게 대응되는' 뉴런이 다수 존재하는가? 그렇다면 왜 다른 모델에는 이런 뉴런들이 드문가?
[이론적 배경 및 선행연구]
신경망의 특징이 Superpostion 현상을 통해 어떻게 표현될 수 있는지 이해하기 위해, Superpostion이란 개념을 도입하고 이를 수학적으로 모델링합니다. Superpostion은 특징이 희소할 때, 선형 모델이 수행할 수 있는 것 이상으로 압축을 허용하지만 ‘간섭’이 발생하며, 이는 비선형 필터링을 필요로 합니다.
[참고: 선행 연구와의 비교]
- 압축 감지(Compressed Sensing): 수학에서 오랜 기간 동안 연구된 주제로, Superpostion과 밀접한 관련이 있습니다.
- 분산, 밀집, 인구 코드(Distributed, Dense, and Population Codes): 신경과학과 딥러닝에서 특징의 Superpostion을 설명하는 데 사용된 개념입니다.
[자연어 처리에서의 Sparsity]
- 희소성(sparsity)은 입력 데이터나 feature(feature)들이 대부분 0이거나 무의미한 값을 가지는 경우를 의미합니다. 예를 들어, 텍스트 데이터를 토크나이징한 후 특정 단어들이 문서에 나타날 때 0이 아닌 값으로 나타나고, 나타나지 않을 때 0으로 나타나는 것처럼, 데이터의 대부분이 0인 경우를 말합니다.
- 이 논문에서는 합성 데이터를 사용한 작은 모델을 사용해서 작은 ReLU 네트워크를 사용하여 희소한 입력 feature을 통해 모델이 어떻게 더 많은 feature을 표현하는지 실험을 수행하고, 설명을 위해 중첩(superposition)과 간섭(interference)이라는 개념을 사용합니다.
- 중첩(superposition)은 모델이 차원의 수보다 더 많은 feature을 표현할 수 있는 현상을 의미하며, 희소한 feature만 존재해도 중첩을 통해 모델이 선형 모델보다 더 많은 feature을 압축할 수 있지만, 이로 인해 간섭이 발생하며 간섭을 제어하기 위해 비선형 필터를 사용합니다.
평균 제곱 오차(MSE, Mean Squared Error) 손실에 대한 스칼라 승수는 다음과 같이 표현됩니다.
\[\text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2\]위 평균 제곱 오차(MSE) 수식에서
- $N$은 데이터 포인트의 수
- $y_i$는 실제 값
- $\hat{y}_i$는 예측 값
중요도에 따라 특정 feature의 손실에 가중치를 부여하여 표현합니다.
\[\text{Weighted MSE} = \frac{1}{N} \sum_{i=1}^{N} w_i (y_i - \hat{y}_i)^2\]위 수식에서 $w_i$는 각 데이터 포인트 $i$에 대한 중요도를 나타내는 스칼라 승수이며, 특정 feature $x_j$의 중요도에 따른 손실은 다음과 같습니다.
\[\text{Weighted MSE} = \frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{d} \alpha_j (y_{i,j} - \hat{y}_{i,j})^2\]- $d$는 feature의 수
- $\alpha_j$는 feature $j$에 대한 중요도를 나타내는 스칼라 승수
- $y_{i,j}$는 데이터 포인트 $i$의 실제 값에서 feature $j$의 값
- $\hat{y}_{i,j}$는 데이터 포인트 $i$의 예측 값에서 feature $j$의 값
스칼라 승수를 통해 모델은 특정 feature에 더 높은 중요도를 부여하여, 해당 feature이 예측 성능에 더 큰 영향을 미치도록 할 수 있습니다.
2차원에서는 후속 작업을 위해 ReLU를 추가하고, feature의 sparsity를 수정하여 표시합니다.
Dense feature를 사용하면 모델은 가장 중요한 두 가지 특성(주성분 분석이 제공할 수 있는 것과 비슷하게)의 직교 기반을 표현하는 방법을 학습하고 나머지 세 가지 특성은 표현되지 않습니다. 그러나 feature를 sparse하게 만들면 다음 Figure과 같이 표현할 수 있습니다.
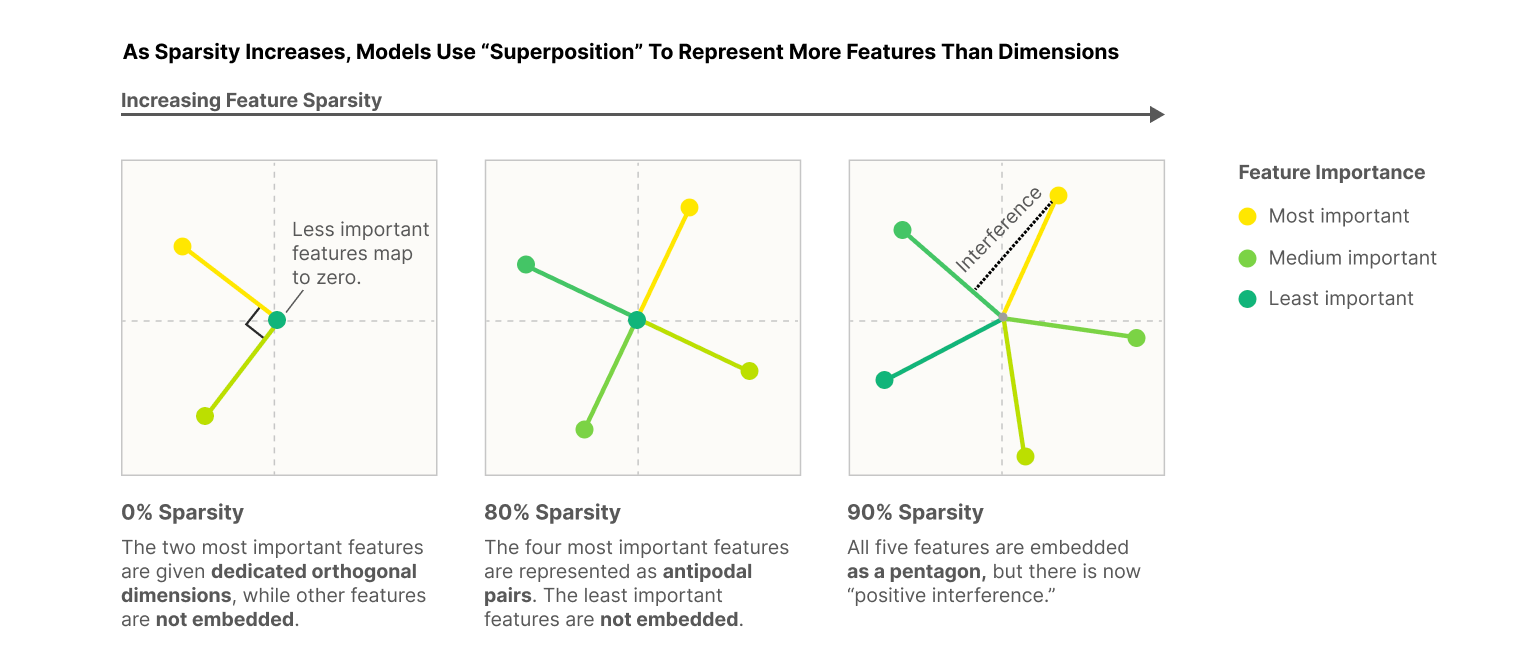
- 0% sparsity: 2가지 중요한 feature을 직교 기저로 표현하며, 나머지 feature은 무시
- 80% sparsity: 4가지 중요한 feature이 대칭적으로 표현되고, 덜 중요한 한 가지 feature은 무시
- 90% sparsity: 5가지 모든 feature이 표현되지만, 간섭이 발생하여 상호작용하게 되므로, 더 많은 정보를 표현
Sparsity이 높을수록 모델은 더 많은 중요한 feature을 표현하게 되며, 간섭을 통해 더 많은 정보를 압축할 수 있는 것이라는 개념을 설명합니다.
이 논문은 기존 이론들을 중첩과 간섭이라는 개념으로 설명하며, sparsity은 모델이 입력 데이터의 중요한 feature을 얼마나 압축하여 표현할 수 있는지를 이해하기 위해 다양한 탐구를 수행합니다.
[방법]
위의 이론들을 이해하기 위해 중요한 feature의 수를 모델의 평균 제곱 오차 손실에 대한 스칼라 승수로 확인합니다.
데이터셋 및 실험 설정: 토이 모델을 사용하여 희소한 입력 특징을 가진 작은 ReLU 네트워크를 학습시킵니다. 수식에서는 다섯 가지 특징을 두 차원으로 임베딩하고 ReLU를 이용한 필터링 후의 결과를 분석합니다.
-
수식 정의:
\[\text{ReLU}(x) = \max(0, x)\] \[\text{Embedding representation}: h = Wx + b\]수식에서 $W$는 가중치 행렬, $x$는 입력 벡터, $b$는 바이어스 벡터입니다.
-
모델 학습 및 평가:
- Sparsity가 증가함에 따라 특징들이 어떻게 추가적으로 저장되는지 관찰합니다.
- Superpostion을 통해 모델이 계산을 수행할 수 있는지를 특정 케이스에서 실험적으로 보여줍니다.
[참고자료 1] 인공 신경망에서의 특징 Superpostion 현상에 대한 수학적 분석
1. 문제 정의
신경망에서 각 뉴런이 입력의 특징을 어떻게 표현하는지는 모델의 해석성과 성능에 중요한 영향을 미칩니다. 특징 Superpostion은 다차원 입력 공간에서 특징이 뉴런의 활성화 공간으로 어떻게 매핑되는지를 설명하는 데 사용됩니다. 이 연구의 목적은 특징 Superpostion이 모델의 정보 처리 능력에 미치는 영향을 수학적으로 분석하는 것입니다.
2. Superpostion 모델의 수학적 정의
Superpostion은 고차원의 특징을 저차원의 뉴런 활성화 공간에 표현할 때, 여러 특징들이 하나의 뉴런에 매핑되어 정보가 중첩되는 현상을 말합니다. 수학적으로는 다음과 같이 모델링할 수 있습니다.
\[h = \text{ReLU}(Wx + b)\]수식에서 \(x \in \mathbb{R}^n\)는 입력 벡터, \(W \in \mathbb{R}^{m \times n}\)는 가중치 행렬, \(b \in \mathbb{R}^m\)는 바이어스 벡터, \(h \in \mathbb{R}^m\)은 활성화 벡터입니다. ReLU 함수는 비선형성을 추가하여 간섭 효과를 관리합니다.
3. Superpostion의 수학적 특성 및 결과
가. 선형 대수적 접근
Superpostion 현상은 선형 대수학적으로 설명할 때, 입력 벡터 \(x\)의 각 차원이 활성화 벡터 \(h\)의 차원보다 많을 경우에 관찰됩니다. 이때 \(W\) 행렬은 고차원을 저차원으로 투영하는 역할을 하며, 이 과정에서 다수의 입력 특징이 하나의 출력 차원에 매핑되어 Superpostion을 일으킵니다.
나. 정보 압축 및 간섭
정보의 압축은 Superpostion을 통해 실현됩니다. 각 입력 특징은 저차원의 활성화 공간에서 ‘거의 직교적(almost orthogonal)’ 상태로 표현될 수 있습니다. 그러나, 완벽하게 직교하지 않기 때문에 서로 간에 약간의 간섭이 발생할 수 있습니다. 이는 다음과 같은 식으로 표현할 수 있습니다.
\[W^TW \approx \text{Diag}\lambda_1, \lambda_2, ..., \lambda_m)\]수식에서 \(\lambda_i\)는 \(i\)번째 뉴런의 특징에 대한 ‘중요도’를 나타내는 값입니다. 완벽한 직교성이 없기 때문에 Superpostion은 모델의 학습 동안 특징 간 간섭을 최소화하는 방향으로 가중치를 조정합니다.
다. 비선형 필터링의 역할
ReLU 함수의 도입은 비선형 필터링을 통해 간섭을 관리하는 중요한 메커니즘입니다. ReLU는 음수 값을 제거함으로써 활성화 공간에서의 간섭 효과를 줄이고, 모델이 더 명확하게 특징을 구분하도록 돕습니다.
4. 결론 및 논의
이 연구는 인공 신경망에서 특징 Superpostion 현상을 수학적으로 정의하고 분석하였습니다. 수학적 도구와 모델을 통해 신경망이 어떻게 고차원의 정보를 효과적으로 저차원의 뉴런 활성화 공간에 압축하는지를 설명하였습니다. 이런 이해는 신경망의 구조와 기능을 최적화하는데 중요한 기초 자료를 제공합니다.
실험을 통해 희소 특징이 있는 경우, Superpostion을 통해 더 많은 특징을 저장할 수 있음을 확인했습니다. 이런 결과는 비선형 활성화 함수가 모델의 학습 및 표현 능력에 어떻게 기여하는지를 보여줍니다.
5. 논리적 귀결
- 특징의 희소성: 특징이 희소할수록 Superpostion은 더 유리하며, 이는 네트워크가 더 많은 정보를 압축하여 저장할 수 있게 합니다.
- 간섭 및 비선형 필터링: Superpostion은 특징 간 간섭을 유발할 수 있으며, 이는 ReLU와 같은 비선형 필터를 통해 해결할 수 있습니다.