PO | Discovering PO Algorithms*
- Related Project: Private
- Category: Paper Review
- Date: 2024-06-11
Discovering Preference Optimization Algorithms with and for Large Language Models
- url: https://arxiv.org/abs/2406.08414
- pdf: https://arxiv.org/pdf/2406.08414
- html https://arxiv.org/html/2406.08414v1
- abstract: Offline preference optimization is a key method for enhancing and controlling the quality of Large Language Model (LLM) outputs. Typically, preference optimization is approached as an offline supervised learning task using manually-crafted convex loss functions. While these methods are based on theoretical insights, they are inherently constrained by human creativity, so the large search space of possible loss functions remains under explored. We address this by performing LLM-driven objective discovery to automatically discover new state-of-the-art preference optimization algorithms without (expert) human intervention. Specifically, we iteratively prompt an LLM to propose and implement new preference optimization loss functions based on previously-evaluated performance metrics. This process leads to the discovery of previously-unknown and performant preference optimization algorithms. The best performing of these we call Discovered Preference Optimization (DiscoPOP), a novel algorithm that adaptively blends logistic and exponential losses. Experiments demonstrate the state-of-the-art performance of DiscoPOP and its successful transfer to held-out tasks.
Contents
- Discovering Preference Optimization Algorithms with and for Large Language Models
TL;DR
- 대규모 언어모델 자동 선호 최적화 알고리즘 발견: 언어 모델을 활용한 선호 최적화 알고리즘의 자동 발견 및 평가
- DiscoPOP 알고리즘 개발 및 검증: 고성능 선호 최적화 알고리즘인 DiscoPOP 개발 및 다양한 벤치마크에서의 성능 검증
- 수학적 접근과 메타 최적화: 강화된 수학적 모델과 메타 최적화를 통한 알고리즘 발견 과정 설명
1 서론
언어 모델(Large Language Models, LLMs)의 훈련은 대규모 텍스트 코퍼스에서 사전 훈련된 모델을 시작으로, 이를 휴먼의 선호에 맞게 파인튜닝하는 과정을 포함한다. 사전 훈련된 모델은 때로 해로운, 위험한, 비윤리적인 완성을 생성할 수 있는데, 이를 완화하기 위해 선호도 순위가 매겨진 완성 데이터를 통해 휴먼의 가치와 일치시키려는 시도가 있다. 이 접근 방식은 휴먼의 피드백에 따른 강화학습(RLHF)으로 대중화되었으며, 최근에는 오프라인 선호 최적화 알고리즘으로 문제를 지도 학습(Supervised learning) 목표로 캐스팅한 직접 선호 최적화(DPO)와 시퀀스 우도 보정(SLiC) 등이 개발되었다. 각기 다른 태스크에서 좋은 성능을 내는 알고리즘이 존재하는지 여부는 여전히 개방된 질문이다.
2 배경
선호 최적화
사전 훈련된 언어 모델 정책 $\pi_\theta$와 데이터셋 $N$을 고려해보자. 이 데이터셋은 프롬프트 $x$와 선호 순위가 매겨진 완성 $y_w$ 및 $y_l$로 구성된다. $y_w \succ y_l$는 휴먼 평가자가 $y_w$를 $y_l$보다 선호한다는 것을 나타낸다. 이 작업은 $\pi_\theta$를 이런 선호에 내재된 휴먼의 가치와 일치시키는 것이다. 이는 일반적으로 두 단계로 진행된다.
- 기초 모델 제안
- 확장/업데이트
- 맥락 및 적합성
- 내부 루프 최적화 실행
- 제안된 목표의 내부 루프 평가
- LLM 주도 발견
- 발견된 정책 최적화(DiscoPOP)
먼저, 파라미터화된 보상 모델 $r_\phi$을 학습하는 보상 모델링 단계가 있다. 브래들리-테리 모델을 가정할 때, 데이터의 확률은 다음과 같이 표현될 수 있다.
\[P(y_w \succ y_l) = \frac{\exp(r_\phi(y_w, x))}{\exp(r_\phi(y_w, x)) + \exp(r_\phi(y_l, x))}\]그리고 이는 최대 우도 원리를 통해 $\phi$에 대해 간단히 최적화될 수 있다. 정책 최적화의 두 번째 단계에서는 언어 모델을 학습된 보상과 대조하여 강화학습 알고리즘을 사용한다. 일반적으로, 모델과 사전 RL 참조 정책 $\pi_{\text{ref}}$ 사이에 KL 패널티가 도입된다.
\[\max_{\pi_\theta} \mathbb{E}_{y \sim \pi_\theta, x \sim P} [r_\phi(y, x)] - \beta \text{KL}(\pi_\theta, \pi_{\text{ref}})\]이 과정을 단순화하기 위해, DPO는 보상 모델링 및 온라인 RL 절차를 생략하고, KL 항을 분해하여 문제를 엔트로피-규제된 RL 밴딧 작업으로 표현한다. 이를 위한 알려진 분석적 해는 다음과 같다.
\[\pi^*(y | x) = \frac{Z(x)^{-1} \exp(\beta^{-1}r_\phi(y, x))}{\pi_{\text{ref}}(y | x)}\]바이너리 분류 문제로 작업을 표현하기 위해, 보상 차이를 기반으로 다음과 같이 정의한다.
\[\min_{\pi_\theta} \log \left[ \beta(\pi_\theta(y_w \\| x) - r_\phi(y_w, x) - \pi_\theta(yl \\| x) + r_\phi(yl, x)) \right]\]로그 비율 차이 $\rho = \log \frac{\pi_\theta(y_w \| x)}{\pi_{\text{ref}}(yl \| x)}$로 정의된다. DPO에서, 함수 $f = \log \sigma$는 BT 모델 가정에 따른 시그모이드 함수의 음의 로그로 파생된다.
3 LLM 주도 목표 발견
적절한 목표 함수를 선택하는 것은 네트워크에 기능을 부여하는 데 중요하다. 여기에서는 LLM 코드 수준 목표 함수 제안을 통한 발견 과정을 자세히 설명한다.
초기 맥락 구축. 초기 시스템 프롬프트에서, 여러 확인된 목표 함수들을 코드와 그에 해당하는 성능과 함께 ‘burn-in’한다. 또한 문제 세부사항 및 출력 응답 형식의 예를 JSON 사전으로 제공한다.
LLM 조회, 구문 분석 및 출력 유효성 검사. LLM을 조회하고, 응답 JSON을 구문 분석하며, 훈련 실행을 시작하기 전에 일련의 단위 테스트(e.g., 유효한 출력 형태 확인)를 실행한다. 구문 분석 또는 단위 테스트에 실패하면, 오류 메시지를 피드백으로 제공하면서 새로운 솔루션을 다시 샘플링한다.
성능 평가. 제안된 목표 함수는 미리 정의된 downstream 검증 작업을 최적화하는 능력을 기준으로 평가된다. 결과 성능 지표를 η라고 한다.
반복적 개선. 성능 제공을 피드백으로 사용하여, LLM은 반복적으로 제안을 개선한다. 각 반복에서, 모델은 새로운 후보 손실 함수를 합성하며, 이전에 성공적이었던 공식의 변형과 기존 벤치마크를 개선할 수 있는 완전히 새로운 공식을 모두 탐색한다. 이 반복
과정은 최적의 손실 함수 집합이 관찰될 때까지 또는 최대 세대에 도달할 때까지 반복된다.
이런 일반적인 목표 발견 과정을 Figure 1과 알고리즘 1에서 요약한다.
[알고리즘 1 LLM 주도 목표 발견]
\[\begin{align*} 1:& \text{Initialize LLM with verified loss function } L_0 \text{ and its performance } \eta_0 \\ 2:& \text{For each generation } i = 1, 2, \ldots, N \text{ do:} \\ 3:& \quad \text{LLM proposes new candidate objective function } f_i \\ 4:& \quad \text{Execute unit tests to verify candidate validity and resample if necessary} \\ 5:& \quad \text{Evaluate objective function using performance metric } \eta_i = \text{Eval}(f_i) \\ 6:& \quad \text{Update LLM context with performance data: } C_i = C_{i-1} \cup \{(f_i, \eta_i)\} \\ 7:& \quad \text{LLM improves generation strategy based on feedback} \\ 8:& \text{Until convergence criterion is met or maximum generations reached} \end{align*}\] \[\begin{align*} 1:& \text{LLM을 확인된 손실 함수와 그 성능으로 초기화.} \\ 2:& \text{각 세대 } i \text{에 대해 반복} \\ 3:& \quad \text{LLM이 새로운 후보 목표 함수 } f_i \text{를 제안} \\ 4:& \quad \text{후보의 유효성을 확인하고 필요한 경우 다시 샘플링하기 위해 단위 테스트를 실행.} \\ 5:& \quad \text{성능 지표 } \eta \text{를 사용하여 목표 함수 평가} \\ 6:& \quad \text{성능 데이터로 LLM 맥락 업데이트} \\ 7:& \quad \text{피드백을 바탕으로 LLM이 생성 전략을 개선} \\ 8:& \text{수렴 기준이 충족되거나 최대 세대에 도달할 때까지} \end{align*}\]4 오프라인 선호 최적화 목표 발견
4.1 다중 턴 대화 발견 과제 - MT-Bench
이 섹션에서는 LLM을 활용하여 자동으로 새로운 최신 선호 최적화 알고리즘을 생성한다. 각 생성된 유효한 목표 함수 \(f_i\)에 대해, LLM을 파인튜닝한 후 성능 평가 점수를 수집한다. 구체적으로 ‘alignment-handbook’ 저장소를 기반으로 모델을 파인튜닝한다. 이 저장소를 사용하여 DPO로 ‘Zephyr 7B Gemma’를 재현하며, 이 모델은 MT-Bench에서 7B 모델에 대한 최고 점수를 달성했다. 새로운 목표 함수 평가 시 DPO를 해당 생성된 목표 함수로 대체하고, 동일한 하이퍼파라미터를 유지한다.
각 목표 함수는 입력으로 받는다.
- \(x\), \(\log \pi_{\text{ref}}(y_w \\| x)\)
- \(x\), \(\log \pi_{\text{ref}}(y_l \\| x)\)
- $ x $
4.2 발견 결과
약 100개의 목표 함수를 평가한 후, 가장 성능이 좋은 함수들을 기록했다. 여기서는 각 발견된 목표 함수에 대한 세부 정보를 제공하며, 전체 목표 손실 함수와 해당 코드는 Appendix E에 제공된다. 또한, MT-Bench에서 가장 잘 수행된 서브 태스크 평가를 Figure 4에 표시한다.
5 보류된 평가
테이블 1에 나열된 발견된 각 목표 함수를 보류된 작업에서 검증한다. 특히 PADLL과 LRML은 일관되게 잘 수행된다. 이런 함수들은 Alpaca Eval 2.0에서 높은 승률을 보이며, 일부는 기존 손실 함수를 능가한다.
5.1 단일 턴 대화 - Alpaca Eval 2.0
GPT-4를 사용하여 훈련된 LLM 정책의 완성도를 평가하고, SFT 기본 모델과 비교한다. 이 평가는 20K 휴먼 주석과 검증되었으며, 길이 편향을 줄이는 것을 목표로 한다.
5.2 요약 (TL;DR)
Reddit 포럼 게시물을 주어진 요약 \(y\)를 생성하도록 LLM 정책을 훈련시킨다. ‘zephyr-7b-gemma-sft’를 사용하여 Reddit TL;DR 요약 선호 데이터셋의 10%를 기준으로 각 기준 및 발견된 목표 함수로 파인튜닝한다. 요약의 품질을 평가하기 위해 Alpaca Eval 2.0 라이브러리와 사용자 정의 평가 데이터셋을 사용한다.
6 DiscoPOP 분석
LRML(DiscoPOP)은 보류된 평가 작업에서 일관되게 높은 성능을 보여줍니다. 이 섹션에서는 LRML을 자세히 분석하고, 기존 최고의 목표보다 어떻게 우수한 성능을 발휘하는지 직관적으로 설명한다.
6.1 로그 비율 조절 손실 (DiscoPOP)
로그 비율 조절 손실은 로지스틱 손실(e.g., DPO에서 사용됨)과 지수 손실의 동적 가중치 합이다. 각 가중치는 로그 비율의 차이(\(\rho\))에 대한 시그모이드 계산을 통해 결정된다.
\[f_{\text{lrml}}(\beta \rho) = (1 - \sigma(\rho/\tau)) f_{\text{dpo}}(\beta \rho) + \sigma(\rho/\tau) \log(1 + \exp(\beta \rho))\]6.2 DiscoPOP의 한계
단일 턴 텍스트 생성과 텍스트 요약에서 잘 수행되지만, LRML은 \(\beta\) 값이 너무 낮거나 높을 때 수렴에 어려움을 겪는다. 이는 \(\beta\)가 발견 과정에서 본 적이 없거나 사용되지 않았기 때문일 가능성이 있다.
7 관련 연구
7.1 대규모 언어모델을 이용한 진화 및 탐색
대규모 언어모델(LLMs)은 자연어로 제시된 문제에 대한 다수의 후보 솔루션을 빠르고 자동적으로 생성할 수 있는 강력한 도구이다. 이런 모델들은 진화적 메타 발견과 같은 인구 기반 검색 절차를 주도하는 데 효과적이다. 최근에는 코딩 문제, 신경 아키텍처 검색, 가상 로봇 디자인 설정, 보상 함수 등 다양한 분야에서 이 접근 방식을 적용한 연구가 있다. 또한, LLM은 블랙박스 최적화를 위한 진화 전략과 품질-다양성 접근 방식을 위한 재조합 연산자로서의 역할을 수행할 수 있음이 최근에 밝혀졌다.
7.2 머신러닝을 위한 자동 발견
머신러닝 알고리즘의 자동 발견을 위한 접근 방법은 다양하다. 일부 이전 연구는 유전 알고리즘을 사용하여 강화 학습 알고리즘, 호기심 알고리즘, optimizer 등을 위한 특정 도메인 언어를 이용해 ML 함수의 공간을 탐색한다. 다른 연구에서는 신경망을 이용해 전이 가능한 목표 함수를 파라미터화하고 진화 전략으로 최적화한다.
7.3 선호 최적화 알고리즘
DPO와 같은 지도 학습(Supervised learning)으로의 감소는 사용하기 쉽게 만들지만, 다른 접근 방식은 REINFORCE의 변형 사용, 단계별 선호를 통한 더 세밀한 피드백 제공, 보상 재분배 등을 통해 RL 단계를 단순화하려고 한다. 또한, 정책 모델에서 샘플링과 자체 선호 순위 획득을 교차하여 반복적인 오프라인 훈련을 사용하는 방법도 있다.
8 결론
본 논문에서는 LLM 주도 목표 발견을 제안하고 사용하여 새로운 오프라인 선호 최적화 알고리즘을 생성하였다. 구체적으로, 보류된 평가 작업에서 강력한 성능을 보이는 선호 최적화 손실을 발견할 수 있었다. 가장 높은 성능을 보인 손실은 로지스틱 손실과 지수 손실의 혼합이며, 비볼록 형태일 수도 있음을 새로운 통찰로 제시한다.
한계 및 향후 연구
현재 접근 방식의 몇 가지 한계가 있다.
첫째, LLM 목표 제안을 가장 효과적으로 생성하는 방법에 대한 탐구는 초기 단계에 불과하다. 초기 탐색 실험에서 온도 샘플링이나 성능 정렬을 사용해도 유의미한 개선이 이루어지지 않았다. 훈련 실행에 대한 더 많은 정보를 활용하거나 명령 프롬프트 템플릿을 자동으로 조정하는 것을 상상할 수 있다.
둘째, 가장 높은 성능을 보인 손실은 베타를 전통적인 의미에서 재사용하여 모델의 기능적 행동과 KL 페널티에 영향을 미쳤다. 이는 향후 다양한 형태를 연구하고, 각각을 별도로 조정할 수 있는 여러 부동 소수점 파라미터를 포함하는 형태를 연구하는 것을 동기 부여한다. 이 단일 파라미터에 대한 초기 분석을 제공하고 일부 인스턴스에서 함수적 행동이 모델 훈련의 불안정성을 초래하는 것을 관찰했다. 더 많은 파라미터 분석과 목표의 재구성이 향후 연구에 도움이 될 것이다.
마지막으로, 본 연구는 비공개 모델(GPT-4)을 사용하여 코드를 생성하므로 재현성이 제한되고 비용이 많이들기 때문에, 향후 연구는 생성된 모델 자체를 사용하여 코드를 생성할 수 있다.
보다 넓은 영향 및 윤리적 고려
이 논문은 더 나은 성능의 새로운 오프라인 선호 최적화 알고리즘을 생성하기 위해 사용되는 LLM 주도 발견 인컨텍스트 학습 파이프라인을 제시한다. 그러나 이 파이프라인이 도구로서 잘못 사용되거나 LLM이 바람직하지 않거나 비윤리적이거나 해로운 출력을 생성하도록 훈련될 수 있다. 또한, LLM과 LLM의 훈련으로 인해 출력이 환각에 취약해지므로, LLM의 모든 출력에 콘텐츠 필터를 적용하는 것이 중요하다. 마지막으로, 이 작업은 언어 모델에서 코드 수준 자기 개선으로 향하는 작은 단계를 나타내며, 이는 의도하지 않은 행동을 초래할 수 있다.
1 Introduction
Training Large Language Models (LLMs) usually involves starting with a model pre-trained on large text corpora and then fine-tuning it to match human preferences. Pre-trained, and even instruction fine-tuned LLMs, can generate harmful, dangerous, and unethical completions [Carlini et al., 2021, Gehman et al., 2020]. To mitigate this and align an LLM with human values, we use human preference alignment through preference-ranked completion data. This approach has become an industry standard, popularized by reinforcement learning with human feedback (RLHF) [Christiano et al., 2017, RLHF], and more recently, by offline preference optimization algorithms like direct preference optimization [Rafailov et al., 2023, DPO] and sequence likelihood calibration [Zhao et al., 2023, SLiC], which cast the problem as a supervised learning objective. Many algorithms have been proposed in the literature for offline preference optimization, and it remains an open question which one performs best across tasks. While a strictly dominant algorithm may not exist, some algorithms likely exhibit generally improved performance. To date, all existing state-of-the-art preference optimization algorithms [Rafailov et al., 2023, Azar et al., 2023, Zhao et al., 2023] have been developed by human experts. Despite their advancements, these solutions are inherently constrained by human limitations, including creativity, ingenuity, and expert knowledge.
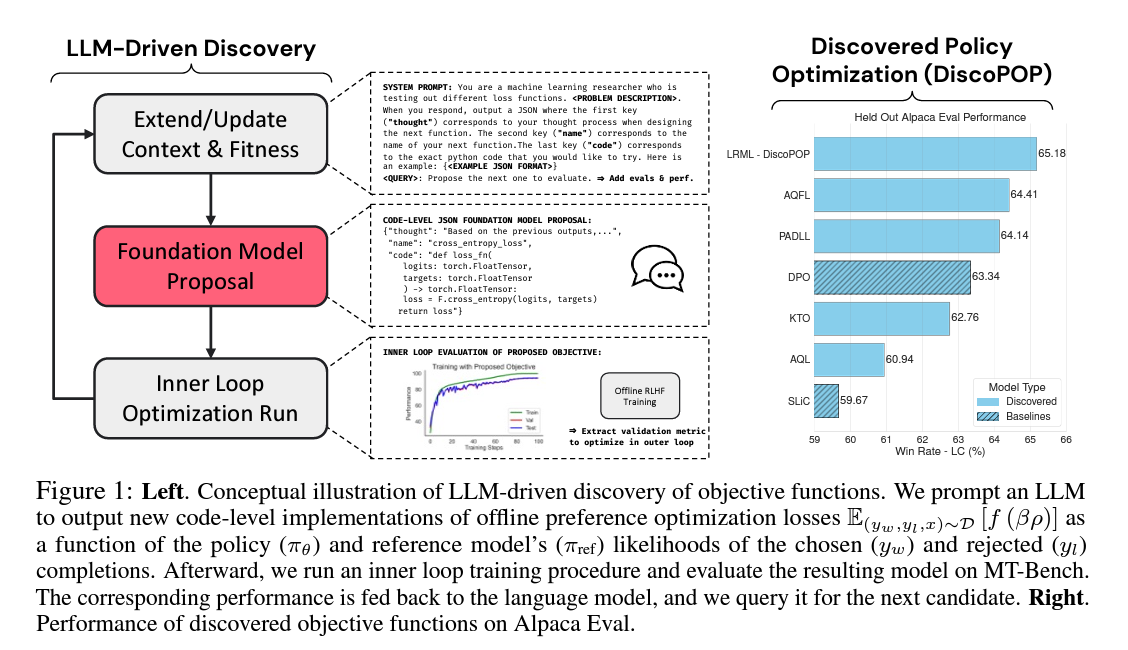
Figure 1: Left. Conceptual illustration of LLM-driven discovery of objective functions. We prompt an LLM to output new code-level implementations of offline preference optimization losses E(yw ,yl,x)∼D [f (βρ)] as a function of the policy (πθ) and reference model’s (πref) likelihoods of the chosen (yw) and rejected (yl) completions. Afterward, we run an inner loop training procedure and evaluate the resulting model on MT-Bench. The corresponding performance is fed back to the language model, and we query it for the next candidate. Right. Performance of discovered objective functions on Alpaca Eval.
In this work, we aim to address these limitations by performing LLM-driven discovery in order to automatically generate new state-of-the-art preference optimization algorithms without continual expert human intervention in the development process. While previous works [Ma et al., 2023, Yu et al., 2023] have used LLMs to design environment-specific RL reward functions, we discover general purpose objective functions which can be used across various preference optimization tasks. More specifically, we iteratively prompt an LLM to propose new preference optimization loss functions and evaluate them, with the previously proposed loss functions and their task performance metric (in our case, MT-Bench scores [Zheng et al., 2024]) as in-context examples. After performing this automatic discovery process, we catalog high-performing loss functions and introduce a particularly strong one we call Discovered Preference Optimization (DiscoPOP), a new algorithm. To ensure robustness beyond MT-Bench, we validate DiscoPOP using AlapacaEval 2.0 [Dubois et al., 2024], showing an improvement in win rates against GPT-4 from DPO (11.23% 13.21%). Additionally, in separate, held-out, tasks such as summarization and controlled generation, models trained with the DiscoPOP loss outperform or perform competitively with existing preference optimization algorithms.
Contributions:
- We propose an LLM-driven objective discovery pipeline to discover novel ⃝ offline preference optimization algorithms (Section 3).
- We discover multiple high-performing ⃝ preference optimization losses. One such loss, which we call Discovered Preference Optimization (DiscoPOP), achieves strong performance across multiple held-out evaluation tasks of multi-turn dialogue (AlpacaEval 2.0), controlled sentiment generation (IMDb) and summarization (TL;DR) tasks.
- We provide an initial analysis of DiscoPOP, which is a weighted sum of logistic and ⃝ exponential losses, and discover surprising features. For example, DiscoPOP is non-convex.
2 Background
Preference Optimization
Consider a pre-trained language model policy $\pi_\theta$ and a dataset $N$ with $(x_i, y_i)$ for $i=1$ consisting of prompts $x$ and preference-ranked completions $y_w$ and $y_l$. In this dataset, a human rater prefers $y_w$ over $y_l$, denoted as $y_w \succ y_l$. The task is to align $\pi_\theta$ with the human values implicit in these preferences. Canonically, this has been achieved through reinforcement learning from human feedback [Christiano et al., 2017, RLHF], an approach that proceeds in two phases:
- Foundation Model Proposal
- Extend/Update
- Context & Fitness
- Inner Loop Optimization Run
- CODE-LEVEL JSON FOUNDATION MODEL PROPOSAL:
{ "thought": "Based on the previous outputs,...", "name": "cross_entropy_loss", "code": "def loss_fn(logits: torch.FloatTensor, targets: torch.FloatTensor) -> torch.FloatTensor { loss = F.cross_entropy(logits, targets); return loss; }" } - SYSTEM PROMPT: You are a machine learning researcher who is testing out different loss functions.
. When you respond, output a JSON where the first key ("thought") corresponds to your thought process when designing the next function. The second key ("name") corresponds to the name of your next function. The last key ("code") corresponds to the exact python code that you would like to try. Here is an example: { } : Propose the next one to evaluate. ⇒Add evals & perf.
- Inner Loop Evaluation of Proposed Objective
- LLM-Driven Discovery
- Discovered Policy Optimization (DiscoPOP)
- ⇒Extract validation metric to optimize in outer loop
- Offline RLHF Training
First, a reward modeling stage that learns a parameterized reward model $r_\phi$. By assuming a Bradley-Terry model [Bradley and Terry, 1952] of preferences, the probability of the data can be expressed as $P(y_w \succ y_l) = \frac{\exp(r_\phi(y_w, x))}{\exp(r_\phi(y_w, x)) + \exp(r_\phi(y_l, x))}$, and subsequently simply optimized over $\phi$ through the maximum likelihood principle. The second stage of policy optimization employs a reinforcement learning algorithm to train the language model against the learned reward. Usually, a KL penalty is introduced between the model and the pre-RL reference policy $\pi_{\text{ref}}$ [Jaques et al., 2019; Stiennon et al., 2020] to prevent over-optimization and straying too far from the original policy, resulting in the final objective:
\[\max_{\pi_\theta} \mathbb{E}_{y \sim \pi_\theta, x \sim P} [r_\phi(y, x)] - \beta \text{KL}(\pi_\theta, \pi_{\text{ref}})\]Despite success in frontier models [Anthropic, 2023; Gemini-Team, 2023], deep RL has many implementation [Engstrom et al., 2019] and training challenges [Sutton, 1984; Razin et al., 2023] that hinder its adoption. In order to simplify the whole process, direct preference optimization [Rafailov et al., 2023; DPO] aims to forego both the reward modeling and online RL procedure. Rewriting (1) with a decomposition of the KL term into:
\[\max_{\pi_\theta} \mathbb{E}_{y \sim \pi_\theta, x \sim P} \left[ r_\phi(y, x) + \beta \log \frac{\pi_{\text{ref}}(y | x)}{\pi_\theta(y | x)} + \beta H(\pi_\theta) \right]\]| expresses the problem as an entropy-regularised RL bandit task [Ziebart et al., 2008], for which a known analytical solution exists: $\pi^*(y | x) = \frac{Z(x)^{-1} \exp(\beta^{-1}r_\phi(y, x))}{\pi_{\text{ref}}(y | x)}$. By rearranging the reward, we can express the task as a binary classification problem based on the reward difference: |
| Here, we define the log ratio difference as $\rho = \log \frac{\pi_\theta(y_w | x)}{\pi_{\text{ref}}(yl | x)}$. In DPO, the function $f = \log \sigma$ is derived as the negative log of the sigmoid function given the BT model assumptions. However, Tang et al. [2024] highlighted that more generally we can obtain a recipe for offline RL by letting $f$ be any scalar loss function. For example, preference optimization algorithms by letting $f(x) = (x - 1)^2$, the squared loss function [Rosasco et al., 2004] yields IPO [Azar et al., 2023], while employing the max-margin inspired hinge loss [Boser et al., 1992; Cortes and Vapnik, 1995] $f(x) = \max(0, 1 - x)$ produces SLiC [Zhao et al., 2023]. |
Meta-Optimization for Algorithm Discovery
| The goal of meta-optimization (optimizing the optimization process) is to uncover novel learning algorithms using a data-driven process. Suppose that an algorithm uses an objective function $f_\gamma$ to train a model for $K$ iterations, where $\gamma$ denotes a set of meta-parameters. Meta-optimization searches for an objective that maximizes the expected train $\mathbb{E}[\eta(\pi^K) | f_\gamma]$ where $\eta$ is a downstream performance metric. |
3 LLM-Driven Objective Discovery
Choosing an appropriate objective function is crucial for instilling capabilities into networks. Here, we detail our discovery process facilitated by LLM code-level objective function proposals:
Initial Context Construction. In the initial system prompt, we ‘burn-in’ the LLM using several established objective functions given in code and their corresponding performance. Furthermore, we provide problem details and an example of the output response format as a JSON dictionary.
LLM Querying, Parsing & Output Validation. We query the LLM, parse the response JSON, and run a set of unit tests (e.g. for valid output shapes) before starting a training run. If the parsing or unit tests fail, we resample a new solution after providing the error message as feedback to the LLM.
Performance Evaluation. The proposed objective function is then evaluated based on its ability to optimize a model for a predefined downstream validation task. We refer to the resulting performance metric as η.
Iterative Refinement. By using the performance provided as feedback, the LLM iteratively refines its proposals. In each iteration, the model synthesizes a new candidate loss function, exploring both variations of previously successful formulas and entirely new formulations that might improve upon the existing benchmarks. This iterative process is repeated for a specified number of generations or until convergence when a set of optimal loss functions is observed.
We summarise this general objective discovery process in Figure 1 and is shown in Algorithm 1.
Algorithm 1 LLM-Driven Objective Discovery
\begin{align}
\text{Algorithm 1: LLM-Driven Objective Discovery}
1:& \text{ Initialize LLM with established loss functions and their performance in context.}
2:& \text{ repeat for each generation } i
3:& \quad \text{LLM proposes a new candidate objective function } f_i
4:& \quad \text{Run unit tests to check validity of the candidate and resample if needed.}
5:& \quad \text{Evaluate the objective function using the performance metric } \eta
6:& \quad \text{Update the LLM context with the performance data}
7:& \quad \text{LLM refines generation strategy based on the feedback}
8:& \text{until convergence criteria are met or maximum generations are reached}
\end{align}
LLM proposes a new candidate objective function fi Run unit tests to check validity of the candidate and resample if needed. Evaluate the objective function using the performance metric η Update the LLM context with the performance data LLM refines generation strategy based on the feedback
Small case study: Discovering supervised classification loss functions. Consider the case of supervised classification on the CIFAR-10 dataset as a simple starting example. We train a simple ResNet-18 for 5 epochs using the objectives proposed by GPT-4 [OpenAI, 2023]. After each training run we provide the LLM with the corresponding validation accuracy and query it for the next PyTorch-based [Paszke et al., 2017] candidate objective function.
Figure 2: LLM-driven objective discovery for CIFAR-10 classification. Left. Performance across LLM-discovery trials. The proposals alternate between exploring new objective concepts, tuning the components, and combining previous insights. Right. The best three discovered objectives transfer to different network architectures and longer training runs (100 epochs).
Figure 2 depicts the performance of the proposed objective functions across the discovery process. The different discovered objectives all outperform the standard cross-entropy loss. Interestingly, we observe that the LLM-driven discovery alternates between several different exploration, fine-tuning, and knowledge composition steps: Initially, the LLM proposes a label-smoothed cross-entropy objective. After tuning the smoothing temperature, it explores a squared error loss variant, which improved the observed validation performance. Next, the two conceptually different objectives are combined, leading to another significant performance improvement. Hence, the LLM discovery process does not perform a random search over objectives previously outlined in the literature but instead composes various concepts in a complementary fashion. Furthermore, the discovered objectives also generalize to different architectures and longer training runs. In Appendix D.3 we show that this process of discovery is robust to the choice of sampling temperature and prompt/context construction.
4 Discovering Offline Preference Optimization Objectives
In this section, we run our LLM-driven discovery to automatically generate new state-of-the-art preference optimization algorithms.
4.1 Discovery Task - Multi-turn Dialogue on MT-Bench
Each objective function takes as input:
-
\(x\), $$ \log \pi_{\text{ref}}(y_w x) $$ -
\(x\), $$ \log \pi_{\text{ref}}(y_l x) $$ - \[x\]
For each valid generated objective function \(f_i\), we finetune an LLM and then collect a performance evaluation score. Specifically, we build on top of the ‘alignment-handbook’ [Tunstall et al., 2023a] repository to finetune our models. Notably, this repository, when using DPO, reproduces ‘Zephyr 7B Gemma’^2 Tunstall and Schmid [2024], Tunstall et al. [2023b], which at the time of release, achieved state-of-the-art scores on MT-Bench for 7B models. ‘Zephyr 7B Gemma’ first takes gemma-7b [Gemma-Team et al., 2024] and finetunes it on the ‘deita-10k-v0-sft’ dataset [Liu et al., 2023] to produce ‘zephyr-7b-gemma-sft’^3. It is then trained on the pairwise preference dataset of ‘Argilla DPO Mix 7K’^4. When evaluating a new objective function, we replace DPO in this last step with the generated objective function, keeping the same hyperparameters. We show example runs in Figure 3 and provide further experimental details in Appendix B.
Figure 3: Examples of LLM Objective Discovery improvement across generations. The first and second run shown left and right respectively. In this section we use our LLM-driven discovery method to discover new objective functions \(f\) for offline preference optimization, as defined in Section 2 and Equation (3). Specifically, at each generation \(i\), GPT-4 generates PyTorch [Paszke et al., 2017] code of candidate objective function \(f_i\). It uses variables \(x\), \(\log \pi_\theta(y_l)\), \(\log \pi_\theta(y_w)\), and returns a scalar. For each proposed objective \(f_i\), we check if \(f_i\) is valid with a unit test.
Once we have a trained LLM for the proposed objective function \(f_i\), we evaluate that LLM on the popular multi-turn dialogue evaluation benchmark of MT-Bench [Zheng et al., 2024]. This is a multi-turn open-ended question set, which uses GPT-4 to assess the quality of the trained model’s responses, obtaining a high correlation with the popular Chatbot Arena [Zheng et al., 2024]. We provide further evaluation details in Appendix C.
4.2 Discovery Results
Figure 4: MT-Bench Discovered Objective Evaluations
After evaluating approximately 100 objective functions, we cataloged the best-performing ones in Table 1. We tabulate the high-level objective forms here and provide the full objective loss functions and their associated code in Appendix E. Moreover, we also plot the best performing sub-task evaluations in Figure 4. Table 1: Discovery Task MT-Bench Evaluation Scores for each discovered objective function \(f\). We provide the baselines first, followed by a dashed line to separate the objective functions that were discovered. We provide details for each discovered objective function in Appendix E.
| Name | Full Name | Objective \(f\) Function | Score (/ 10) |
|---|---|---|---|
| DPO | Direct Preference Optimization Official HuggingFace ‘zephyr-7b-gemma’ DPO model | \(\log(1 + \exp(\log(1 + \exp(-\beta \rho))) - \beta \rho)\) | 7.888 |
| SLiC | Sequence Likelihood Calibration | \(\sigma(\text{Var}[\rho/\tau]) \cdot f_{\text{exp}}(\beta \rho)\) | 7.810 |
| KTO | Pairwise Kahneman-Tversky Optimization | \(q \cdot 0.9\) | 7.881 |
| DBAQL | Dynamic Blended Adaptive Quantile Loss | \(\sigma(\text{Var}[\rho/\tau])) - \cdot q) f_{\text{slic}}(\beta \rho)\) | 7.603 |
| AQL | Adaptive Quantile Loss | \(f_{\text{dpo}}(\beta \rho) + 0.5\) | 7.978 |
| PADLL | Performance Adaptive Decay Logistic Loss | \(f_{\text{dpo}}(\beta \rho/0.9) + (1 \cdot 0.5 \sigma\)rho/\tau )) $$ | 7.953 |
| AQFL | Adaptive Quantile Feedback Loss | \(f_{\text{dpo}}(\beta \rho) + \sigma\)rho/\tau ) \cdot 1[\pi_w > \pi_r] + 2 $$ | 7.941 |
| CELL | Combined Exponential + Logistic Loss | \(f_{\text{slic}}(\beta \rho) \cdot f_{\text{exp}}(\beta \rho) \cdot 1[\pi_w \leq \pi_r]\) | 7.931 |
| LRML (DiscoPOP) | Log Ratio Modulated Loss | \((1 - f_{\text{dpo}}(\beta \rho)) \cdot 1/2\) | 7.925 |
3 https://huggingface.co/HuggingFaceH4/zephyr-7b-gemma-sft-v0.1
5 Held-Out Evaluations
We next validate each of our discovered objective functions (shown in Table 1) on held-out tasks. We find that the Performance Adaptive Decay Loss (PADLL) and the Log Ratio Modulated Loss (LRML) consistently perform well. Because of its unconventional properties and performance, we refer to LRML as our discovered preference optimization, or DiscoPOP, algorithm.
We consider three different standard [Rafailov et al., 2023] open-ended text generation tasks each designed to evaluate different properties of the fine-tuned LLM policy \(\pi_\theta\) where each LLM policy is trained with one of our discovered objective functions \(f\) on a preference dataset
\[\{ (x_i, y_i^w, y_i^l) \}_{i=1}^N\]5.1 Single-turn Dialogue - Alpaca Eval 2.0
We evaluate the trained models on Alpaca Eval 2.0, [Li et al., 2023, Dubois et al., 2023, 2024]. This is a single-turn dialogue LLM-based automatic evaluation using GPT-4 to assess the win rate of the trained LLM policy’s completion compared to the of the underlying SFT base model. Alpaca Eval 2.05, has been validated against 20K human annotations, and aims to reduce the length bias of Alpaca Eval 1.0; where using length controlled (LC) Alpaca Eval shows a correlation with Chatbot Area of 0.98, making it a popular benchmark with the highest correlation to Chatbot Arena [Dubois et al., 2024]. We also detail task training details in Appendix B.1. Table 2: Alpaca Eval 2.0 - Held Out Single Turn Dialogue Task. Win rate of the discovered objective functions f evaluated on the Alpaca Eval 2.0 task against either GPT-4 or the SFT base model. Some of the discovered objective functions outperform the baselines, with the best bolded. We detail evaluation and error bars in Appendix C. We have highlighted the best scores with overlapping the standard errors.
We provide the Alpaca Eval 2.0 results in Table 2. As reference policies, we used GPT-4 for absolute comparison and the SFT-trained model for relative comparison. We observe that the discovered LRML (DiscoPOP), PADLL, and AQFL functions outperform the baselines and other discovered losses on the normal and length-controlled win rates. The differences in scores among these top performing losses are not significant, except for the LC win rate against the SFT reference model, where DiscoPOP performs best.
5.2 Summarization (TL;DR)
We train an LLM policy to, given a forum post on Reddit x, generate a summarization y of the main points. We finetune ‘zephyr-7b-gemma-sft‘ using 10% of the Reddit TL;DR summarization preference dataset [Völske et al., 2017] on each of the baseline and discovered objective functions. As a reference model, we again use ‘zephyr-7b-gemma-sft’. Further details on the training pipeline are outlined in Appendix B.2. To evaluate the quality of the summaries, we make use of the Alpaca Eval 2.0 library with a custom evaluation dataset existing of 694 test samples from the TL;DR dataset and a custom GPT-4 annotator template as described in Rafailov et al. [2023]. For additional details regarding the summarization evaluation see Appendix C.3.
In Table 3 the PADLL loss and DPO loss perform best, with little difference from each other, on the summarization task in three out of four metrics. Additionally, the LRML - DiscoPOP function achieves scores slightly below the top performers, especially in the length-controlled win rates. In contrast to the single-turn dialogue task, the AQFL loss does not achieve high scores in the held-out evaluation.
Table 3: TL;DR - Held Out Summarization Task Win rate of various preference optimization functions in the summarization task evaluated with the Alpaca Eval 2.0 calculations, against a subset of the test set (694 samples). The baseline outputs are the human generated preferences, and the model after SFT (see Appendix C for details). Note that the standard error in the LC win-rate has been rounded down because of values < 0.001. We have highlighted the scores with means overlapping the standard error of the best score.
In this task, we train an LLM policy to generate movie review completions y with positive sentiment, where x is a prompt at the start of a movie review from the IMDb dataset [Maas et al., 2011]. We start with a GPT-2 [Radford et al., 2019] model, which had supervised fine-tuning on the IMDb dataset, and we perform preference optimization using the baseline and discovered objective loss functions. Details of the training implementations can be found in Appendix B.3. Inspired by Rafailov et al. [2023]’s experiments, we calculate the model rewards through a pre-trained sentiment classifier, which we use as a proxy for ground truth, as well as the KL-Divergence of the trained model and the reference model. Appendix C.4 provides further details into the evaluation for this task.
We provide results of models with converging β values in Figure 5 for LRML compared against DPO and SLiC, displaying the model rewards against the KL-Divergence to the reference model. In Figure 5a, the LRML-trained text generator outperforms the DPO model in terms of rewards and KL-divergence with low β values (0.025, 0.05, 0.1). At higher β values (0.5 and 1.0) both methods show trends of increased KL-Divergence and lower rewards, but generally LRML maintains a higher reward than DPO. In Figure 5b, we note that LRML slightly outperforms DPO, SLiC, AQFL, and PADLL at β in terms of reward. For larger β values (0.5 and 1.0), LRML shows similar trends of increased KL-Divergence and rewards like the other objective functions. A more detailed comparison between the individual discovered losses and the baselines can be found in Appendix Figure 8.
6 Analysis of DiscoPOP
We list all our discovered objectives in Table 1, as well as the code and mathematical representations in Appendix E. In this section, we now analyze the Log Ratio Modulated Loss, which we define as the DiscoPOP loss function, as it performs consistently high across the held-out evaluation tasks, and we provide some intuitive understanding of how it outperforms the existing state-of-the-art objectives.
6.1 Log Ratio Modulated Loss (DiscoPOP)
The Log Ratio Modulated Loss is a dynamically weighted sum of the logistic loss (as used in DPO) and the exponential loss. The weight of each is determined through a sigmoid calculation of the difference of log-ratios (\(\rho\)). Mathematically, the LRML function can be described with a temperature parameter \(\tau = 0.05\) as follows:
\(f_{\text{lrml}}(\beta \rho) = (1 - \sigma\)rho/\tau)) f_{\text{dpo}}(\beta \rho) + \sigma\(rho/\tau) \log(1 + \exp(\beta \rho))\)
If the difference of log ratios is zero (\(\rho = 0\)), which is at the start of the training when the model policy \(\pi_\theta\) is equal to the reference policy \(\pi_{\text{ref}}\), then the loss is equally balanced between the logistic and exponential loss. If \(\rho \rightarrow \infty\), the model policy diverges from the reference policy and chosen outputs are preferred, then the exponential term dominates. This emphasizes larger differences more strongly. On the other hand, if \(\rho \rightarrow -\infty\), the model policy diverges from the reference policy and rejected outputs are preferred. In this case, the logistic loss can handle moderate differences well.
The baseline objective losses and the LRML, the PADLL, and the AQFL functions are displayed in Figure 6, including their gradients. Surprisingly, we see that the DiscoPOP function has a non-convex segment and negative gradients at the starting point \(\rho = 0\). This is potentially helpful for introducing a curriculum or for stochasticity.
(a) DPO vs LRML
(b) Discovered vs Baseline Losses
Figure 5: Frontiers of expected reward vs KL divergence for converging models for the LRML against DPO and SLiC objective function. The rewards and KL-divergence values are averaged over 10 generations with different seeds. The sweep is done over \(\beta \in \{0.025, 0.05, 0.1, 0.25, 0.5, 1.0\}\). The optimal point is the top left corner, where the perfect reward is achieved with minimal divergence from the reference model.
(a) Discovered Objective Functions
(b) Gradients of the Discovered Objective Functions
Figure 6: Figure 6a: Baseline objective functions DPO and SLiC, and the discovered ones, LRML, AQFL, and PADLL. Figure 6b: gradients of the objectives as a function of \(\rho\) and with fixed \(\beta = 0.05\).
6.2 Limitations of DiscoPOP
While performing very well on single-turn text generation and text summarization, we observed during the IMDb experiment that LRML struggles to converge when \(\beta\) is too low (\(\beta \leq 0.01\)) or too high (\(\beta \geq 2.5\)), likely because \(\beta\) was never seen or used during the discovery process.
In Figure 9 and Figure 10 of the Appendix, we plot the LRML objective function for \(\beta \in \{0.01, 0.025, 0.05, 0.1, 0.25, 0.5, 1, 2.5, 5\}\) against DPO. Notably, when \(\beta\) is high, the DiscoPOP objective function takes the form of the DPO log sigmoid loss. During training on \(\beta = 0.01\), we observed that DiscoPOP gets stuck in generating negative reviews. We hypothesize that it is because the loss is stuck in the local-minima to the left with negative difference of log-ratios. While training with \(\beta = 2.5, 5.0\) we observed that the model collapsed after a sharp spike in the loss and subsequently having loss value 0 and NaN outputs. This is potentially due to large gradient in the non-convex part, which could potentially be amended with gradient clipping.
7 Related Work
Evolution and Search with Large Language Models. LLMs provide a fast and automated way to create multiple candidate solutions for a problem stated in natural language [Song et al., 2024]. This makes them powerful tools for driving population-based search procedures such as evolutionary meta-discovery. Various recent works have applied this approach to coding problems [Romera-Paredes et al., 2024], neural architecture search [Chen et al., 2024a], virtual robotic design settings [Lehman et al., 2023], and reward functions [Ma et al., 2023, Yu et al., 2023]. Finally, recently LLMs have shown to be capable of acting as recombination operators for black-box optimization with Evolution Strategies [Lange et al., 2024] and for Quality-Diversity approaches [Lim et al., 2024].
Automated Discovery for Machine Learning. There are many other approaches to automating the discovery of generalizable machine learning algorithms. Some prior works explore the space of ML functions using genetic algorithms and a hand-crafted domain-specific language for reinforcement learning algorithms [Co-Reyes et al., 2021], curiosity algorithms [Alet et al., 2020], and optimizers [Chen et al., 2024b]. Other works instead parameterize a transferrable objective function using neural networks and optimize them with evolution strategies. For example, Lu et al. [2022], Jackson et al. [2024], Houthooft et al. [2018], Alfano et al. [2024] evolve policy optimization objectives, Metz et al. [2022] evolves neural network optimizers, and Lange et al. [2023b,a] evolve blackbox optimizers.
Preference Optimization Algorithms. While the reduction to supervised learning makes DPO and alternatives easier to use, other approaches have sought to simplify the RL step, including using variants of REINFORCE [Ahmadian et al., 2024, Gemma-Team et al., 2024] as well as more fine-grained feedback [Wu et al., 2024] through preferences over individual steps in the reasoning process [Uesato et al., 2022, Lightman et al., 2023] or reward redistribution [Chan et al., 2024]. Others use iterative offline training interleaved with sampling from the policy model and obtaining a preference ranking from themselves [Xu et al., 2023], another judge LLM [Guo et al., 2024], or an oracle [Swamy et al., 2024].
8 Conclusion
Summary. In this paper, we proposed and used LLM-driven objective discovery to generate novel offline preference optimization algorithms. Specifically, we were able to discover high-performing preference optimization losses that achieve strog performance across held-out evaluation tasks, with the highest performing providing new insights into what an optimal objective may need to possess, such as being a blend of logistic and exponential losses, and possibly be non-convex.
Limitations & Future work. There are multiple limitations of our current approach. First, we have only scratched the surface of how to generate LLM objective proposals most effectively. Initial exploratory experiments using techniques such as temperature sampling or worst-to-best performance sorting in the context did not yield significant improvements. But one could imagine leveraging more information about the training runs and automatically tuning instruction prompt templates. E.g. by providing entire learning curve plots to a Visual Language Model (see Figure 12) or by meta-optimizing [Lu et al., 2023] the LLM prompt. Second, the highest-performing loss re-purposed β in the traditional sense, making it affect the functional behavior as well as the KL penalty of the model with respect to the base model. This motivates future work to study different forms, with perhaps multiple floating point parameters in the form, that each could be tuned separately. Although we provided an initial analysis sweep over this one single parameter and observed some instances of the functional behavior leading to instability of training the model, a further multi-parameter analysis, reformulating the objective, would be beneficial for future work. Finally, our work uses closed-source models (GPT-4) to generate code, which limits reproducibility and is costly to run. Future work could use the produced models themselves to generate code, resulting in code-level self-improvement.
Broader Impact and Ethical Considerations. This paper presents an LLM-driven discovery in-context learning pipeline that is used to generate better-performing novel offline preference optimization algorithms. However, misuse of the pipeline as a tool or training an LLM to produce undesirable, unethical, or harmful outputs could be possible by a user. Furthermore, due to the use of LLMs and training of LLMs, the outputs are susceptible to hallucinations, motivating all outputs of the LLMs to always have a content filter applied to the outputs. Finally, this work takes a small step towards code-level self-improvement in language models, which could potentially result in unintended behaviors.