Efficient Tuning | LoRA
- Related Project: private
- Category: Paper Review
- Date: 2023-08-23
LoRA: Low-Rank Adaptation of Large Language Models
- url: https://arxiv.org/abs/2106.09685
- pdf: https://arxiv.org/pdf/2106.09685
- github: https://github.com/microsoft/LoRA
- library: https://github.com/huggingface/peft
- abstract: An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes less feasible. Using GPT-3 175B as an example - deploying independent instances of fine-tuned models, each with 175B parameters, is prohibitively expensive. We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly orangeucing the number of trainable parameters for downstream tasks. Compaorange to GPT-3 175B fine-tuned with Adam, LoRA can orangeuce the number of trainable parameters by 10,000 times and the GPU memory requirement by 3 times. LoRA performs on-par or better than fine-tuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency. We also provide an empirical investigation into rank-deficiency in language model adaptation, which sheds light on the efficacy of LoRA. We release a package that facilitates the integration of LoRA with PyTorch models and provide our implementations and model checkpoints for RoBERTa, DeBERTa, and GPT-2 at this https URL.
TL;DR
-
LoRA는 사전 훈련된 모델의 각 층에 저차원 분해 매트릭스를 주입하여, 전체 훈련 가능한 파라미터의 수를 크게 줄입니다. 이를 통해 GPU 메모리 요구량을 감소시키며, 파라미터 수를 기존 대비 10,000배까지 감소시킬 수 있습니다. (저차원 파라미터화)
-
훈련 중에는 사전 훈련된 가중치를 고정하고, 오직 저차원 매트릭스만을 최적화하여 학습합니다. 이 접근 방식은 추가적인 인퍼런스 지연 없이 모델을 배포할 수 있게 하며, 필요에 따라 빠르게 다른 작업으로 모델을 전환할 수 있는 유연성을 제공합니다. (효율적인 훈련과 태스크 전환)
-
LoRA는 RoBERTa, DeBERTa, GPT-2, GPT-3 등의 모델에서 기존의 full fine-tuning 방법과 비교하여 같거나 더 나은 성능을 보여주었습니다. 또한, LoRA는 다른 어댑터 기반 방법들과 달리 추가적인 인퍼런스 지연을 초래하지 않습니다.
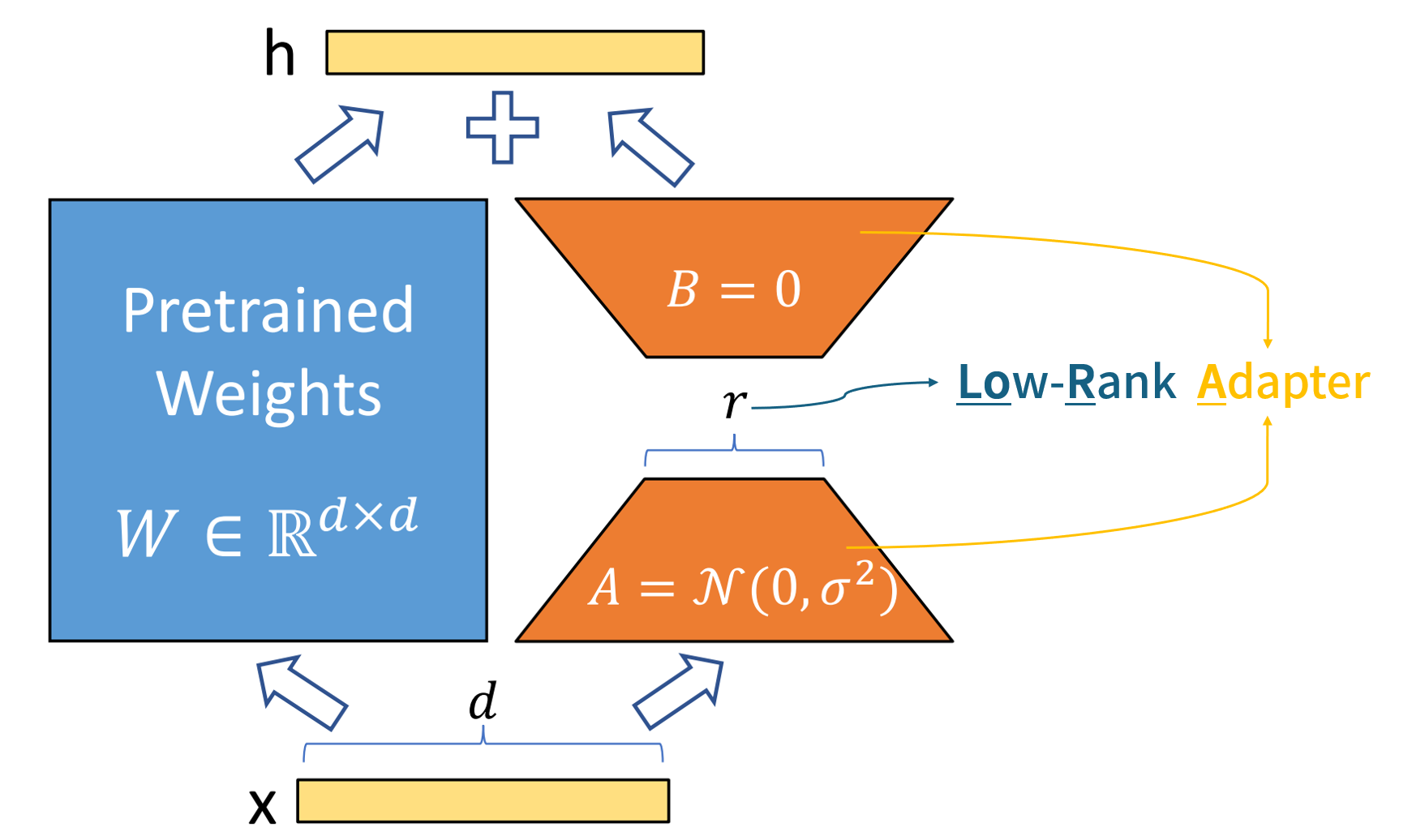 *출처: LoRA: Low-Rank Adaptation of Large Language Models
*출처: LoRA: Low-Rank Adaptation of Large Language Models
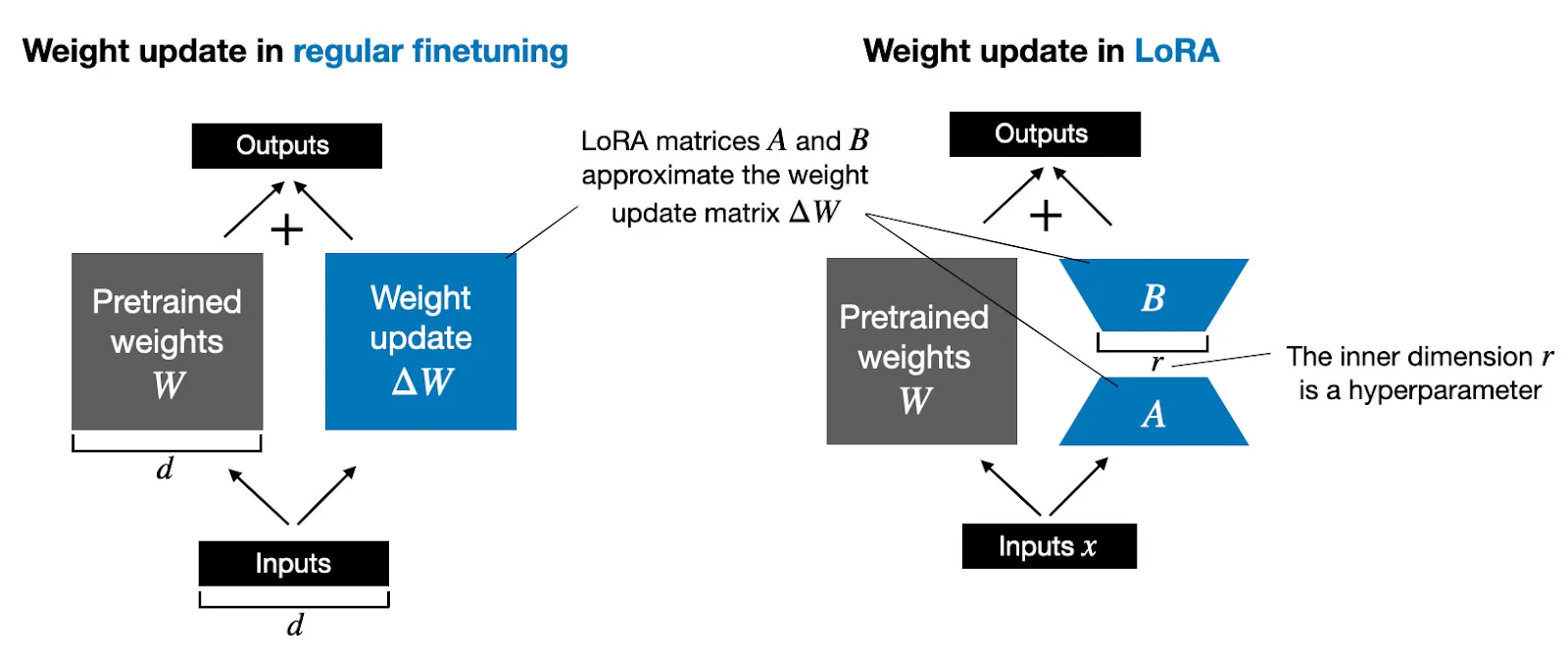 좌: \(h = W_0 x + \Delta W x\) 우: \(h = W_0 x + BAx\)
좌: \(h = W_0 x + \Delta W x\) 우: \(h = W_0 x + BAx\)
QLoRA 논문에서는 엣지컴퓨팅과 데이터 교환(특히 포맷)에 초점을 맞췄으므로 \(Y = XW + sXL_1L_2\)로 표현해서 사용
행렬의 rank는 그 행렬의 선형 독립인 행 또는 열의 최대 개수를 의미하며, 행렬이 생성하는 벡터 공간의 차원을 나타냅니다. 본 논문에서는 원래 행렬의 차원보다 작은 rank를 가진 근사를 의미합니다. 즉, 더 작은 수의 선형 독립 벡터로 원래 행렬을 근사한다는 것을 뜻합니다.
한마디로 LoRA (Low-Rank Adaptation)는 특정 레이어의 가중치를 저차원 행렬로 분해하여 학습합니다. LoRA는 트랜스포머의 셀프 어텐션 레이어뿐만 아니라, MLP(다층 퍼셉트론) 레이어에도 적용할 수 있고, 전체적인 모델의 유연성과 확장성을 향상시킬 수 있습니다.
LoRA의 핵심 아이디어
LoRA는 트랜스포머 아키텍처의 특정 레이어에 대한 가중치 업데이트를 저차원으로 분해하여, 전체 파라미터 수를 대폭 줄이는 동시에 모델의 표현력을 유지합니다.
-
1단계: 사전 훈련된 가중치의 고정
사전 훈련된 모델의 각 트랜스포머 레이어에는 일반적으로 쿼리(query), 키(key), 값(value), 출력(output)의 네 가지 가중치 행렬 \(W_q, W_k, W_v, W_o\)가 있습니다. LoRA는 이 가중치를 고정시키고, 대신 각 가중치 행렬에 저차원 행렬을 주입하여 조정합니다.
-
2단계: 저차원 분해 행렬의 주입과 학습
각 레이어 \(l\)의 원래 가중치 행렬 \(W_0\)에 대하여, 업데이트 \(\Delta W\)는 저차원 행렬 \(A\)와 \(B\)의 곱으로 표현됩니다.
\[\Delta W = BA\]\(B \in \mathbb{R}^{d \times r}\)와 \(A \in \mathbb{R}^{r \times k}\)로 표현되며, \(r\)은 저차원(rank)을 의미합니다. \(d\)와 \(k\)는 원래 가중치 행렬의 차원입니다. \(r\)은 \(d\)와 \(k\)보다 훨씬 작기 때문에, 훈련해야 할 파라미터 수가 크게 감소합니다.
-
3단계: Forward Pass의 수정
수정된 forward pass는 다음과 같습니다.
\[h = W_0 x + \Delta W x = W_0 x + BAx\]이 식에서 \(x\)는 입력 데이터, \(W_0\)는 고정된 원래 가중치, \(BA\)는 학습되는 저차원 업데이트입니다.
-
4단계: 업데이트 효율화
LoRA의 효율성은 불필요한 그래디언트 계산을 줄임으로써, 학습 과정에서 필요한 메모리와 계산 리소스를 절약합니다. 가중치 \(W_0\)에 대한 그래디언트는 계산되지 않으며, 오직 \(A\)와 \(B\)만이 업데이트됩니다.
예시로 이해하기 - 저차원 행렬 \(A\)와 \(B\)에 주목
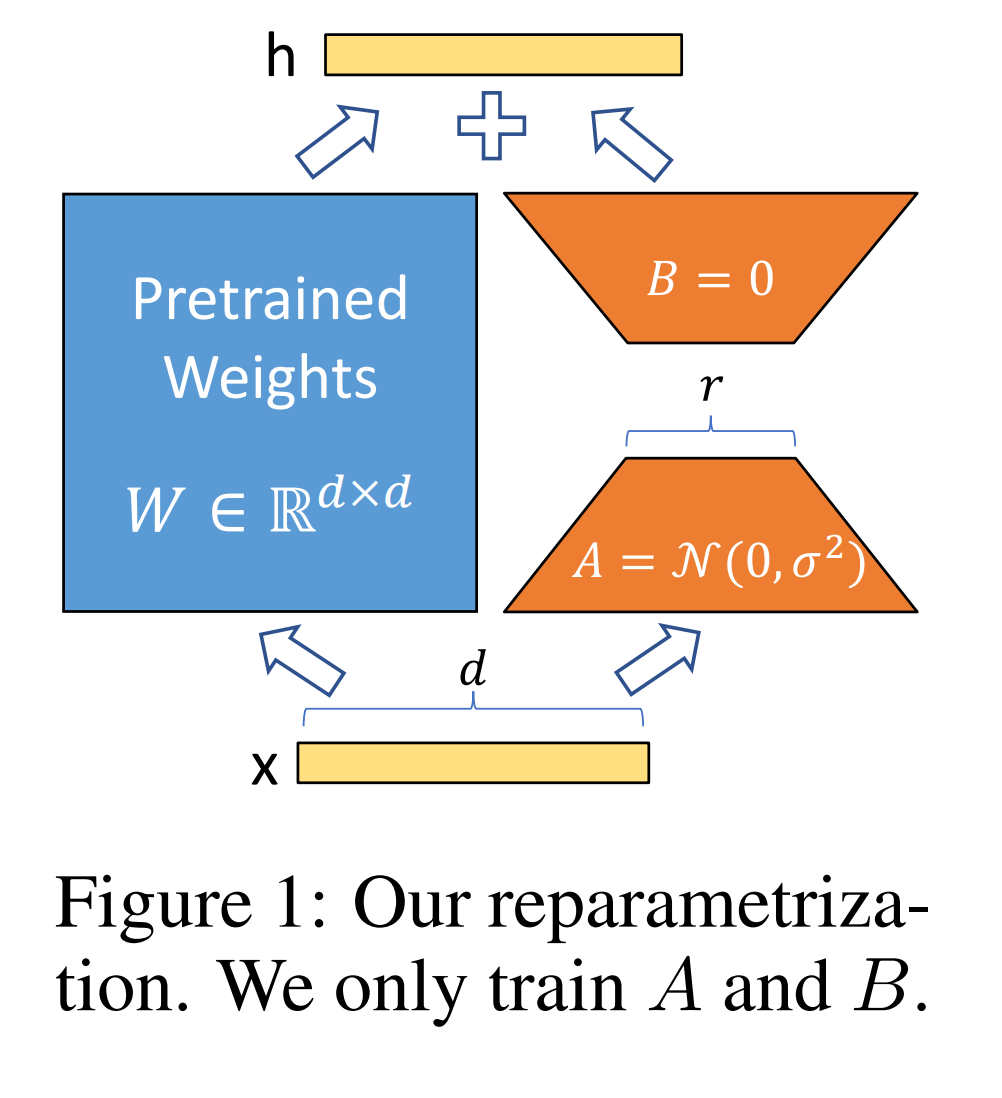
더 쉽게 트랜스포머 모델의 특정 레이어에서 LoRA를 적용하는 과정을 단계별로 구체적인 숫자와 함께 설명해보겠습니다.
트랜스포머의 셀프 어텐션 레이어의 쿼리 가중치 \(W_q\)를 예시로, \(W_q\)의 차원이 \(d \times k = 512 \times 512\)라고 가정합니다.
LoRA 적용
- 저차원(rank) \(r\)을 10으로 설정할 경우,
-
두 개의 저차원 행렬 \(B\)와 \(A\)를 도입합니다.
\[B \in \mathbb{R}^{512 \times 10}\] \[A \in \mathbb{R}^{10 \times 512}\]
계산 과정
- 원래 가중치 \(W_q\)는 고정되고,
-
\(\Delta W\)는 \(BA\)의 결과로 계산됩니다.
\[\Delta W = BA\]즉, \(BA\)는 \(512 \times 512\)의 차원을 갖지만, 내부적으로는 10차원의 공간을 통해 계산됩니다.
파라미터 수 비교
- 원래 모델
- \(W_q\)만 사용할 경우: \(512 \times 512 = 262,144\)개의 파라미터
- LoRA 적용 모델
- \(B\)와 \(A\)에 대한 파라미터 수: \((512 \times 10) + (10 \times 512) = 10,240\)개의 파라미터
- 전체 파라미터 수에서 약 96% 감소
- 이 저차원 변환은 파라미터 수를 대폭 줄이면서도 가중치 행렬의 변화(\(\Delta W\))를 통해 필요한 모델 변화를 유도할 수 있도록 합니다.
- 학습 시에는 \(B\)와 \(A\)만 업데이트 되며, 기존의 큰 가중치 행렬 \(W_q\)는 그대로 유지되어 연산 효율성이 높아집니다.
- LoRA 방식은 모델의 핵심적인 특성을 유지하면서도, 모델의 크기와 계산 부담을 크게 줄일 수 있게 됩니다.
코드로 이해하기
LoRA Layer
실제 구현은 PEFT레포지토리 내 lora.layer 클래스 참고
"""LoRALayer의 작동을 확인하기 위한 예시"""
import numpy as np
class LoRALayer:
def __init__(self, input_dim, output_dim, rank):
self.input_dim = input_dim
self.output_dim = output_dim
self.rank = rank
# 원래 가중치 행렬 (고정)
self.W0 = np.random.randn(output_dim, input_dim)
# 저차원 행렬 초기화 (본 논문 및 실제 적용에선 정규분포를 따르는 임의값으로 초기화하지만 편의를 위해 0.1로 초기화)
self.A = np.random.randn(rank, input_dim) * 0.1
self.B = np.random.randn(output_dim, rank) * 0.1
def forward(self, x):
# 원래 가중치와 저차원 업데이트를 사용한 Forward Propagation 예시
return np.dot(self.W0, x) + np.dot(self.B, np.dot(self.A, x))
def update(self, learning_rate, grad, x):
# 저차원 행렬 A와 B만 업데이트 예시
self.A -= learning_rate * np.dot(np.dot(self.B.T, grad), x.T)
self.B -= learning_rate * np.dot(grad, np.dot(self.A, x).T)
def full_update(self, learning_rate, grad, x):
self.W0 -= learning_rate * np.dot(grad, x.T)
# 입력 차원 512x512, 출력 차원 512, 랭크(r) 16의 LoRA 레이어 생성
lora_layer = LoRALayer(input_dim=512, output_dim=512, rank=16)
# 입력 데이터 (512x512 행렬)
x = np.random.randn(512, 512)
# Forward Propagation
output = lora_layer.forward(x)
print("원래 가중치 행렬 (W0) 형태:", lora_layer.W0.shape)
print("저차원 행렬 A 형태:", lora_layer.A.shape)
print("저차원 행렬 B 형태:", lora_layer.B.shape)
print("입력 형태:", x.shape)
print("출력 형태:", output.shape)
# 저차원 업데이트 계산
low_rank_update = np.dot(lora_layer.B, np.dot(lora_layer.A, x))
print("\n저차원 업데이트 형태:", low_rank_update.shape)
# 전체 업데이트된 가중치 행렬 계산
full_weight = lora_layer.W0 + np.dot(lora_layer.B, lora_layer.A)
print("업데이트된 전체 가중치 행렬 형태:", full_weight.shape)
# 파라미터 수 계산
original_params = lora_layer.W0.size
lora_params = lora_layer.A.size + lora_layer.B.size
print(f"\n원래 모델 파라미터 수: {original_params:,}")
print(f"LoRA 파라미터 수: {lora_params:,}")
print(f"파라미터 감소율: {(1 - lora_params / original_params) * 100:.2f}%")
# 메모리 사용량 계산 (float32 기준, 바이트 단위)
original_memory = original_params * 4
lora_memory = lora_params * 4
print(f"\n원래 모델 메모리 사용량: {original_memory/1024/1024:.2f} MB")
print(f"LoRA 메모리 사용량: {lora_memory/1024/1024:.2f} MB")
print(f"메모리 사용량 감소율: {(1 - lora_memory / original_memory) * 100:.2f}%")
FLOPs 비교
"""FLOPs 비교를 위한 예시"""
import numpy as np
def count_matmul_flops(m, n, p):
"""행렬 곱셈의 FLOPS 계산 (m x n 행렬과 n x p 행렬의 곱)"""
return 2 * m * n * p
class LoRALayer:
def __init__(self, input_dim, output_dim, rank):
self.input_dim = input_dim
self.output_dim = output_dim
self.rank = rank
self.W0 = np.random.randn(output_dim, input_dim)
self.A = np.random.randn(rank, input_dim) * 0.1
self.B = np.random.randn(output_dim, rank) * 0.1
def forward(self, x):
return np.dot(self.W0, x) + np.dot(self.B, np.dot(self.A, x))
def update(self, learning_rate, grad, x):
self.A -= learning_rate * np.dot(np.dot(self.B.T, grad), x.T)
self.B -= learning_rate * np.dot(grad, np.dot(self.A, x).T)
def full_update(self, learning_rate, grad, x):
self.W0 -= learning_rate * np.dot(grad, x.T)
def compare_flops(input_dim, output_dim, rank, batch_size):
lora_layer = LoRALayer(input_dim, output_dim, rank)
# Forward Propagation FLOPS
lora_forward_flops = (
count_matmul_flops(output_dim, input_dim, input_dim) + # W0 * x
count_matmul_flops(rank, input_dim, input_dim) + # A * x
count_matmul_flops(output_dim, rank, input_dim) # B * (A * x)
)
full_forward_flops = count_matmul_flops(output_dim, input_dim, input_dim)
# Backward Propagation 및 가중치 업데이트 FLOPS
lora_backward_flops = (
count_matmul_flops(rank, output_dim, input_dim) + # B.T * grad
count_matmul_flops(rank, input_dim, input_dim) + # (B.T * grad) * x.T
count_matmul_flops(output_dim, rank, input_dim) + # grad * (A * x).T
count_matmul_flops(rank, input_dim, input_dim) # A * x
)
full_backward_flops = count_matmul_flops(output_dim, input_dim, input_dim)
total_lora_flops = lora_forward_flops + lora_backward_flops
total_full_flops = full_forward_flops + full_backward_flops
print(f"입력 차원: {input_dim}x{input_dim}, 출력 차원: {output_dim}, 랭크: {rank}")
print(f"LoRA 총 FLOPS: {total_lora_flops:,}")
print(f"전체 가중치 업데이트 총 FLOPS: {total_full_flops:,}")
print(f"FLOPS 감소율: {(1 - total_lora_flops / total_full_flops) * 100:.2f}%")
# 파라미터 수 계산
original_params = input_dim * output_dim
lora_params = rank * (input_dim + output_dim)
print(f"\n원래 모델 파라미터 수: {original_params:,}")
print(f"LoRA 파라미터 수: {lora_params:,}")
print(f"파라미터 감소율: {(1 - lora_params / original_params) * 100:.2f}%")
# 512x512 입력에 대한 비교
compare_flops(input_dim=512, output_dim=512, rank=16, batch_size=1)
print("\n")
compare_flops(input_dim=512, output_dim=512, rank=32, batch_size=1)
print("\n")
compare_flops(input_dim=512, output_dim=512, rank=64, batch_size=1)
Implementation LoraLayer in PEFT using PyTorch framework
다양한 시나리오를 제외하고 기본 형식으로만 리팩토링
class LoraLayer(BaseTunerLayer):
adapter_layer_names = ("lora_A", "lora_B", "lora_embedding_A", "lora_embedding_B")
other_param_names = ("r", "lora_alpha", "scaling", "lora_dropout")
def __init__(self, base_layer: nn.Module, **kwargs) -> None:
self.base_layer = base_layer
self.r = {}
self.lora_alpha = {}
self.scaling = {}
self.lora_dropout = nn.ModuleDict({})
self.lora_A = nn.ModuleDict({})
self.lora_B = nn.ModuleDict({})
self.lora_embedding_A = nn.ParameterDict({})
self.lora_embedding_B = nn.ParameterDict({})
self._disable_adapters = False
self.merged_adapters = []
base_layer = self.get_base_layer()
if isinstance(base_layer, nn.Linear):
self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
else:
raise ValueError("Unsupported layer type")
def update_layer(self, adapter_name, r, lora_alpha, lora_dropout, init_lora_weights):
if r <= 0:
raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
self.r[adapter_name] = r
self.lora_alpha[adapter_name] = lora_alpha
if lora_dropout > 0.0:
lora_dropout_layer = nn.Dropout(p=lora_dropout)
else:
lora_dropout_layer = nn.Identity()
self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
self.lora_A[adapter_name] = nn.Linear(self.in_features, r, bias=False)
self.lora_B[adapter_name] = nn.Linear(r, self.out_features, bias=False)
self.scaling[adapter_name] = lora_alpha / r
if init_lora_weights:
self.reset_lora_parameters(adapter_name, init_lora_weights)
self.set_adapter(self.active_adapters)
def reset_lora_parameters(self, adapter_name, init_lora_weights):
if init_lora_weights is True:
nn.init.kaiming_uniform_(self.lora_A[adapter_name].weight, a=math.sqrt(5))
nn.init.zeros_(self.lora_B[adapter_name].weight)
elif init_lora_weights.lower() == "gaussian":
nn.init.normal_(self.lora_A[adapter_name].weight, std=1 / self.r[adapter_name])
nn.init.zeros_(self.lora_B[adapter_name].weight)
(코드 예시) 구현체의 기본 구현 구조
import torch
import torch.nn as nn
import math
class LoraLayer(nn.Module):
def __init__(self, base_layer: nn.Module, r: int = 0, alpha: int = 1, dropout: float = 0.0):
super().__init__()
self.base_layer = base_layer
self.r = r
self.alpha = alpha
self.scaling = alpha / r
if isinstance(base_layer, nn.Linear):
self.lora_A = nn.Linear(base_layer.in_features, r, bias=False)
self.lora_B = nn.Linear(r, base_layer.out_features, bias=False)
else:
raise ValueError("Only nn.Linear is supported for base_layer")
self.dropout = nn.Dropout(p=dropout)
self.reset_parameters()
def reset_parameters(self):
nn.init.kaiming_uniform_(self.lora_A.weight, a=math.sqrt(5))
nn.init.zeros_(self.lora_B.weight)
def forward(self, x: torch.Tensor) -> torch.Tensor:
result = self.base_layer(x)
lora_output = self.lora_B(self.lora_A(self.dropout(x)))
return result + lora_output * self.scaling
class Linear(LoraLayer):
def __init__(self, in_features: int, out_features: int, r: int = 0, alpha: int = 1, dropout: float = 0.0):
base_layer = nn.Linear(in_features, out_features)
super().__init__(base_layer, r, alpha, dropout)
def add_lora_layers(model: nn.Module, r: int = 0, alpha: int = 1, dropout: float = 0.0):
for name, module in model.named_children():
if isinstance(module, nn.Linear):
setattr(model, name, Linear(module.in_features, module.out_features, r, alpha, dropout))
else:
add_lora_layers(module, r, alpha, dropout)
base_model = nn.Sequential(
nn.Linear(10, 20),
nn.ReLU(),
nn.Linear(20, 5)
)
add_lora_layers(base_model, r=4, alpha=16, dropout=0.1)
LoRA parameters
- LoRA alpha (
lora_alpha)- LoRA 업데이트의 강도를 조절하는 스케일링 팩터로, 원본 가중치와 LoRA 업데이트 사이의 균형을 조절
- 일반적으로 r과 같거나 더 큰 값을 사용
- 랭크 r (
r)- LoRA 행렬의 랭크, 즉 저차원 공간의 차원을 의미하는 상수로 모델의 적응 능력과 파라미터 효율성 사이의 트레이드오프를 결정
- 작은 r 값은 더 적은 파라미터를 의미하지만, 표현력이 제한될 수 있음 (본 논문에서는 1이나 2도 경쟁력있는 성능을 보였다고 보고)
- 스케일링 (
scaling)scaling = lora_alpha / r- LoRA 업데이트의 최종 크기를 결정하며, lora_alpha와 r의 비율에 따라 업데이트의 강도가 조절됨
- LoRA 드롭아웃 (
lora_dropout)- LoRA 레이어에 적용되는 드롭아웃 비율로 과적합을 방지
- 0.0이면 드롭아웃을 적용하지 않음
실제 LLM 트레이닝 사례
LoRA
# LoRA config
config = LoraConfig(
r=8,
lora_alpha=32,
target_modules=["q_proj","k_proj"], # We are only targetting the query and key attention layer
lora_dropout=0.01,
bias="none",
task_type="CAUSAL_LM"
)
# LoRA trainable version of the model
model = get_peft_model(model, config)
# trainable parameter count
model.print_trainable_parameters()
## trainable params: 3,407,872 || all params: 7,245,139,968 || trainable%: 0.04703666202518836
QLoRA
# Quantization Config
quant_config = BitsAndBytesConfig(
load_in_4bit=True,
bnb_4bit_quant_type="nf4",
bnb_4bit_compute_dtype=torch.float16,
bnb_4bit_use_double_quant=False
)
# Model
model = AutoModelForCausalLM.from_pretrained(
model_name,
quantization_config=quant_config,
device_map={"": 0}
)
model.config.use_cache = False
model.config.pretraining_tp = 1
학습 예시
# Load the tokenizer
tokenizer = AutoTokenizer.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1", use_fast=True, local_files_only=False, trust_remote_code=True)
# hyperparameters
lr = 2e-4
batch_size = 10
num_epochs = 2
# define training arguments
training_args = transformers.TrainingArguments(
output_dir= "mistral-ft",
learning_rate=lr,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
num_train_epochs=num_epochs,
weight_decay=0.01,
logging_strategy="epoch",
evaluation_strategy="epoch",
save_strategy="epoch",
load_best_model_at_end=True,
gradient_accumulation_steps=10,
warmup_steps=2,
fp16=True,
optim="paged_adamw_8bit",
)
# configure trainer
trainer = transformers.Trainer(
model=model,
train_dataset=tokenized_data["train"],
eval_dataset=tokenized_data["test"],
args=training_args,
data_collator=data_collator
)
# train model
model.config.use_cache = False
trainer.train()
# renable warnings
model.config.use_cache = True
본문
1 Introduction
사전 훈련된 언어 모델들은 GPT-2나 RoBERTa와 같이 이미 다양한 자연어 처리 작업에 적용되어 왔습니다. 특히 GPT-3와 같은 대규모 모델은 1750억 개의 훈련 가능한 파라미터를 포함하고 있어, 새로운 작업에 fine-tuning 할 때 많은 계산 자원과 저장 공간을 요구합니다. 이런 문제를 해결하기 위해, 일부 연구자들은 파라미터의 일부만 조정하거나 새로운 작업을 위한 외부 모듈을 학습하는 방법을 제안했습니다. 이런 방법들은 효율적인 작업 전환과 저장 공간 절약을 가능하게 하지만, 모델의 깊이를 증가시키거나 처리할 수 있는 시퀀스 길이를 줄이는 등의 문제를 유발할 수 있습니다.
2 Problem Statement
언어 모델링 작업에서는 주어진 문맥에 따른 조건부 확률을 최대화하는 것이 목표입니다. 예를 들어, 자연어 질의를 SQL 명령어로 변환(NL2SQL)하거나 문서 요약 같은 작업이 이에 해당합니다. 전통적인 full fine-tuning 방법은 사전 훈련된 모델의 모든 파라미터를 업데이트 하지만, 이는 파라미터의 크기가 큰 모델에서는 비효율적입니다. 따라서, 본 논문에서는 훨씬 적은 파라미터를 사용하는 저차원(Low-Rank) 표현을 사용하여 ∆Φ를 인코딩하는 방법을 제안합니다.
LoRA 접근 방식

사전 훈련된 모델의 가중치를 \(W \in \mathbb{R}^{d \times d}\)로 표현하며, 모델의 변형은 저차원 변환 \(A\)와 \(B\)를 통해 이루어집니다. 이때, \(A\)와 \(B\)는 각각 \(\mathcal{N}(0, \sigma^2)\)의 정규분포에서 추출됩니다. LoRA는 저차원 변환을 통해 학습을 진행하며, \(r\)이 작은 값 (e.g., 1 또는 2)이어도 충분히 효과적입니다. 변환된 가중치 \(\Delta W\)는 다음과 같이 계산됩니다.
\[\Delta W = A \times B^T\]이는 전체 모델 가중치 \(W\)에 대한 간단한 선형 변환을 의미하며, 이 변환은 기존의 가중치와 결합되어 fine-tuning 시 추가적인 인퍼런스 지연 없이 사용될 수 있습니다. LoRA 방법은 계산적으로도 메모리 측면에서도 효율적이며, 다양한 prior 방법과도 결합될 수 있습니다.
학습 시 이외에도 LFM 위에 fine-tuning(SFT + DPO)된 웨이트를 나누어서 관리하고 합쳐서 서빙하는 방법들이 주로 사용되고 있음.
이런 접근 방식은 전체 모델 fine-tuning과 비교하여, 학습해야 할 파라미터 수를 줄이면서도 모델의 성능을 유지할 수 있는 중요한 방법으로 자리잡고 있습니다.
3 Aren’t existing solutions good enough?
기존의 솔루션들은 대규모 모델에서 파라미터 효율성과 계산 효율성을 개선하기 위해 여러 방법들을 제시하였습니다. 언어 모델링을 예로 들면, 효율적인 어댑테이션을 위한 (1) 어댑터 레이어를 추가하는 것과 (2) 입력 레이어 활성화의 일부 쉐입을 최적화하는 전략으로 나뉩니다. 하지만, 이 두 전략 모두 대규모 및 지연시간에 민감한 생산 환경에서 제한적입니다.
-
Adapter Layers Introduce Inference Latency (어댑터 레이어가 인퍼런스 지연을 초래함)
어댑터 레이어는 파라미터가 적고 병목 차원이 작기 때문에 추가적인 FLOPs를 크게 증가시키지 않지만, 대규모 신경망은 하드웨어 병렬성을 필요로 하며, 어댑터 레이어는 순차적으로 처리되어야 합니다. 이는 온라인 인퍼런스 설정에서 배치 크기가 1인 경우에는 눈에 띄는 지연 증가를 유발할 수 있습니다. 또한, 모델을 분할할 필요가 있는 경우 추가적인 GPU 작업이 요구됩니다.
-
Directly Optimizing the Prompt is Hard (프롬프트의 직접 최적화는 어려움)
프리픽스 튜닝 같은 다른 접근 방식은 최적화가 어렵고 학습 가능한 파라미터에서 성능이 비모노토닉(비단조, non-monotonic)하게 변화한다는 것을 관찰했습니다. 또한, 적응을 위해 일부 시퀀스 길이를 예약함으로써 처리해야 할 downstream 작업의 시퀀스 길이가 감소하는 문제가 있습니다.
4 Method
4.1 저차원 파라미터화 업데이트 매트릭스 (Low-Rank-Parametrized Update Matrices)
신경망에는 많은 밀집층(dense layers)이 포함되어 있으며, 이런 층들은 행렬 곱셈을 수행합니다. LoRA는 사전 훈련된 가중치 매트릭스 \(W_0 \in \mathbb{R}^{d \times k}\)의 업데이트를 저차원 분해 \(W_0 + \Delta W = W_0 + BA\)로 제약하여, \(B \in \mathbb{R}^{d \times r}\)와 \(A \in \mathbb{R}^{r \times k}\)를 통해 표현하고, \(r\)은 \(\min(d, k)\)입니다. 훈련 중 \(W_0\)은 고정되며 그래디언트 업데이트를 받지 않습니다. 입력과 함께 두 행렬 \(W_0\)과 \(\Delta W = BA\)가 곱해지며, 그 결과 벡터들이 좌표별로 합산됩니다.
\[h = W_0x + \Delta Wx = W_0x + BAx \tag{3}\]이 방식은 전체 파인튜닝을 일반화한 쉐입이며, LoRA를 적용하면 모든 가중치 행렬에 대해 전체 파인튜닝의 표현성을 대략적으로 복원할 수 있게됩니다. 배포 시 추가적인 인퍼런스 지연 없이 \(W = W_0 + BA\)를 계산하여 저장할 수 있으며, 다른 downstream 작업으로 전환할 때 \(W_0\)을 \(BA\)를 빼고 다른 \(B_0A_0\)를 더함으로써 빠르게 수행할 수 있습니다.
4.2 트랜스포머에 LoRA 적용하기 (Applying LoRA to Transformer)
트랜스포머 아키텍처 내에서 LoRA를 적용할 수 있는 여러 가중치 매트릭스가 있습니다. 이 연구에서는 주로 어텐션 가중치에 초점을 맞추고 있으며, MLP 모듈은 훈련에서 제외하고 있습니다. 이는 간소화와 파라미터 효율성을 위함입니다. LoRA의 적용은 메모리 및 저장 사용을 크게 줄이며, 훈련 시 GPU 수를 줄이고 I/O 병목 현상을 피할 수 있도록 합니다. LoRA는 또한 훈련 중 25%의 속도 향상을 제공하며, 대다수의 파라미터에 대한 그래디언트 계산이 필요 없기 때문입니다.
5 Emperical Experiment
- RoBERTa, DeBERTa, GPT-2, GPT-3 모델을 다양한 NLU 및 NLG 작업에 대해 평가
- GLUE, WikiSQL, SAMSum 등 다양한 벤치마크를 사용하여 LoRA의 효율성 검증
- LoRA는 파라미터 효율성과 처리량에서 기존 fine-tuning 및 다른 어댑테이션 방법들을 능가함을 확인
5.1 실험 설계 및 베이스라인 설정
다양한 자연어 이해(NLU) 및 생성(NLG) 작업에 대해 LoRA를 평가하였습니다. 특히 RoBERTa와 DeBERTa 모델에 대해서는 GLUE 벤치마크를 사용했으며, GPT-2 및 GPT-3 모델은 WikiSQL과 SAMSum 데이터셋을 통해 평가되었습니다. NVIDIA Tesla V100을 모든 실험에 사용하였습니다.
베이스라인으로는 기존 연구에서 사용된 설정을 재현하여 가능한 한 많은 비교를 포함시켰으며, 베이스라인에는 전통적인 fine-tuning 방법뿐만 아니라 어댑터 레이어를 삽입하는 방법 등이 포함됩니다. 각 베이스라인의 성능은 GLUE 벤치마크를 통해 측정되었습니다.
모델 최적화 방법 상세 - Bias-only부터 LoRA까지
트랜스포머 모델은 입력 임베딩, 포지셔널 인코딩, 여러 층의 어텐션 및 FFN 네트워크, 그리고 출력 처리를 포함합니다. 각 층의 기본 구조는 다음과 같이 표현될 수 있습니다. ($\text{Sublayer}(x)$는 해당 층의 연산(e.g., 셀프 어텐션, FFN 네트워크)을 의미하고, $x$는 입력 벡터)
\[\text{LayerNorm}(x + \text{Sublayer}(x))\]위 기본적인 표현을 기반으로 각 모델 최적화 방안에 대해 살펴봅니다.
5.1.1 Bias-only 또는 BitFit
Bias-only 또는 BitFit은 딥러닝 모델에서 바이어스 벡터만 학습하고 나머지 가중치는 고정하는 최소화된 학습 접근 방식입니다.
\[\text{LayerNorm}(x + \textbf{W}x + \color{orange}{b})\]$\color{orange}{b}$는 학습되는 유일한 바이어스 벡터
모든 층의 바이어스 항에만 적용되며, 가중치 매트릭스는 고정
- 모델의 학습 가능한 파라미터 수를 줄이고, 바이어스를 조정함으로써 성능을 향상시키는데 초점을 맞춥니다.
- 각 뉴런의 출력에 고정된 오프셋을 추가하여, 결정 경계를 조정하고 모델의 예측 능력을 개선합니다. (바이어스 튜닝)
- 연구 사례: Zaken et al. (2021)에서는 이 방법이 비교적 단순함에도 불구하고 효과적일 수 있음을 입증하였습니다.
5.1.2 Prefix-embedding 튜닝 (PreEmbed)
\[x = \text{Embed}(x_{\text{original}} + \color{orange}{x_{\text{prefix}}})\]$\color{orange}{x_{\text{prefix}}}$는 추가된 특별 토큰의 임베딩
입력 임베딩 부분에 특별 토큰을 추가
입력 토큰 사이에 특별한 토큰을 삽입하여, 모델이 특정 작업에 더 잘 적응하도록 합니다.
- 토큰 유형: 학습 가능한 임베딩을 갖는 특별한 토큰을 사용합니다.
- 토큰 배치
- Prefixing: 입력의 시작 부분에 토큰을 추가
- Infixing: 입력의 중간에 토큰을 삽입
- 이런 토큰의 위치 조정에 따라 모델의 성능에 영향을 미칠 수 있음을 확인했습니다.
-
수식
\[|Θ_{preembed}| = d_{\text{model}} \times (l_p + l_i)\]
5.1.3 Prefix-layer 튜닝 (PreLayer)
\[\text{LayerNorm}(x + \color{orange}{\text{PreModifiedSublayer}(x)})\]$\color{orange}{\text{PreModifiedSublayer}(x)}$는 학습 가능한 활성화를 포함
각 층의 활성화 후 출력에 조정
Prefix-embedding 튜닝을 확장하여, 모든 Transformer 층 이후의 활성화를 학습 가능하게 만듭니다.
- 활성화 학습: 각 층의 출력 활성화를 학습 가능한 값으로 대체하여 모델이 입력에 대해 더 세밀하게 반응하도록 합니다.
-
수식
\(|Θ_{prelayer}| = L \times d_{\text{model}} \times (l_p + l_i)\) ($L$은 Transformer의 층 수)
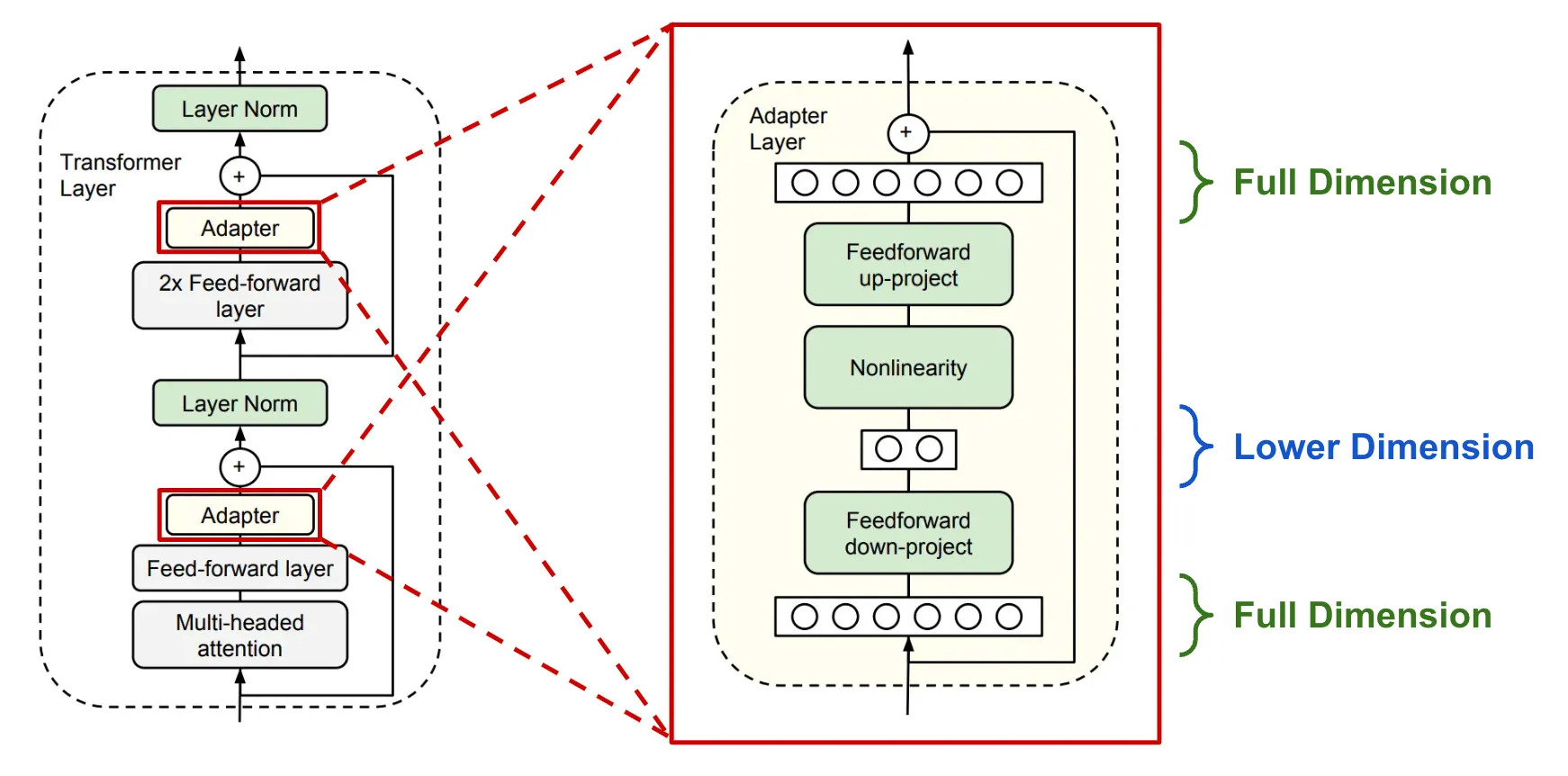
5.1.4 Adapter 튜닝
\[\text{LayerNorm}(x + \text{SelfAttention}(x) + \color{orange}{\text{Adapter}(x)})\]$\color{orange}{\text{Adapter}(x)}$는 추가된 어댑터 층의 출력
각 층의 어텐션과 FFN 사이에 어댑터 층을 삽입
기존의 모듈 사이에 추가적인 어댑터 층을 삽입하여 모델의 적응성을 향상시킵니다.
세부 설계 변형
- AdapterH: 전통적인 어댑터 설계, 비선형 활성화가 포함된 두 개의 완전 연결 층.
- AdapterL: MLP 모듈 후, LayerNorm 이후에만 어댑터 층을 적용합니다.
- AdapterP: AdapterL과 유사하나, 좀 더 최적화된 설계를 제공합니다.
- AdapterD: 효율을 위해 일부 어댑터 층을 제거합니다.
-
수식
\[|Θ_{adapter}| = L^{\text{Adpt}} \times (2 \times d_{\text{model}} \times r + r + d_{\text{model}}) + 2 \times L^{\text{LN}} \times d_{\text{model}}\]
5.1.5 LoRA (Low-Rank Adaptation)
상기 Adapter 튜닝 방식에 저차원 변환을 적용해 연산량을 줄이면서 웨이트를 업데이트(학습) → 성능 저하 거의 없고, 어댑터만 따로 분리해서 합치는 방식으로 인퍼런스 혹은 모델 웨이트 관리 가능
\[\text{SelfAttention}(x) = \text{softmax}\left(\frac{\color{orange}{(W_q + A_q)}Q \cdot (W_k + A_k)K^T}{\sqrt{d_k}}\right)(W_v + A_v)V\]$\color{orange}{A_q, A_k, A_v}$는 추가된 저순위 행렬
셀프 어텐션의 가중치 행렬에 저순위 행렬을 추가
기존 가중치 행렬에 순위가 낮은 행렬 쌍을 추가하여, 모델의 표현력을 향상시키면서도 파라미터 수는 제한합니다.
- 주로 쿼리와 값 가중치 행렬($W_q$, $W_v$)에 적용되며, 순위 분해를 통해 복잡한 상호 작용을 단순화시키며, 효율적인 학습이 가능하도록 합니다.
-
수식
\[|Θ_{LoRA}| = 2 \times L^{\text{LoRA}} \times d_{\text{model}} \times r\]
이 방법들은 모두 사전 훈련된 대규모 언어모델을 특정 작업에 맞게 파인튜닝하는 다양한 접근 방식을 나타냅니다. 각 방법은 훈련 가능한 파라미터의 수와 위치를 다르게 설정하여 효율성과 성능 사이의 균형을 맞추려고 시도합니다. 선행 연구를 비롯한 본 LoRA 논문의 기법은 궁극적으로 전체 모델을 재훈련하는 것보다 계산 효율적이면서도 특정 작업에 대한 성능을 향상시키는 것을 목표로 합니다.
현재는 일부 리소스가 풍부한 메타, 마이크로소프트 등을 포함해 오픈/독점 모델들 대부분이 LoRA 혹은 QLoRA를 거의 대부분 적용 (2024-08)
5.2 RoBERTa Base/Large
RoBERTa는 BERT의 훈련 레시피를 최적화하여 태스크 성능을 향상시킨 모델입니다. HuggingFace의 Transformers 라이브러리를 통해 RoBERTa base (125M)와 RoBERTa large (355M) 모델을 활용하여 GLUE 벤치마크에서 다양한 효율적인 어댑테이션 방법의 성능을 평가했습니다. LoRA의 평가를 위해 동일한 배치 크기와 시퀀스 길이를 사용하여 어댑터 베이스라인과의 비교를 공정하게 수행했습니다. 모델 초기화는 MRPC, RTE, STS-B에 대해 사전 훈련된 모델을 사용하고 MNLI에 이미 적응된 모델을 사용하지 않았습니다.
로버타(RoBERTa)와 데버타(DeBERTa) 모델을 포함한 다양한 어댑테이션 방법의 성능을 GLUE 벤치마크를 통해 평가했습니다. LoRA는 기존 방법들에 비해 높은 성능을 보였으며, 특히 작은 수의 훈련 가능한 파라미터를 사용함에도 불구하고 효율적인 성능을 보였습니다.
\[W_0 + \Delta W = W_0 + BA\]- \(W_0\)는 사전 훈련된 가중치 행렬
- \(\Delta W\)는 변경되는 가중치의 저차원 표현
- \(B\)와 \(A\)는 훈련 가능한 저차원 매트릭스
LoRA는 이런 저차원 분해를 통해 전체 모델의 파라미터 수를 줄이면서도 성능을 유지할 수 있습니다. 이는 복잡한 어댑테이션 과정을 간소화하며, 추가적인 인퍼런스 지연을 도입하지 않고 기존의 fine-tuning의 표현력을 대략 복원할 수 있습니다.
LoRA를 통한 실험 결과는 기존 fine-tuning 및 다른 어댑테이션 방법들과 비교하여 상당한 성능 향상을 보였습니다. 이는 LoRA가 파라미터 효율성과 처리량 측면에서 유망한 접근 방법임을 시사합니다. 추가적으로, 다양한 작업에 대한 어댑테이션 과정에서의 메모리 사용 감소와 훈련 효율성 증대는 실제 배포 시에 큰 이점을 제공합니다.
5.3 DeBERTa XXL
DeBERTa는 BERT의 변형으로, 더 큰 스케일에서 훈련되어 GLUE 및 SuperGLUE 벤치마크에서 경쟁력 있는 성능을 보였습니다. LoRA를 통해 완전한 파인튜닝을 한 DeBERTa XXL (1.5B) 모델과의 성능을 GLUE 벤치마크에서 비교했습니다.
5.4 GPT-2 Medium/Large
LoRA가 NLU 모델에서 경쟁력 있는 대안으로 확인된 후, NLG 모델인 GPT-2 medium 및 large에서도 LoRA의 우위를 검증하고자 했습니다. 설정은 Li & Liang (2021)의 연구와 최대한 일치하게 유지했습니다. E2E NLG Challenge에서의 결과만을 보고하며, 자세한 결과는 WebNLG와 DART에서 확인할 수 있습니다.
결론적으로 LoRA는 기존의 파인튜닝 및 다른 어댑테이션 방법에 비해 향상된 성능을 보였고, LoRA가 특히 파라미터 수가 많은 대규모 모델에서 효율적으로 작동할 수 있음을 의미합니다. LoRA를 사용하면 각종 NLU 및 NLG 작업에 걸쳐 모델의 적응성을 향상시킬 수 있으며, 더 낮은 비용으로 더 높은 성능을 달성할 수 있었다고 보고합니다.
6 관련 연구
본 연구에서는 Transformer 언어 모델들의 발전과 그 응용에 대해 논의합니다. Transformer는 self-attention을 집중적으로 사용하는 sequence-to-sequence 아키텍처입니다(Vaswani et al., 2017). 이후, Radford et al.은 autoregressive 언어 모델링을 위해 Transformer 디코더 스택을 사용하였습니다. 이런 Transformer 기반 언어 모델들은 NLP 분야에서 많은 작업에서 최고의 성능을 보여주고 있습니다. 특히, BERT (Devlin et al., 2019b)와 GPT-2 (Radford et al., b)는 대량의 텍스트 데이터에 대한 사전 훈련 후, 특정 작업 데이터에 대한 파인튜닝을 통해 성능을 크게 향상시킬 수 있는 새로운 패러다임을 제시했습니다. 이런 큰 모델들은 일반적으로 더 큰 성능을 내며, GPT-3 (Brown et al., 2020)는 현재까지 훈련된 가장 큰 단일 Transformer 언어 모델로, 1750억 개의 파라미터를 갖고 있습니다.
7 LoRA(Low-Rank Adaptation)의 특성 이해
저차원(Low-Rank) 업데이트는 특히 GPT-3 175B 모델에서 실시된 연구를 중심으로, 이런 업데이트가 어떻게 효율적으로 구현되고, 어떤 이점을 제공하는지를 분석합니다. 저차원 구조는 하드웨어 요구사항을 낮추며, 업데이트된 가중치가 사전 훈련된 가중치와 어떻게 연관되어 있는지에 대해 더 나은 해석을 가능하게 합니다. 이런 연구는 다음과 같은 질문에 답하기 위해 수행됩니다.
LoRA는 큰 언어 모델을 효율적으로 파인튜닝하는 방법입니다. 이 연구에서는 GPT-3 175B 모델을 중심으로 LoRA의 특성을 분석했습니다.
- 어떤 가중치 행렬을 적응시켜야 할까?
- 적응 행렬의 최적 랭크는 얼마일까?
- 적응 행렬($\Delta W$)과 원래 가중치($W$)의 관계는 어떨까?
7.1 어떤 가중치 행렬을 적응시켜야 할까? (Which weight matrices in Transformer should we apply LoRA to?)
사전 훈련된 Transformer에서 어떤 가중치 매트릭스를 LoRA를 적용해야 최대의 성능을 발휘하는가에 대한 연구입니다. 연구 결과, self-attention 모듈 내의 가중치($W_q$, $W_v$)를 선택하는 것이 최적의 결과를 도출합니다(Section 7.1).
| 가중치 타입 | $W_q$ | $W_k$ | $W_v$ | $W_o$ | $W_q$, $W_k$ | $W_q$, $W_v$ | $W_q$, $W_k$, $W_v$, $W_o$ |
|---|---|---|---|---|---|---|---|
| 랭크 $r$ | 8 | 8 | 8 | 8 | 4 | 4 | 2 |
| WikiSQL | 70.4 | 70.0 | 73.0 | 73.2 | 71.4 | 73.7 | 73.7 |
| MultiNLI | 91.0 | 90.8 | 91.0 | 91.3 | 91.3 | 91.3 | 91.7 |
결과적으로 $W_q$와 $W_v$를 함께 적응시키는 것이 가장 좋은 성능을 보였습니다. 이는 낮은 랭크($r=4$)로도 충분한 정보를 포착할 수 있음을 시사합니다.
권고: $W_q$와 $W_v$에 적용 (QLoRA에서 이 권고를 따르고, 대부분 이 권고를 따름.)
7.2 최적의 Rank 결정(What is the optimal rank $r$ for LoRA?)
LoRA를 적용할 때 사용하는 rank의 크기가 모델 성능에 미치는 영향을 조사합니다. 실험 결과, 작은 rank(e.g., $r = 1$)만으로도 $W_q$와 $W_v$에 LoRA를 적용할 때 충분히 경쟁력 있는 성능을 나타냅니다(Section 7.2).
다양한 랭크($r$)에 대해 실험한 결과 작은 $r$ 값으로도 경쟁력 있는 성능을 보였습니다.
| 가중치 타입 | $r = 1$ | $r = 2$ | $r = 4$ | $r = 8$ | $r = 64$ |
|---|---|---|---|---|---|
| WikiSQL: $W_q$ | 68.8 | 69.6 | 70.5 | 70.4 | 70.0 |
| WikiSQL: $W_q$, $W_v$ | 73.4 | 73.3 | 73.7 | 73.8 | 73.5 |
| WikiSQL: $W_q$, $W_k$, $W_v$, $W_o$ | 74.1 | 73.7 | 74.0 | 74.0 | 73.9 |
| MultiNLI: $W_q$ | 90.7 | 90.9 | 91.1 | 90.7 | 90.7 |
| MultiNLI: $W_q$, $W_v$ | 91.3 | 91.4 | 91.3 | 91.6 | 91.4 |
| MultiNLI: $W_q$, $W_k$, $W_v$, $W_o$ | 91.2 | 91.7 | 91.7 | 91.5 | 91.4 |
이는 적응 행렬 $\Delta W$가 작은 “내재적 랭크”를 가질 수 있음을 시사합니다.
$\Delta W$와 $W$ 사이의 상관 관계 및 $\Delta W$의 크기를 $W$와 비교하여 분석합니다. $\Delta W$는 $W$의 특정 상위 singular 방향들을 강조하여, 이를 통해 특정 downstream 작업에 중요한 특징들을 증폭시키는 것으로 나타났습니다(Section 7.3).
서로 다른 $r$ 값으로 학습된 적응 행렬 간의 부분공간 유사도를 분석했습니다. 유사도는 다음 수식으로 계산됩니다.
\[\phi(A_{r=8}, A_{r=64}, i, j) = \frac{||U^i_{A_{r=8}}{}^TU^j_{A_{r=64}}||^2_F}{\min(i, j)} \in [0, 1]\]분석 결과, $r=8$과 $r=64$의 상위 특이벡터 방향이 상당히 겹치는 것을 발견했습니다. 특히 $\Delta W_v$와 $\Delta W_q$에서 상위 1개 방향의 정규화된 유사도가 0.5 이상으로 나타났습니다.
$r$은 대다수의 모델 파라미터 수와 목적에 따라 다양하게 사용하는 편임.
7.3 가중치 매트릭스 비교(How does the adaptation matrix ∆W compare to W?)
$\Delta W$와 $W$의 관계를 조사하기 위해 $W$를 $\Delta W$의 $r$차원 부분공간에 투영했습니다. 적응 행렬 $\Delta W$와 $W$의 관계분석 결과는 다음과 같습니다.
| $r = 4$ | $\Delta W_q$ | $W_q$ | Random |
|---|---|---|---|
| $|U^TW_qV^T|_F$ | 0.32 | 21.67 | 0.02 |
| $|W_q|_F$ | 61.95 | - | - |
| $|\Delta W_q|_F$ | 6.91 | - | - |
| $r = 64$ | $\Delta W_q$ | $W_q$ | Random |
|---|---|---|---|
| $|U^TW_qV^T|_F$ | 1.90 | 37.71 | 0.33 |
| $|W_q|_F$ | 61.95 | - | - |
| $|\Delta W_q|_F$ | 3.57 | - | - |
이 결과로부터 다음과 같은 결론을 도출할 수 있습니다.
- $\Delta W$는 $W$와 무작위 행렬보다 더 강한 상관관계를 가진다.
- $\Delta W$는 $W$의 상위 특이방향을 반복하는 대신, $W$에서 강조되지 않은 방향을 증폭시킨다.
- 증폭 비율은 상당히 큰 편이다. ($r=4$일 때 약 21.5배)
8 결론 및 향후 연구 방향
본 논문에서는 거대 언어 모델의 파인튜닝이 요구하는 고비용의 하드웨어와 다양한 작업을 위한 독립된 인스턴스의 호스팅 및 전환 비용을 고려하여, LoRA라는 효율적인 적응 전략을 제안하였습니다. LoRA는 인퍼런스 지연을 도입하지 않고 입력 시퀀스 길이를 감소시키지 않으면서도 높은 모델 품질을 유지하는 전략입니다. 특히, 서비스로 배포될 때 대부분의 모델 파라미터를 공유함으로써 빠른 작업 전환을 가능하게 합니다. 이 연구는 Transformer 언어 모델에 초점을 맞추었지만, 제안된 원칙은 밀집층을 갖는 어떠한 신경망에도 일반적으로 적용될 수 있습니다.
향후 연구 방향은 다음과 같습니다.
- 효율적 적응 방법 결합: LoRA는 다른 효율적인 적응 방법들과 결합될 수 있으며, 이는 서로 직교하는 개선을 제공할 수 있습니다.
- 파인튜닝 및 LoRA의 메커니즘: 파인튜닝 또는 LoRA가 어떻게 사전 훈련 동안 학습된 특징들을 변형시켜 downstream 작업에서 성공적으로 작동하게 하는지에 대한 메커니즘은 아직 명확하지 않습니다. LoRA는 전체 파인튜닝보다 이런 질문에 접근하기 더 용이할 것입니다.
- 가중치 매트릭스 선택의 원칙: 현재 LoRA를 적용할 가중치 매트릭스를 선택하는 데 주로 휴리스틱을 의존하고 있습니다. 이를 수행하는 더 원칙적인 방법이 있을까요?
- $\Delta W$의 등급 결핍성: $\Delta W$의 등급 결핍성은 $W$ 또한 등급 결핍일 수 있다는 가능성을 제시하며 추가적인 탐색이 필요함을 언급합니다.
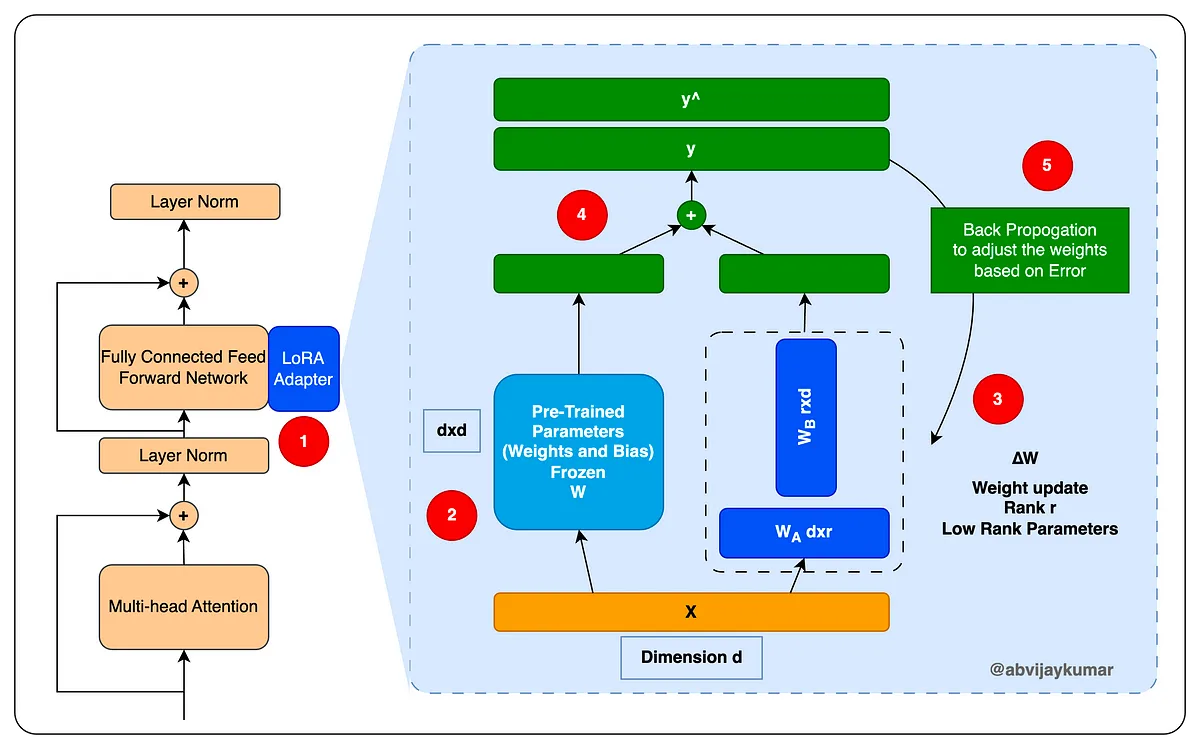 *출처:
*출처: