Lean GitHub**

• Related Project: Private
• Category: Paper Review
• Date: 2024-07-25

LEAN-GitHub: Compiling GitHub LEAN repositories for a versatile LEAN prover

• url: https://arxiv.org/abs/2407.17227
• pdf: https://arxiv.org/pdf/2407.17227
• homepage: https://lean-lang.org/
• github: https://github.com/leanprover/lean4
• vsc: https://marketplace.visualstudio.com/items?itemName=leanprover.lean4
• theorem-proving-in-lean4: https://lean-lang.org/theorem_proving_in_lean4/introduction.html
• abstract: Recently, large language models have presented promising results in aiding formal mathematical reasoning. However, their performance is restricted due to the scarcity of formal theorem-proving data, which requires additional effort to be extracted from raw formal language corpora. Meanwhile, a significant amount of human-written formal language corpora remains underutilized. To address this issue, we propose LEAN-GitHub, a dataset consisting of large-scale formal data extracted from almost all Lean 4 repositories on GitHub. After fine-tuning InternLM-math-plus on this dataset, our model achieved accuracies of 48.8% with a single pass and 54.5% with 64 passes on the Lean 4 miniF2F test, surpassing state-of-the-art method at 52%. And it also achieves state-of-the-art on two other Lean 4 benchmarks (ProofNet and Putnam) targeting different fields/levels of math. These results demonstrate that our proposed dataset is beneficial for formal reasoning on a wide range of math topics. We open-source our model at https://GitHub. com/InternLM/InternLM-Math and our data at this https URL datasets/InternLM/Lean-GitHub

수정 중 초고

TL;DR

• 본 논문에서는 LEAN-GitHub 데이터셋을 소개하며, 이를 통해 효율적으로 수학적 정리를 증명하는 능력을 높임.
• 대규모 Lean 저장소에서 추출한 공식 데이터를 활용하여 InternLM2-StepProver 모델을 훈련함.
• 향상된 정리를 증명하는 능력은 다양한 수학 분야에서 향상된 벤치마크 결과를 보여줌.

(사견) 주요 성과는 데이터 전처리와 그로 견인한 성능 향상정도지만 많은 도메인에서 필요한 일이라서 큰 관심을 받은 것이 아닐까하는 생각을 해보았습니다.

(사견) 토크나이저처럼 사람이 이해하는 것과 동일하게 제대로 정리해서 임베딩해야한다. 제대로 규칙적으로 컴파일하고, CoT와 같이 차근히 논증적으로 토큰(언어, 수학)의 연결성을 학습시켜야한다. 정형화된 포맷으로 데이터 처리 및 모델에 인코딩 혹은 임베딩하며 제대로 전달하는 것이 중요하다.

이 논문은 자동 정리 증명의 현황과 데이터셋의 부족 문제를 해결하기 위한 새로운 접근 방식을 제시합니다. 특히, LEAN-GitHub라는 새로운 데이터셋을 도입하고 이를 사용하여 형식적 인퍼런스 능력을 향상시키는 방법을 탐구합니다.

[데이터 퀄리티 및 정형화(e.g,형식 강조 emd) 색인마킹]

[문제 정의와 동기]

• 문제 정의: 현대 수학에서는 정리 증명의 복잡성 증가로 인해, 오류 식별이 어려워지고 있습니다. 이를 해결하기 위해 다양한 형식화된 수학적 시스템이 개발되었으나, 이런 시스템들은 대부분 상당한 휴먼의 노력을 필요로 합니다.
• 동기 부여: 기존의 데이터 부족 문제를 해결하고, 자동화된 정리 증명의 효율을 향상시키기 위해, 본 논문에서는 GitHub의 오픈 소스 Lean 저장소를 활용한 새로운 데이터셋, LEAN-GitHub을 제안합니다. 이 데이터셋은 기존 Mathlib 데이터셋을 보완하여 훈련 데이터의 질과 다양성을 크게 향상시키는 것을 목표로 합니다.

[기존 연구와의 연결]

• 형식 시스템의 발전: Coq, Isabelle, Lean 등의 형식 시스템 발전으로 인해 자동 정리 증명(일부는 증명 보조 툴임)에 대한 관심이 높아졌습니다. 이 시스템들은 표현력이 풍부하고 정교한 증명을 가능하게 하지만, 사용하기 위해서는 고도의 전문성이 요구됩니다. (메디컬 혹은 다른 도메인에서 직면한 문제와 비슷)
• 자동 정리 증명(ATP): 초기의 ATP 연구는 주로 전통적인 알고리즘을 사용했으나, 최근에는 대규모 언어모델과 심층 트랜스포머를 활용하여 정리들을 처리하는 방식이 등장했습니다. 이런 접근 방식은 전술 생성과 같은 복잡한 문제를 해결할 수 있는 능력을 제공합니다.

[데이터셋 구축 과정]

• 데이터셋의 필요성: 기존의 데이터셋들은 주로 단순화된 문제나 제한된 범위의 문제에 초점을 맞추고 있어, 현실 세계의 복잡한 수학적 문제를 해결하는 데는 부적합했습니다. LEAN-GitHub은 이런 한계를 극복하고자 합니다.
• 데이터 추출 및 처리: 다양한 GitHub 저장소에서 수학적 증명과 정리들을 추출하여, 형식적 인퍼런스 훈련에 적합한 형태로 변환하는 복잡한 과정을 설명합니다. 이 과정은 증명의 중간 상태나 전술 정보 등을 포함하여 데이터의 풍부함을 보장합니다.

[데이터셋의 효과 검증]

• 실험 설계: InternLM2-StepProver 모델을 사용하여 LEAN-GitHub 데이터셋의 효과를 다양한 벤치마크를 통해 검증합니다. 이 모델은 복잡한 수학적 인퍼런스과 정리 증명을 수행할 수 있는 능력을 갖추고 있습니다.
• 결과 및 분석: LEAN-GitHub을 통해 훈련된 모델은 기존 모델들보다 더 높은 정확도와 성능을 보여주며, 특히 고등학교 수준 이상의 문제에서 향상된 결과를 달성합니다.

[연구의 기여와 미래 전망]

• 연구 기여: 본 논문은 LEAN-GitHub 데이터셋의 개발과 이를 활용한 형식적 인퍼런스 능력 향상을 통해 자동 정리 증명 분야에 중요한 기여를 합니다.
• 미래 전망: 데이터셋의 공개를 통해 연구 커뮤니티가 더 많은 형식적 데이터를 활용하여, 더 복잡하고 다양한 수학적 문제를 해결할 수 있기를 기대합니다. 이를 통해, 형식적 증명의 자동화와 데이터 기반 접근 방식의 발전, 실제 수학적 문제 해결에 큰 진전을 이루는 데 기여할 수 있을 것이라고 언급합니다.

1 서론

정리 증명은 수학에서 기본적인 목표로 증명의 복잡성이 증가함에 따라 비직관적인 오류를 식별하기 위해, Lean [6], Isabelle [19], Coq [24]과 같은 형식화된 수학적 시스템이 개발되었습니다. 이런 시스템은 컴퓨터로 검증 가능한 증명 방식을 제공합니다 [2].

그러나 형식적 증명을 구성하는 데는 상당한 휴먼의 노력이 요구되며, 이는 추가 발전에 있어 챌린지를 제시하고 자동화된 정리 증명의 필요성을 강조합니다 [18]. 최근에는 대규모 언어모델들(LLMs) [1, 4, 34, 21, 23, 9, 26, 36]이 고등학교 수준의 수학 문제를 해결하는 데 있어 유망한 결과를 보였으며, 형식화된 증명 보조자와의 상호작용을 통해 이루어졌습니다. 그럼에도 불구하고, 이들의 성능은 주로 데이터 부족으로 인해 만족스럽지 못합니다.

형식 언어는 상당한 전문 지식과 노력을 필요로 하며, 비교적 적은 수의 수학자에 의해 사용됩니다.

이로 인해 (1) 형식 언어 코퍼스의 부족 문제가 있고, 파이썬이나 자바와 같은 전통적인 프로그래밍 언어와 달리, 형식 증명 언어의 원시 코드에는 (2) 직접적으로 보이지 않는 중간 정보를 포함하고 있습니다. 예를 들어, 증명 단계 사이의 중간 상태를 포함하는 증명 트리 등이 이에 해당합니다. 이로 인해 원시 언어 코퍼스는 훈련에 적합하지 않으며, 가치 있는 휴먼이 작성한 코퍼스들은 여전히 온전히 활용되지 못하고 있습니다.

비록 자동 형식화 [30, 35]가 훈련을 위한 더 정렬된 데이터의 합성을 가능하게 하지만, 데이터의 질과 다양성은 제한적이며, 휴먼이 작성한 데이터를 대체할 수 없습니다.

이런 챌린지를 해결하기 위해, 본 논문에서는 GitHub의 오픈 소스 Lean 저장소를 활용하는 대규모 Lean 데이터셋인 LEAN-GitHub을 제안합니다. 이는 잘 활용되고 있는 Mathlib [17, 34] 데이터셋을 중요하게 보완합니다. 추출 효율과 병렬성을 증진시키기 위한 확장 가능한 파이프라인을 개발했으며, 이전에 컴파일되고 추출되지 않았던 Lean 코퍼스에서 귀중한 데이터를 활용할 수 있었습니다. 또한, 트리 증명 검색 방법에서 흔히 발생하는 상태 중복 문제에 대한 해결책을 제공합니다. 데이터셋을 포함하여 훈련된 InternLM2-StepProver 모델의 효과를 보여주기 위해, 다양한 형식 벤치마크에서 Lean 4의 형식적 인퍼런스 능력을 향상시키는 결과를 양적으로 보여줍니다. 이는 제안한 데이터셋이 다양한 수학 주제에서 형식적 인퍼런스에 유익함을 시사합니다.

본 논문은 다음과 같은 기여를 합니다.

• 대규모 형식 데이터를 포함하는 LEAN-GitHub 데이터셋을 공개적으로 릴리스합니다. 이 데이터셋은 GitHub에서 Lean 4 저장소로부터 추출되며, 자동 정리 증명의 추가적 연구 및 개발을 촉진합니다.
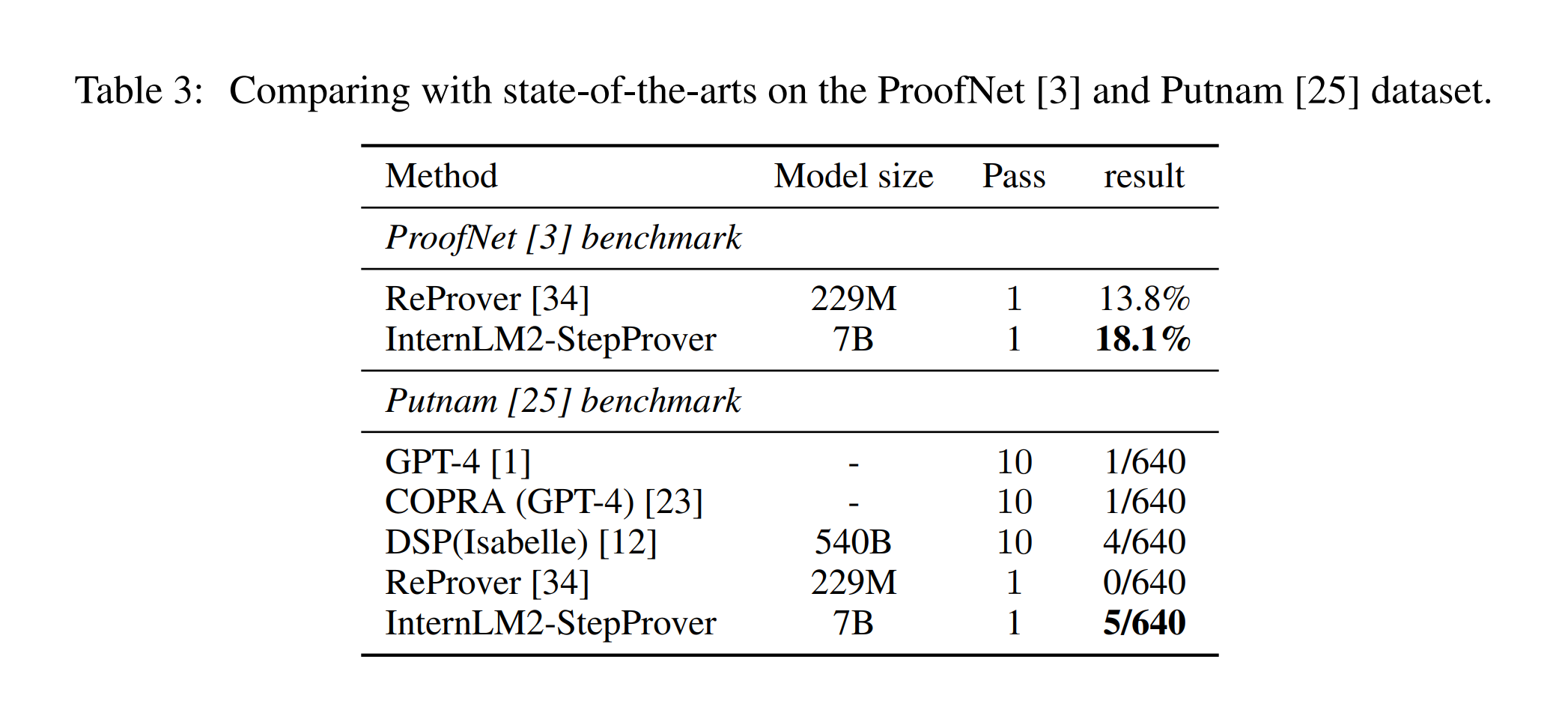
• 이 데이터셋으로 훈련된 7B 크기의 InternLM2-StepProver 모델은 다양한 수학 분야/수준의 벤치마크에서 최고의 성능을 달성하였습니다. InternLM2-StepProver는 Lean 4 miniF2F [38] 테스트에서 단일 패스에서 48.8%, 64 패스에서 54.5%의 정확도를 보고했습니다. 이는 Deepseek-Prover [30]의 52%를 능가하는 것입니다; ProofNet [3]에서 18.1% Pass@1을 기록하였으며, Putnam [25] 문제 중 5개를 해결하였습니다. 추가로, 모델은 miniF2F 데이터셋에서 3개의 IMO 문제를 해결하였습니다(예시는 Figure 1 참조).

2 관련 연구

현대의 증명 보조 도구들, Coq [24], Isabelle [19], Lean [6]의 발전은 일차 논리를 넘어서는 형식 시스템의 표현력을 확장하였습니다. 이는 자동 정리 증명에 대한 관심을 증대시켰습니다. 최근에는 대규모 언어모델 [1, 4, 22, 30, 36]이 도구 및 데이터셋 개발을 더욱 발전시키는 데 기여하였습니다.

• 관련 연구에서는 형식 시스템, 자동 정리 증명, 데이터 추출 기술에 대한 발전을 다룸.
• 다양한 접근 방식을 통해 정리 증명의 자동화를 추구하며, 효과적인 데이터셋 구축에 중점을 둠.
• 최신 언어 모델과 데이터 추출 도구를 활용하여 새로운 데이터셋을 구성하고 성능 개선을 목표로 함.

자동 정리 증명(ATP)

초기의 ATP 연구들은 KNN [8]이나 GNN [32]과 같은 전통적인 방법을 사용하였습니다. 일부 연구 [13, 5, 28]는 성능 향상을 위해 강화 학습 기술을 활용하였습니다. 최근에는 정리들을 일반 텍스트로 처리하는 심층 트랜스포머 기반 방법들이 점차 활용되고 있습니다. 많은 학습 기반 정리 증명 방법들, 예를 들어 GPT-f [21], PACT [9], Llemma [4], COPRA [23], ReProver [34], Lean-STaR [16]은 (증명 상태, 다음 전술) 쌍에 언어 모델을 지도하고, 트리 검색을 통해 정리를 증명합니다. 일부는 추상 구문 트리의 세분성에서 전술을 생성하는 방법을 시도합니다 [32]. 다른 대안으로는, LLM들을 사용하여 전적으로 독립적으로 혹은 휴먼이 제공한 증명을 기반으로 전체 증명을 자동으로 생성하는 방법이 포함됩니다 [30, 7, 37, 12, 31]. 또한, 비공식 증명을 공식 증명에 통합하는 가능성을 탐구하는 방법들도 있습니다 [12, 29, 16, 26].

Lean 코퍼스를 위한 데이터 추출

증명 보조자와 상호작용하는 휴먼의 행동을 모방하여, 자동 정리 증명기가 코드에서는 보이지 않지만 실행 시 휴먼에게 보이는 중간 상태를 볼 수 있어야 합니다. 따라서 데이터 추출 도구는 ATP의 중요한 동력입니다. Coq은 GamePad [11] 및 CoqGym [33]을 가지고 있고, Isabelle은 IsarStep [15]를, Lean은 LeanStep [9], leangym [20] (Lean 4와 호환되지 않음) 및 LeanDojo [34]를 갖고 있습니다. Lean 4를 위한 추출 도구에 중점을 둡니다. 그러나 이전 Lean 4 도구들은 단일 프로젝트를 위해 설계되어 대규모 추출에 직접적으로 적합하지 않은 상당한 추출 오버헤드를 포함합니다.

3. GitHub-Lean Dataset

GitHub에는 많은 Lean 저장소가 존재하며, 이들 중 많은 것들이 드물게 휴먼이 작성한 정리와 증명을 포함하고 있습니다. 그러나 원시 Lean 코드는 직접 훈련에 적합하지 않습니다. 예를 들어, 각 증명 단계 사이의 중간 상태와 목표, 일부 전술에 의해 제공되는 힌트 등이 포함되어 있습니다. 이런 정보를 추출하는 작업이 있었으나, 이는 Mathlib 4 [34, 17]에 제한되어 있었습니다. 한편, GitHub에는 다양한 주제를 다루는 수백 개의 Lean 저장소가 있지만 활용되거나 추출되지 않고 있습니다. 147개의 Lean 4 저장소를 기반으로 하여 LEAN-GitHub이라는 데이터셋을 형성하였습니다. 이 데이터셋은 Lean 4 공식 수학에서 가장 큰 정리 증명 데이터셋 중 하나로, 28,597개의 정리와 공식 증명, 218,866개의 전술을 2,133개 파일에서 포함하고 있습니다. 데이터셋은 0.138B 토큰을 갖고 있습니다. 데이터셋 훈련을 통한 모델 성능 개선이 다양한 수학 주제에서의 정리 증명에 도움이 될 것이라고 제안합니다.

3.1 데이터셋 구축

저장소 선택 GitHub에서 철저한 검색을 수행한 후, 총 237개의 Lean 4 저장소(Lean 3과 Lean 4를 구분하지 않음)를 식별했으며, 이들 중 컴파일 가능한 정리가 포함될 수 있습니다. “theorem”과 “lemma”와 같은 키워드를 필터링하여, 이들 저장소에서 약 48,091개의 정리가 있는 것으로 추정됩니다. 그러나 키워드의 존재가 전술 형식으로 작성된 정리의 존재를 보장하지는 않습니다. 주요 장애물로는 일부 저장소가 컴파일할 수 없거나 온라인으로 사용할 수 없는 다른 저장소에 의존하거나 이전 버전의 Lean으로 작성되어 새 버전으로 마이그레이션할 수 없거나 전술을 사용하여 구성되지 않은 정리의 증명 등이 있습니다. 구식 버전의 Lean 4로 작성된 90개 저장소를 폐기하였습니다. 나머지 저장소 중에서는 수정 없이 유효한 Lean 4 프로젝트로 컴파일할 수 있는 저장소가 61개뿐이었습니다. 나머지 저장소는 성공적으로 컴파일하기 위해 추가 노력이 필요했습니다. 일부 프로젝트는 비공식 Lean 4 릴리스에 의존하고 있으며, 다른 일부는 상당한 수의 격리된 파일을 포함하고 있습니다. 전자의 경우에 가장 가까운 공식 릴리스를 경험적으로 찾아보는 자동 스크립트를 개발하였습니다. 후자의 경우에 대한 해결책은 다음 단락에서 설명합니다.

[소스 코드 컴파일]

Lean 4 표준 라이브러리에서 제공하는 Lake [6] 도구를 사용하지 않고, leanc 컴파일러를 직접 호출하여 소스 코드를 컴파일하기로 하였습니다. 이 접근 방식은 두 가지 장점을 제공합니다.

(1) 첫째, 수집된 많은 Lean 저장소는 호환되지 않는 Lean 프로젝트이며 컴파일할 수 없습니다. 이는 Lean 4가 컴파일 언어와 스크립트 언어로 모두 기능할 수 있기 때문입니다. 수학자들은 종종 빈 Lean 프로젝트 내에서 격리된 파일을 작성하는 경향이 있는데, 이는 Lake에 의해 컴파일될 수 없습니다.

(2) 둘째, Lake는 건물의 목표 중 하나라도 실패하면 프로젝트를 빌드하지 못하고 전체 프로젝트의 내용을 폐기하게 됩니다. Lake의 동시성 원시에 성능 병목 현상을 관찰하였습니다. 이 문제를 해결하기 위해, 먼저 Lake의 파일 의존성에 대한 가져오기 그래프를 확장하였습니다. 그런 다음 격리된 파일의 정보를 추가하여 글로벌 가져오기 그래프를 재구성하였습니다. 이 의존성 정보를 바탕으로, Lake를 병렬성이 증가된 사용자 정의 컴파일 스크립트로 대체할 수 있었습니다.

[추출 세부 정보]

LeanDojo [34]를 기반으로 추출 유틸리티를 개발하였습니다. LeanDojo [34] 및 LeanStep [9]과 같은 도구들은 일반적으로 데이터 추출 전에 전체 프로젝트를 컴파일해야 합니다. 이 제한이 필요 없다고 주장하며 격리된 파일에 대한 데이터 추출을 구현하였습니다. LeanDojo의 네트워크 연결에 대한 의존성과 데이터 추출 및 Lean과의 상호 작용을 함께 두는 설계 선택으로 인해 도입된 일부 병목 현상을 관찰하였습니다. 이런 계산상의 중복을 줄이기 위해, 병렬성을 증가시킨 구현으로 재구조화하였습니다. 8,639개의 Lean 소스 파일 중 6,352개 파일과 42K 정리가 성공적으로 추출되었으며, 2,133개 파일과 28K 정리는 유효한 전술 정보를 포함하고 있습니다.

3.2 데이터셋 통계

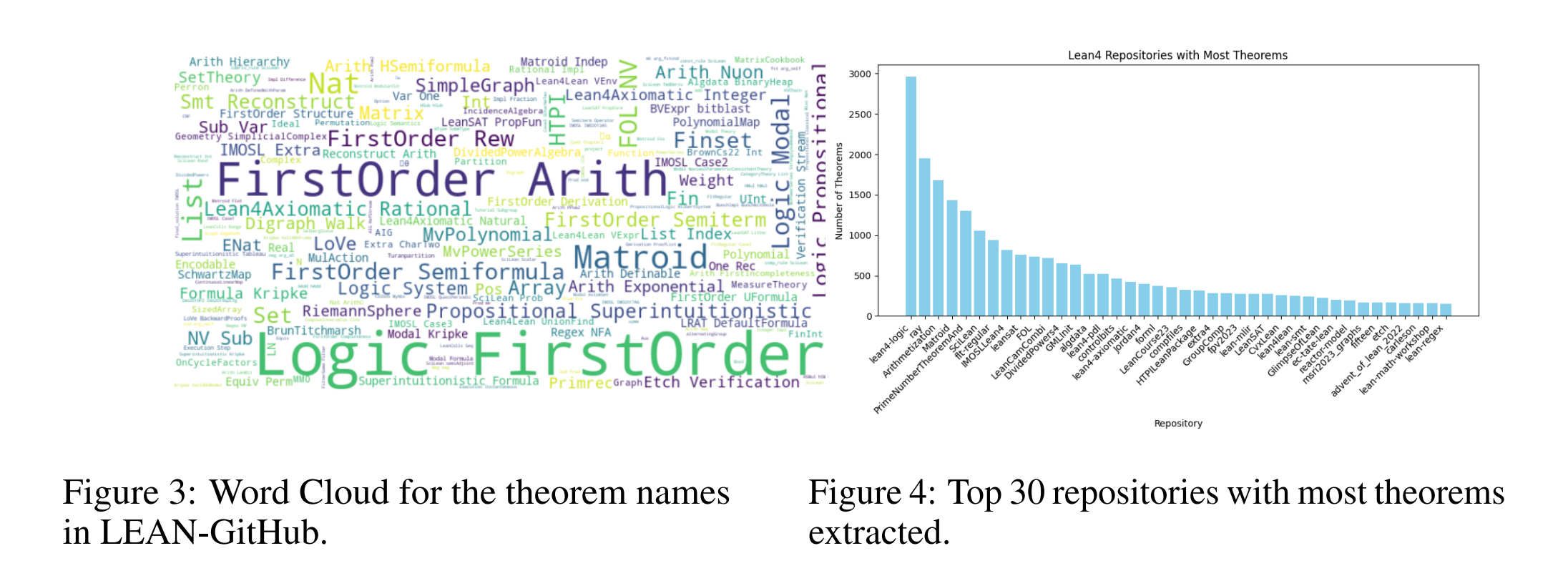
Figure 3은 데이터셋의 정리 이름 세트에서 가장 자주 발생하는 키워드를 강조하는 워드 클라우드를 보여줍니다. “Logic”, “FirstOrder”, “Matroid”, “Arith(mezation)”이 가장 두드러지며, 이는 데이터셋이 다양한 수학 분야를 포함하고 있음을 나타냅니다. Figure 4는 추출된 정리가 가장 많은 상위 30개 저장소를 표시합니다. 데이터의 분포는 SOTA 수학 분야, 데이터 구조, 올림피아드 수준의 문제를 포함한 다양한 수학 주제를 보여줍니다. 데이터셋의 품질을 추정하기 위해, 여러 양적 측정치를 제공하고 최근 및 유사한 기존 데이터셋, 즉 Lean-Workbook, Deepseek-Prover, miniF2F-curriculum 및 LeanDojo-Mathlib과 비교합니다(표 1 참조).

4 실험

• 본 실험에서는 LEAN-GitHub 데이터셋을 활용한 InternLM2-StepProver 모델을 개발하여 다양한 벤치마크에서 테스트하고, 모델의 효과를 검증함.
• 다양한 데이터셋 및 설정하에서 포괄적인 평가를 수행하고, 중복 상태 제거를 통해 계산 효율을 향상시키는 기술을 도입함.
• 주요 결과는 InternLM2-StepProver가 다양한 수준과 난이도의 문제에서 기존 방법들을 상회하는 성능을 보였음을 보여줌.

4.1 실험 설정

4.1.1 모델 및 훈련

InternLM2-StepProver 모델은 200B의 비공식 및 공식 수학 관련 토큰으로 구성된 코퍼스에서 사전 훈련된 InternLM-math-plus-7B [36] 모델을 기반으로 구축되었습니다. 훈련 세트는 주로 세 부분으로 구성됩니다. LEAN-GitHub, Lean의 Mathlib(LeanDojo 데이터셋을 통해), 그리고 자동 형식화 노력의 결과로 생성된 기타 개인적인 합성 정리들. 다양한 훈련 세트 설정으로 여러 모델이 훈련되었습니다. 훈련은 주어진 GOAL(현재 Lean 전술 상태)과 DECLARATION(증명되어야 할 Lean 정리 이름)에 대해 PROOFSTEP(Lean 전술)을 생성하는 proofstep 목표를 따랐습니다. 전역 배치 크기는 512, 학습률은 \(10^{-5}\)로 설정되었으며, 2 epoch 동안 파인튜닝하여 SFT 모델을 얻었습니다. 전체 파인튜닝 과정은 32개의 A100 GPU에서 약 6시간 동안 진행되었습니다.

4.1.2 평가 설정

표준 방법을 사용하여 최선의 전술을 반복적으로 생성하고 형식적 증명 내에서 중간 증명 단계를 검증하는 방식으로 평가를 수행했습니다. 각 생성 단계에서는 최대 \(K\) 확장이 허용되는 단일 반복에서 상태 \(S_i\)를 확장하여 \(S\) 전술 후보를 생성했습니다. \(S = 32\) 및 \(K = 100\)으로 설정되었습니다.

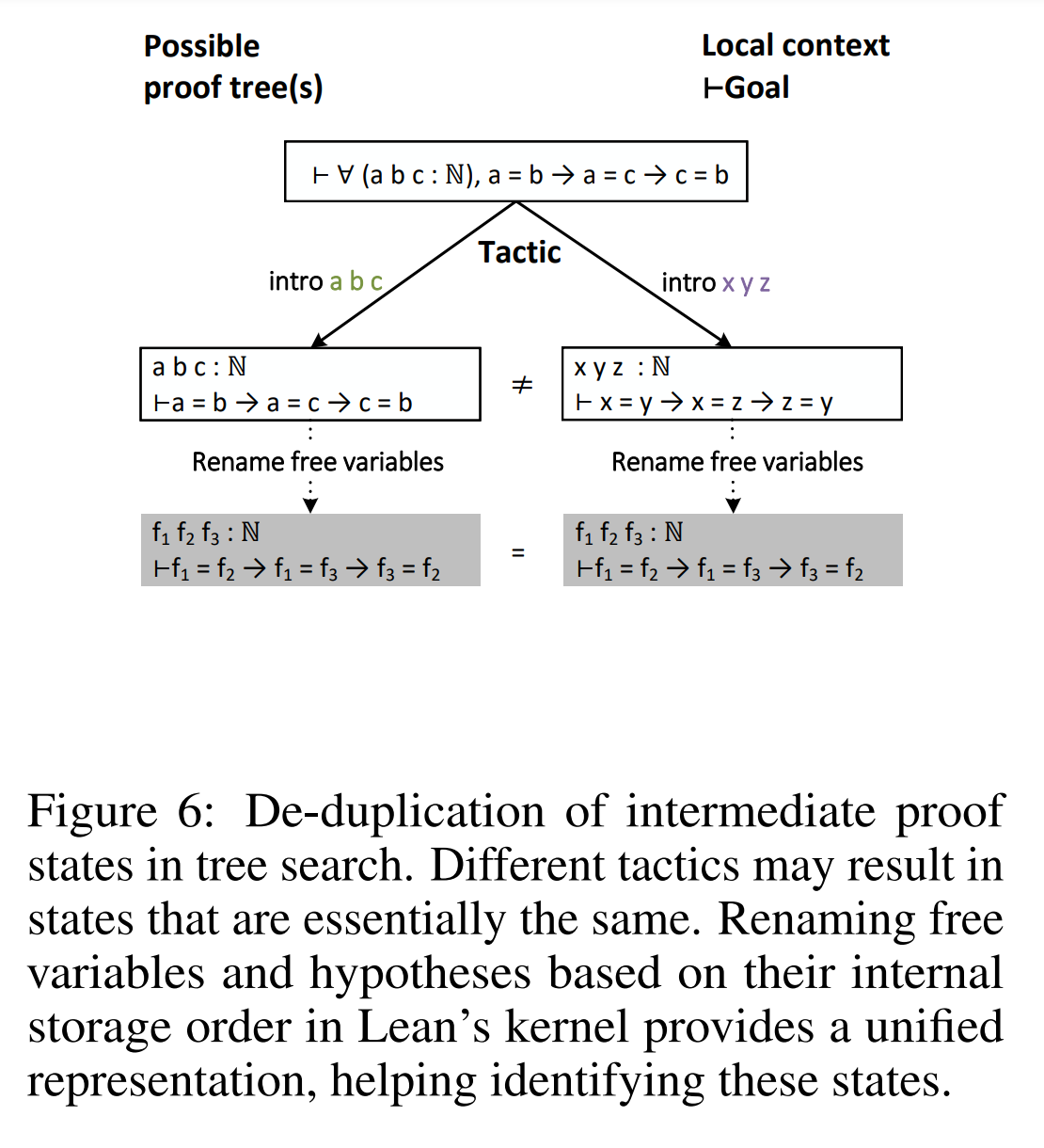
상태 중복 제거는 Lean의 기본적인 타입 이론에 뿌리를 둔 Lean 언어의 본질적인 특성으로 인해 발생하는 가장 일반적인 문제 중 하나입니다. Lean에서 모든 명제는 유효한 타입으로 간주되며, 해당 명제를 입증하는 것은 그 타입의 요소를 발견하거나 구성하는 것과 유사합니다. 따라서 Lean은 두 명제의 증명을 정의적으로 동일하다고 간주합니다. 이로 인해 동일한 중간 상태로 이어지는 두 증명을 구별하는 본질적인 메커니즘이 없습니다. 중복 상태 문제를 해결하기 위해 Lean의 메타 프로그래밍 기능을 활용하여 중복 제거에 필요한 추가 정보를 제공하였습니다.

(사견) 비단 수학적 정리 문제를 제외하고 다른 도메인도 비슷할 것

4.2 주요 결과

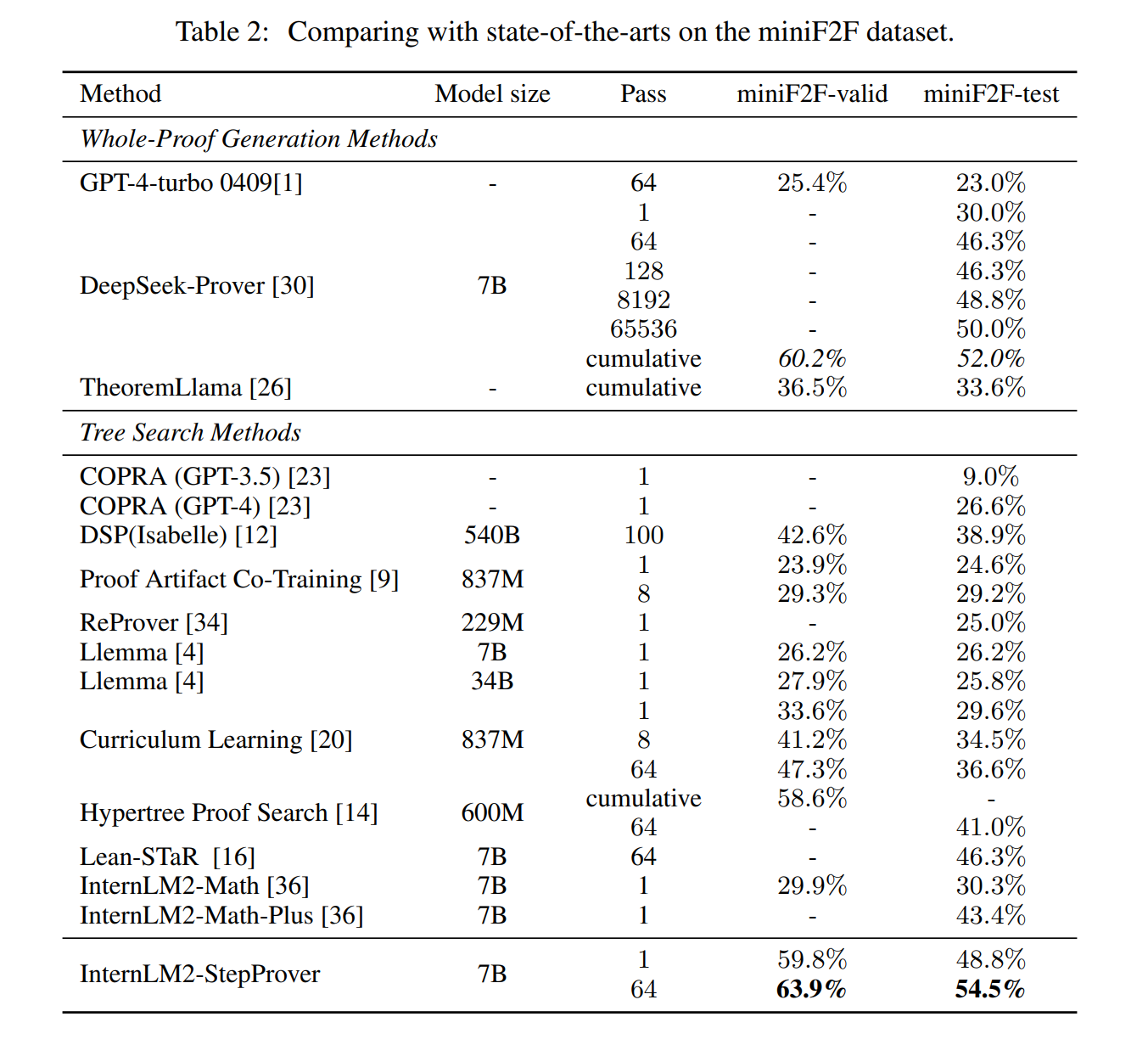
다양한 수준(고등학교 또는 대학 수준), 난이도(일반 연습 문제 또는 올림피아드 문제), 그리고 문제 해결과 수학 체계 구축 사이의 차이점을 목표로 하는 Lean 4 벤치마크를 사용하여 테스트한 결과, InternLM2-StepProver는 기존 작업보다 향상된 형식적 인퍼런스 능력을 보여주었습니다.

miniF2F 결과에서는 miniF2F 검증 및 테스트 데이터셋에서 각각 63.9% 및 54.5%의 누적 정확도를 달성하여, DeepSeek-Prover [30]를 포함한 모든 Baseline Model을 상회했습니다. ProofNet [3]에서는 학부 수준의 수학에 대한 형식적 인퍼런스 능력을 테스트하며, 18.1%의 Pass@1 비율로 기존 리더인 ReProver [34]를 능가했습니다. PutnamBench [25]에서는 640개 문제 중 5개를 단일 패스로 해결하여 현재까지 ITP에서 해결된 것으로 보고되지 않은 Putnam 1988 B2 문제에 대한 해결책을 제시했습니다.

4.3 소거 연구

• 데이터 출처 제거(ablation) 연구는 LEAN-GitHub 데이터셋의 효과를 입증하며, 여러 데이터 조합에서 가장 효과적임을 보여줌.
• 여러 인퍼런스를 통해 성능이 향상됨을 관찰하며, LEAN-GitHub이 최대 성능에 긍정적 영향을 미침을 시사.
• 테스트 결과는 LEAN-GitHub 데이터를 사용한 모델이 다양한 형식 인퍼런스 작업에서 성능을 개선함을 보여줌.

데이터 소스 소거

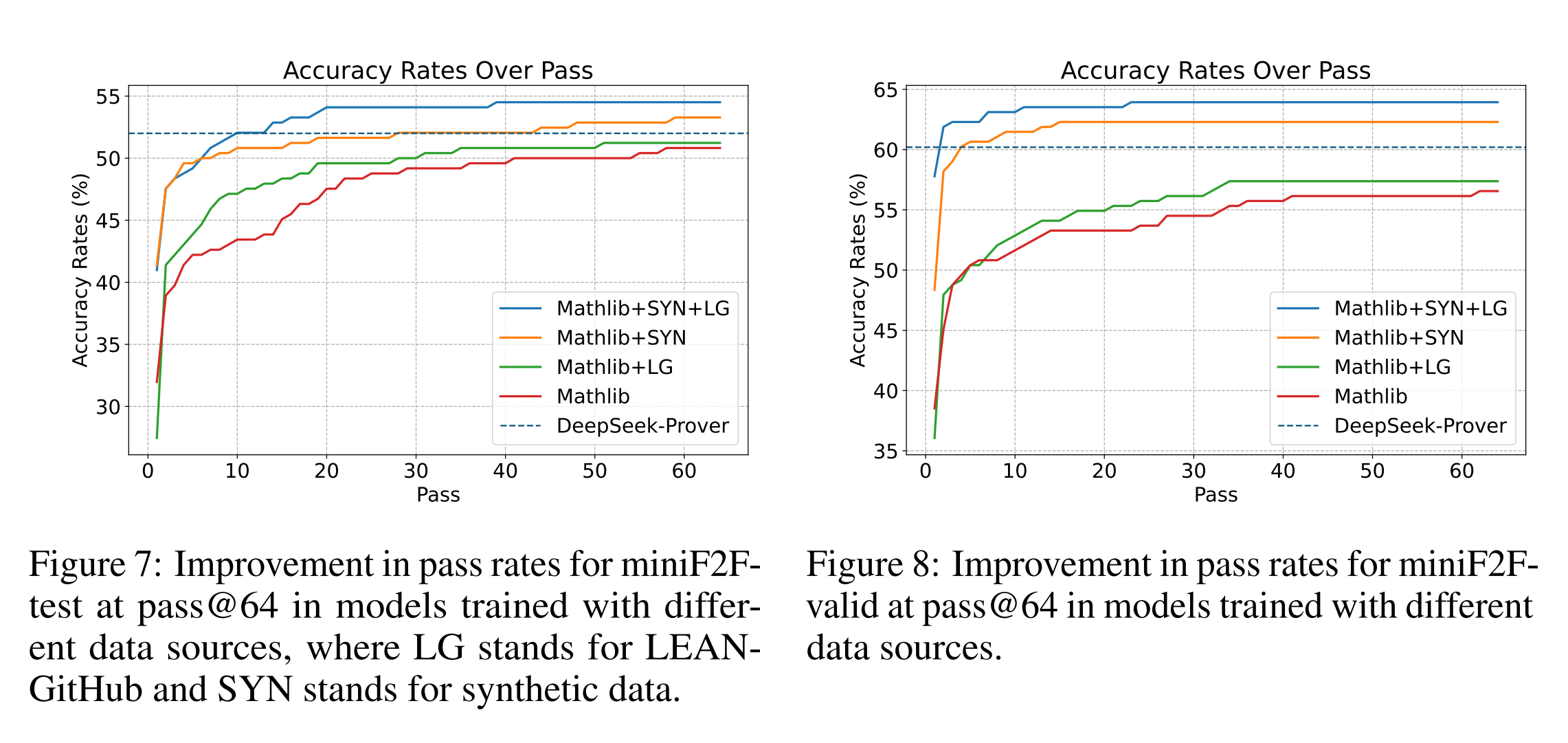
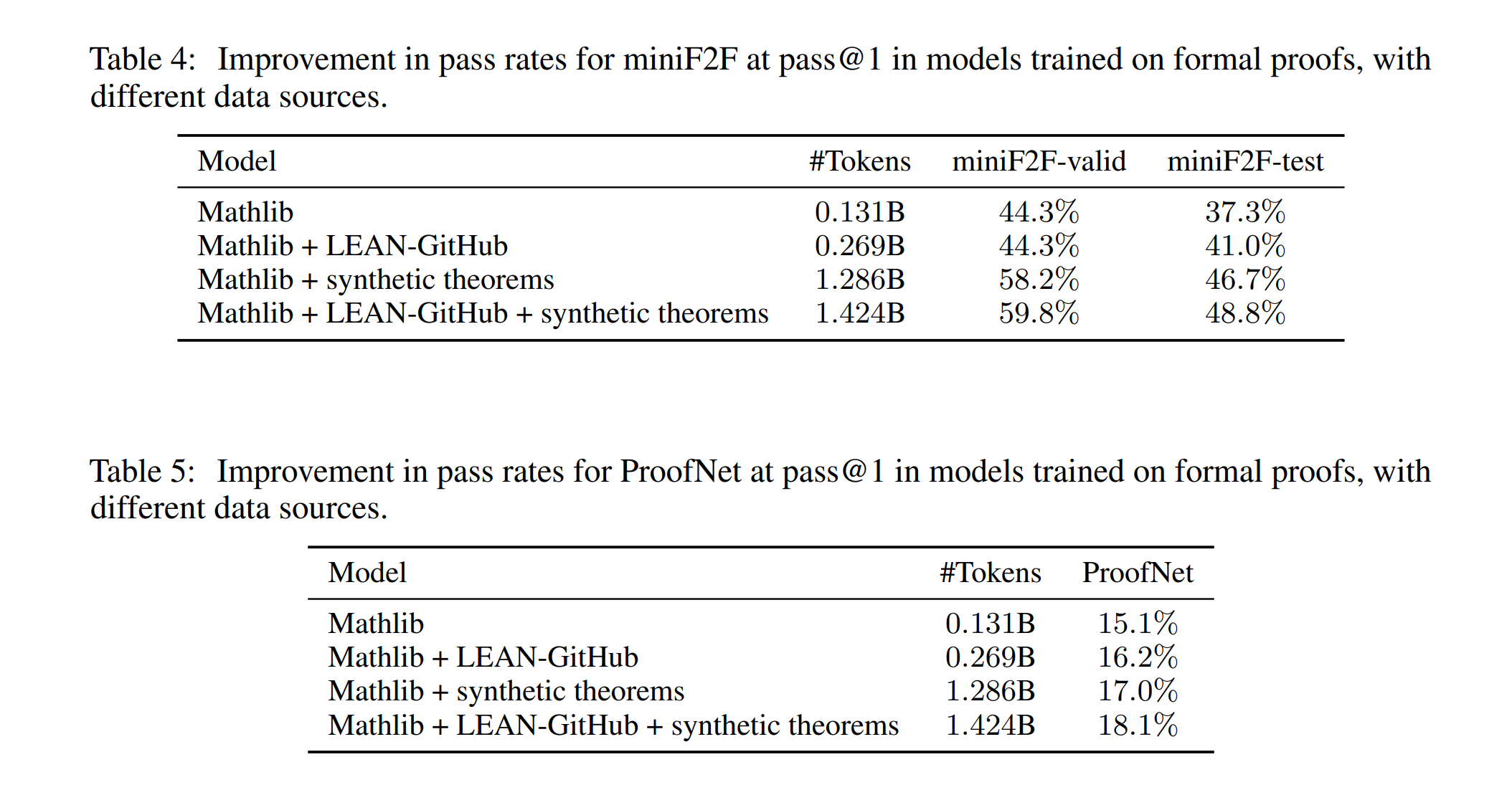
InternLM2-StepProver는 LEAN-GitHub, 합성 데이터(규칙 기반 생성된 방정식과 부등식 포함), 그리고 Mathlib에서 추출된 휴먼 작성 데이터를 포함하여 훈련되었습니다. LEAN-GitHub 데이터셋의 효과를 입증하기 위해, 다양한 훈련 데이터 조합의 비교 분석을 수행하였습니다. 결과에 따르면, GitHub에서 추출된 데이터를 포함하여 훈련된 모델이 Mathlib 데이터만을 사용하여 훈련된 모델이나 합성 데이터를 사용한 모델들보다 월등히 향상된 성능을 보였습니다.

다중 인퍼런스의 효과성

또한, 평가를 확장할 때(즉, 더 많은 패스 시간을 허용할 때) LEAN-GitHub이 형식적 인퍼런스 성능에 어떤 영향을 미치는지 집중적으로 분석했습니다. 형식화 시스템이 문제가 해결되었는지 알려주기 때문에 최대 성능을 추구하는 경우 모델을 단일 패스로 제한할 이유가 없습니다. 성능 향상이 미미해질 때까지 평가 예산을 확장함으로써 관찰된 결과는 LEAN-GitHub이 모델의 최대 성능을 향상시키는 데 도움이 된다는 것을 보여줍니다.

평가는 0.7과 1.0의 온도에서 각각 32개의 독립적인 인퍼런스를 사용하여 수행되었으며, Pass@1 평가에 사용된 빔 검색 대신 선택되었습니다. 따라서 첫 번째 라운드의 초기 정확도는 Pass@1 평가보다 낮을 수 있습니다. InternLM2-StepProver는 miniF2F-test에서 54.5%의 누적 패스율과 miniF2F-valid에서 63.9%를 달성하여, LEAN-GitHub 없이 훈련된 Baseline Model의 패스율 53.2%와 62.3%를 상회했습니다. Mathlib만을 사용하여 훈련된 모델과 Mathlib+LEAN-GitHub을 사용하여 훈련된 모델에서도 동일한 경향이 관찰되었습니다.

5 Conclusion

이 논문에서는 GitHub의 오픈 Lean 4 저장소에서 추출된 대규모 공식 데이터를 포함하는 LEAN-GitHub 데이터셋을 소개합니다. 이 데이터셋을 사용하여 훈련된 InternLM2-StepProver는 Lean 4 형식 인퍼런스에서 상위 모델 성능을 보여줍니다. 또한, 다양한 모델을 LEAN-GitHub와 함께 훈련하여 데이터셋에서 달성할 수 있는 형식적 인퍼런스 성능을 평가했습니다. 특히, LEAN-GitHub에서 훈련된 모델은 다양한 분야와 난이도 수준에서 형식 인퍼런스 성능을 향상시키는 것으로 나타났으며, 잘 추출된 다양한 데이터셋이 다양한 인퍼런스 작업에서 모델 성능을 향상시킬 수 있음을 보여줍니다. LEAN-GitHub를 공개함으로써, 커뮤니티가 원시 코퍼스에서 활용되지 않은 정보를 더 잘 활용하고 수학적 인퍼런스 능력을 개선하는 데 도움을 줄 수 있기를 기대합니다.

https://github.com/dwrensha/compfiles/blob/main/Compfiles/Imo1983P6.lean

Appendix A. Case Study

Case 1: 이항 계수

[자연어 문제] 양의 정수 \(n\)과 \(k\)에 대해 \(k \leq n\)이면, 다음이 성립함을 보여라.

이 경우 InternLM2-StepProver는 간단한 귀납법을 사용할 수 있음을 보여줍니다. 또한, 이는 고등학교 수준의 수론 문제와 대수 문제를 해결할 수 있습니다.

Case 2: 퍼트넘 1988 B2

[자연어 문제] 실수 \(x\)와 \(y\)가 \(y \geq 0\)이고 \(y(y + 1) \leq (x + 1)^2\)를 만족할 때, \(y(y - 1) \leq x^2\)임을 증명하거나 반증하라.

이 증명에서는 먼저 연결을 두 가지 함의로 분할하고, 각각을 하위 목표로 설정합니다. 후자의 목표는 자동으로 닫히며 간단합니다. InternLM2-StepProver는 자동 전술인 ring_nf와 nlinarith를 사용하여 다른 하위 목표를 닫습니다. 증명의 핵심 단계는 적절한 힌트(e.g., sq_nonneq)를 자동 전술에 제공하는 것입니다.

Case 3: IMO 1964 P1(2)

[자연어 문제] 7로 나누어지는 양의 정수 \(n\)이 존재하지 않음을 증명하라.

IMO 1964 P1은 상대적으로 간단한 첫 번째 부분과 더 복잡한 두 번째 부분으로 구성된 복합 문제입니다. 공식화된 버전에서는 첫 번째 부분의 보조 정리를 생략하여 문제의 난이도를 실제로 높였습니다. 문제를 해결하는 핵심은 \(2^n \mod 7\)의 주기를 찾는 것이며, 증명자는 이 주기가 3임을 확인하고 이를 바탕으로 Case 분석을 수행하여 문제를 성공적으로 해결했습니다.

Case 4: Pough 3.2.8

[자연어 문제] \(G\)의 유한 부분군 \(H\)와 \(K\)의 차수가 서로소일 때 \(H \cap K = 1\)임을 증명하라.

InternLM2-StepProver는 또한 대학 수준의 문제를 해결할 수 있는 능력을 보여줍니다. 이 경우, 군과 서로소에 대한 지식을 활용해야 합니다. 이 Case는 LEAN-GitHub이 다양한 수학적 인퍼런스 작업에서의 효과를 보여줍니다.