QA LoRA***
- Related Project: Private
- Category: Paper Review
- Date: 2023-09-29
QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models
- url: https://arxiv.org/abs/2309.14717
- pdf: https://arxiv.org/pdf/2309.14717
- abstract: Recently years have witnessed a rapid development of large language models (LLMs). Despite the strong ability in many language-understanding tasks, the heavy computational burden largely restricts the application of LLMs especially when one needs to deploy them onto edge devices. In this paper, we propose a quantization-aware low-rank adaptation (QA-LoRA) algorithm. The motivation lies in the imbalanced degrees of freedom of quantization and adaptation, and the solution is to use group-wise operators which increase the degree of freedom of quantization meanwhile decreasing that of adaptation. QA-LoRA is easily implemented with a few lines of code, and it equips the original LoRA with two-fold abilities: (i) during fine-tuning, the LLM’s weights are quantized (e.g., into INT4) to reduce time and memory usage; (ii) after fine-tuning, the LLM and auxiliary weights are naturally integrated into a quantized model without loss of accuracy. We apply QA-LoRA to the LLaMA and LLaMA2 model families and validate its effectiveness in different fine-tuning datasets and downstream scenarios. Code will be made available at this https URL.
Contents
- QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models
TL;DR
- 양자화와 저차원 적응 결합: 본 논문에서는 언어 모델의 양자화 및 저차원 적응을 결합한 새로운 방법, Quantization-Aware Low-Rank Adaptation (QA-LoRA)를 제안한다.
- 효율적 fine-tuning 및 배치: QA-LoRA는 기존 모델에 비해 메모리와 계산 비용을 절감하면서도 정확도 손실 없이 fine-tuning과 배치가 가능하다.
- 다양한 데이터셋 및 모델 크기에 대한 검증: LLaMA와 LLaMA2 모델 가족을 사용하여 여러 언어 이해 벤치마크에서 QA-LoRA의 효과를 확인하였다.
1 서론
최근 대규모 언어모델(LLMs)은 다양한 언어 이해 작업에서 향상된 성능을 보여 주고 있다. 이런 모델들은 많은 파라미터를 가지고 있어 계산 부담이 크기 때문에, 이를 효과적으로 조정하고 배치하는 것이 중요한 연구 주제이다. 특히, 양자화와 저차원 적응이 이 문제를 해결하는 두 가지 주요 접근 방식이다.
1.1 양자화
양자화는 모델의 파라미터나 활성화를 저비트로 변환하여 저장 공간과 계산 비용을 줄이는 기술이다. 그러나 이런 접근 방식은 종종 낮은 비트 폭에서 정확도가 떨어지는 문제를 보고한다.
1.2 저차원 적응
저차원 적응(LoRA)는 높은 차원의 원래 가중치에 저차원의 행렬을 추가하여 fine-tuning하는 방식이다. 이 방법은 전체 파라미터를 조정하는 것보다 훨씬 적은 파라미터로 유사한 성능을 달성할 수 있다.
2 관련 연구
양자화와 저차원 적응을 통합한 연구는 여전히 초기 단계에 있으며, 이 두 기술을 효과적으로 결합하는 것은 큰 챌린지이다. 본 논문은 이 두 기술의 통합을 통해 계산 효율성과 배치 용이성을 동시에 달성하고자 한다.
3 제안하는 접근 방식
3.1 기초: 저차원 적응 및 양자화
LoRA 기법은 기존의 가중치에 저차원 행렬을 추가하여 언어 모델을 fine-tuning하는 기술이다. 본 논문에서 제안하는 QA-LoRA는 LoRA의 저차원 가중치와 양자화된 모델 가중치를 통합하여 새로운 방식으로 fine-tuning을 수행한다.
3.2 목표: 효율적인 적응 및 배치
QA-LoRA의 목표는 fine-tuning 단계에서 저비트 표현을 사용하여 계산 효율을 극대화하고, 배치 단계에서는 fine-tuning된 저비트 가중치를 그대로 사용하여 계산 비용을 줄이는 것이다.
3.3 솔루션: 그룹별 양자화와 저차원 적응
그룹별 양자화와 저차원 적응을 통해 각 그룹별로 적응 파라미터를 공유하고, 각 그룹에 대해 개별적으로 양자화를 수행하여 전체 모델의 효율성을 높인다.
4 실험
4.1 실험 설정
LLaMA와 LLaMA2 모델을 사용하여 다양한 크기의 모델에서 MMLU 벤치마크와 상식적 질문 답변 작업을 평가한다.
4.2 주요 결과 및 효율성
QA-LoRA는 QLoRA 및 기타 양자화 기법과 비교하여 높은 정확도와 더 낮은 계산 비용을 보여준다. 또한, QA-LoRA는 낮은 비트 폭에서도 높은 성능을 유지한다.
5 결론
QA-LoRA는 저차원 적응과 양자화를 효과적으로 결합하여 LLMs의 효율적인 fine-tuning과 배치를 가능하게 한다. 이 방법은 다양한 언어 이해 작업에서 향상된 성능을 보여 주며, 계산 비용을 크게 절감한다.
[참고자료 1] QA-LoRA 상세
3.2 목표: 효율적인 적응 및 배포
LoRA(Hu et al., 2021)에서 사용된 기호 체계를 따르며, 사전 학습된 가중치가 매트릭스 $W$를 형성하고 피처는 벡터 $x$를 형성한다고 가정합니다. 이 정의는 다양한 시나리오에 쉽게 적용될 수 있으며 $x$가 벡터 집합(e.g., 피처 매트릭스)이 될 수 있도록 확장됩니다. $W$의 크기를 $D_{in} \times D_{out}$으로, $x$의 길이를 $D_{in}$으로 두면, 계산은 쉽게 $y = W^\top x$로 작성될 수 있으며, $y$는 길이가 $D_{out}$인 출력 벡터입니다.
핵심 아이디어
LoRA의 핵심 아이디어는 $W$를 보완하기 위해 두 개의 매트릭스 $A$와 $B$를 도입하는 것입니다. $A$와 $B$의 크기는 각각 $D_{in} \times D_{int}$와 $D_{int} \times D_{out}$이며, 그 곱 $AB$는 $W$와 동일한 크기를 갖습니다. 중간 차원 $D_{int}$는 가끔 작은 값으로 설정되며($D_{int} \ll \min{D_{in}, D_{out}}$), $AB$를 $W$에 비해 저차원 매트릭스로 만듭니다. 파인튜닝 중에는 $y = W^\top x + s \cdot (AB)^\top x$로 계산되며, $s$는 가중치 튜닝 계수이고 $W$는 고정된 상태로 $A$와 $B$는 조정될 수 있습니다. 파인튜닝 후, 계산은 $y = (W + s \cdot AB)^\top x$로 재구성되며, $W$는 빠른 인퍼런스를 위해 $W’ = W + s \cdot AB$로 대체됩니다.
양자화 기법
계산 비용을 줄이는 또 다른 효과적인 방법은 저비트 양자화입니다. 이 논문에서는 가중치의 양자화만을 고려합니다. 특히, min-max 양자화라는 간단한 방법을 적용합니다. 수학적으로, 비트 폭 $N$과 사전 학습된 가중치 매트릭스 $W$가 주어지면, $W$의 모든 요소에 대한 최소값과 최대값을 각각 $\min(W)$와 $\max(W)$로 계산합니다. 그런 다음 $W$는 다음과 같이 양자화됩니다.
\[\tilde{W}_{i,j} = \left\lfloor \frac{W_{i,j} - \beta}{\alpha} \right\rceil\]$\alpha = \frac{\max(W) - \min(W)}{2^N - 1}$이고, $\beta = \min(W)$는 각각 스케일링 및 영점 요소이며, $\lfloor \cdot \rceil$는 정수 반올림 연산을 나타냅니다. $\tilde{W}$의 모든 요소는 ${0, 1, \ldots, 2^N - 1}$ 집합에 속하며 $B$ 비트 정수로 저장됩니다. 계산, $y = W^\top x$는 $y = \tilde{W}^\top x = \alpha \cdot \hat{W}^\top x + \beta x$로 근사화됩니다. 양자화는 $W$의 저장 공간을 줄이고(e.g., FP16에서 INT4로) $W^\top x$의 계산을 더 빠르게 만듭니다.
양자화 손실 감소
$\tilde{W}$가 $W$의 근사값이므로, 이는 언어 이해의 정확도를 해칠 수 있습니다. $W$와 $\tilde{W}$ 사이의 양자화 손실을 줄이기 위한 효과적인 전략은 $W$의 각 열에 대해 개별 양자화를 수행하는 것입니다. \(W = [w_{i,j}]_{D_{in} \times D_{out}}\)로 두고, \(i \in \{1, \ldots, D_{in}\}\) 및 \(j \in \{1, \ldots, D_{out}\}\)은 반복 변수입니다. \(w_j\)의 \(j\)-번째 열에 대해 계산된 스케일링 및 영점 요소를 \(\alpha_j\) 및 \(\beta_j\)로 둡니다. 따라서 식은 다음과 같이 업데이트됩니다.
\[\tilde{W} = [\tilde{w}_j]_{D_{out}}.\]기존의 (전체적인) 양자화에서는 계산 비용은 변하지 않지만 스케일링 및 영점 요소의 저장 비용은 $2$에서 $2D_{out}$ 부동 소수점 숫자로 증가합니다. 이는 전체 Precision의 $W$를 저장하는 비용에 비해 무시할 수 있습니다.
3.2 목표: 효율적인 적응 및 배포
두 가지 목표를 달성하고자 합니다. 첫째, 파인튜닝 단계에서 사전 학습된 가중치 $W$를 저비트 표현으로 양자화하여 LLM이 가능한 한 적은 GPU에서 파인튜닝될 수 있도록 하는 것입니다. 둘째, 파인튜닝 단계 후에도 파인튜닝 및 병합된 가중치 $W’$가 여전히 양자화된 형태로 유지되어 LLM이 계산 효율성을 가지고 배포될 수 있도록 하는 것입니다.
QLoRA (Dettmers et al., 2023a)는 최근 제안된 LoRA의 변형으로, 첫 번째 목표를 달성했습니다. 아이디어는 파인튜닝 단계에서 $W$를 FP16에서 NF4(매우 압축된 유형의 부동 소수점 숫자)로 양자화하는 것입니다. QLoRA에서 양자화와 적응의 공동 최적화가 가능함을 배웠습니다. 왜냐하면 $W$와 $\tilde{W}$ 사이의 정확도 손실이 저차원 가중치 $s \cdot AB$로 보상되기 때문입니다. 파인튜닝 후, 측면 가중치 $s \cdot AB$는 $\tilde{W}$에 다시 추가되어 최종 가중치 $W’$가 다시 FP16이 됩니다. 실제로 $W’$에 대해 후속 훈련 양자화(PTQ)를 수행할 수 있지만, 이 전략은 특히 비트 폭이 낮을 때 정확도에 큰 손실을 초래할 수 있습니다. 실험을 참조하십시오. 또한, 아직 NF4에 대한 연산자 수준 최적화가 없어, 파인튜닝 및 인퍼런스 단계를 가속화하기 어렵습니다. 간단히 말해, QLoRA가 가져오는 유일한 이점은 파인튜닝을 위한 메모리 비용이 감소한다는 것입니다.
3.3 해결책: 저차원 적응과 그룹 단위 양자화
위의 분석에서, 두 번째 목표를 달성하기 위한 핵심은 $\tilde{W}$ (즉, 양자화된 $W$)와 $s \cdot AB$를 고정밀 숫자(FP16 등)를 사용하지 않고 병합하는 것입니다. 이것이 원래 설정에서는 불가능함을 먼저 언급합니다. 즉, $W$는 열 단위로 $\tilde{W}$로 양자화되는 반면, $A$와 $B$는 제약을 받지 않습니다.
조건을 수학적으로 작성하면, \(W' = \tilde{W} + s \cdot AB\)이므로, 모든 \((i, j)\)에 대해 \(w'_{i,j} = \tilde{w}_{i,j} + s \cdot \sum_k a_{i,k}b_{k,j}\)을 갖습니다. \(j\)에 대해 모든 \(\tilde{w}_{i,j}\)는 동일한 스케일링 및 영점 요소 집합을 사용하여 표현됩니다. 즉, \(\tilde{w}_{i,j} = \alpha_j \times \hat{w}_{i,j} + \beta_j\), \(\hat{w}_{i,j} \in \{0, 1, \ldots, 2^N - 1\}\)이 되도록 하는 \(\alpha_j\)와 \(\beta_j\)가 존재합니다. 각 \(\tilde{w}_{i,j}\)에 \(s \cdot \sum_k a_{i,k}b_{k,j}\) (약칭 \(c_{i,j}\))을 추가하면, 양자화 속성을 유지하려면 \(j\)에 대해 모든 가능한 \(c_{i,j}\) 값이 동일한 공차를 가진 산술 집합을 형성해야 합니다. 이는 연속적이고 기울기 기반 최적화에서 실현 불가능합니다. 따라서 모든 \(a_{i,k}\)가 동일한 값을 갖도록 설정해야 합니다. 즉, \(a_1 \equiv \ldots \equiv a_i \equiv \ldots \equiv a_{D_{in}}\), \(\equiv\)는 두 벡터 간의 요소별 동등성을 나타냅니다.
위 전략은 실현은 가능하지만, 실제로는 상당한 정확도 저하를 초래합니다. 특히, $A$의 모든 행이 동일한 벡터가 되면, $\text{rank}(A) = 1$이 되고, 따라서 $\text{rank}(AB) = 1$이 됩니다.
그러나 $AB$의 순위는 새로운 데이터에서 $\tilde{W}$를 파인튜닝하는 능력과 관련이 있다고 알려져있으므로(Hu et al., 2021; Valipour et al., 2022; Dettmers et al., 2023a), 이를 해결하기 위해 제약 조건을 완화하는 다음과 같은 간단한 아이디어가 제안되었습니다.
$W$의 각 열을 $L$ 그룹으로 분할합니다. 구현의 용이성을 위해 $L$을 $D_{in}$의 약수로 설정하고, $W$의 각 열을 완전히 양자화하는 대신 각 그룹의 요소 수 $D_{in}/L$에 대해 별도의 스케일링 및 영점 요소 쌍, 즉 $\alpha_{l,j}$와 $\beta_{l,j}$를 사용합니다.
따라서, 같은 그룹 내 $A$의 행 벡터만 동일한 값을 갖도록 하며, 이는 입력 벡터 $x$의 각 그룹 내 합계를 통해 구현됩니다.
이 파라미터 없는 연산은 $x$의 차원을 $D_{in}$에서 $L$로 줄이므로 추가적인 제약 없이 $A$를 $L \times D_{int}$ 매트릭스로 설정할 수 있습니다.
QA-LoRA
제안된 접근 방식은 양자화 인식 저차원 적응(QA-LoRA)이라고 합니다. 기본 모델 LoRA 및 QLoRA와 비교하여, QA-LoRA는 몇 줄의 코드 삽입/수정으로 구현됩니다. LoRA와 비교할 때, QA-LoRA는 시간과 메모리 소비에서 이점을 누립니다. QLoRA와 비교할 때, QA-LoRA는 $L \times D_{out}$ 쌍의 스케일링 및 영점 요소를 추가로 저장해야 하지만, $A$의 파라미터 수는 $D_{in} \times D_{int}$에서 $L \times D_{int}$로 줄어듭니다. $L \ll D_{in}$로 설정하는 경우, 이런 변화는 무시할 수 있습니다. QA-LoRA의 주요 이점은 인퍼런스 단계에서 더 빠르고 정확하다는 것입니다. Table 2에서 LoRA, QLoRA 및 QA-LoRA의 계산 비용을 비교합니다.
QA-LoRA의 통찰력: 균형
QA-LoRA는 NF4 양자화가 INT4로 대체된 QLoRA의 변형과 유사합니다. 이 버전에서는 양자화 파라미터($D_{out}$ 쌍의 스케일링 및 영점 요소) 수가 적응 파라미터($D_{in} \times D_{int} + D_{int} \times D_{out}$) 수에 비해 훨씬 적습니다. 이는 양자화와 적응의 자유도 간의 큰 불균형을 초래합니다. 그룹 단위 연산을 도입하여 양자화 파라미터의 수를 $D_{out}$에서 $L \times D_{out}$로 증가시키는 한편, 적응 파라미터의 수를 $D_{in} \times D_{int} + D_{int} \times D_{out}$에서 $L \times D_{int} + D_{int} \times D_{out}$로 감소시킵니다. 실험에서 보듯이, 적절한 $L$은 계산 효율성을 유지하면서 언어 이해에서 더 나은 정확도를 달성할 수 있습니다.
1 INTRODUCTION
Recently, large language models (LLMs) (Brown et al., 2020; Scao et al., 2022; Zhang et al., 2022; Touvron et al., 2023a; Chowdhery et al., 2022; OpenAI, 2023; Zeng et al., 2023) have shown unprecedented performance across a wide range of language understanding tasks (Wei et al., 2022a) and served as the foundation of state-of-the-art chat systems (Bubeck et al., 2023). The diversity of real-world applications calls for a pipeline in which LLMs can be fine-tuned to fit different scenarios and quantized to be deployed onto edge devices (e.g., mobile phones), and the key issue is to get rid of the heavy computational burden brought by the large number of parameters of LLMs.
There are two lines of research for this purpose. The first one is parameter-efficient fine-tuning (PEFT) (Houlsby et al., 2019; Li & Liang, 2021; Liu et al., 2021; He et al., 2022; Hu et al., 2021) which introduced a small number of learnable parameters while keeping most pre-trained parameters unchanged. Among them, low-rank adaptation (LoRA) (Hu et al., 2021), a popular PEFT algorithm, proposed to fine-tune low-rank matrices to complement the pre-trained weights. Despite the comparable performance to full-parameter fine-tuning, the memory usage of LoRA is still large, especially when the base LLM is large (e.g., LLaMA-65B). The second one studies parameter quantization (Yao et al., 2022; Dettmers et al., 2022; Wei et al., 2022b; Frantar et al., 2023; Lin et al., 2023; Xiao et al., 2023; Dettmers et al., 2023b) where the trained weights are quantized into low-bit integers or floating point numbers. Although these methods can alleviate the computational burden, they often report unsatisfying accuracy especially when the quantization bit width is low.
Hence, it is an important topic to integrate PEFT with quantization. A naive solution is to perform post-training quantization (PTQ) after PEFT, but it reports unsatisfying accuracy especially when the quantization bit width is low. Advanced methods exist, but they are either computationally expensive in the fine-tuning stage (Liu et al., 2023) or unable to maintain the quantized property after fine-tuning (Dettmers et al., 2023a). In this paper, we propose a simple yet effective method for quantization-aware low-rank adaptation (QA-LoRA). Our idea is based on the imbalanced degrees of freedom for quantization and adaptation. Specifically, each column of the pre-trained weight matrix is accompanied by only one pair of scaling and zero parameters but many more LoRA parameters. This imbalance not only results in large quantization errors (which harm the LLM’s accuracy), but also makes it difficult to integrate the auxiliary weights into the main model. QA-LoRA addresses the issue by introducing group-wise operators which increase the degree of freedom of low-bit quantization (each group is quantized individually) and decrease that of LoRA (each group shares the adaptation parameters). QA-LoRA enjoys two-fold benefits: (i) an efficient fine-tuning stage thanks to the LLM’s weights being quantized into low-bit integers; (ii) a lightweight, finetuned model without the need for PTQ which often incurs loss of accuracy.
Figure 1: The comparison of 5-shot MMLU accuracy (%) with different quantization bit widths based on the LLaMA model family. QLoRA (NF4 & FP16) refers to the original QLoRA models with pre-trained weights in INT4 and adapter weights in FP16, and QLoRA (INT4) refers to performing post-training quantization (into INT4) upon the merged QLoRA models. All models are fine-tuned on the Alpaca dataset. Full results are provided in Table 1.
QA-LoRA is easily implemented and applies to a wide range of scenarios. We evaluate QA-LoRA on the LLaMA and LLAMA2 model families (Touvron et al., 2023a;b) and validate it on various language understanding benchmarks. Figure 1 compares the 5-shot accuracy on the MMLU benchmark of QA-LoRA and the direct baseline, QLoRA (Dettmers et al., 2023a) with and without PTQ, when both methods are fine-tuned on the Alpaca dataset. QA-LoRA consistently outperforms QLoRA with PTQ on top of LLMs of different scales (the advantage becomes more significant when the quantization bit width is lower) and is on par with QLoRA without PTQ. Note that during inference, QA-LoRA has exactly the same complexity as QLoRA with PTQ and is much more efficient than QLoRA without PTQ. Hence, QA-LoRA serves as an effective and off-the-shelf method for joint quantization and adaptation of LLMs.
2 RELATED WORK
Large language models (LLMs) (Devlin et al., 2019; Brown et al., 2020; Zhao et al., 2023a; Hadi et al., 2023) have emerged as a dominant paradigm in natural language processing which has achieved state-of-the-art performance on various tasks (Zhao et al., 2023b; Zhou et al., 2023) and served as the fundamental of chat systems (OpenAI, 2023). However, their deployment in real-world scenarios is hindered by their high computational and memory requirements during inference (Chang et al., 2023). To tackle this issue, various methods have been proposed, including distillation (Liu et al., 2023), quantization (Yao et al., 2022; Dettmers et al., 2022; Wei et al., 2022b; Frantar et al., 2023; Lin et al., 2023; Xiao et al., 2023), pruning (Frantar & Alistarh, 2023; Ma et al., 2023; Sun et al., 2023), etc. (Weng, 2023). This paper mainly focuses on the quantization of LLMs.
Fine-tuning LLMs with adapters. Parameter efficient fine-tuning (PEFT) is an important topic for LLMs. One of the most popular approaches is low-rank adaptation (LoRA) (Hu et al., 2021; Valipour et al., 2022), where the key insight is to decompose the adapter weights into the multiplication of two low-rank (and thus parameter-efficient) matrices. LoRA has claimed comparable performance to full fine-tuning while using much fewer learnable parameters. Meanwhile, there are also other branches of adapters for LLMs such as the series adapter (Houlsby et al., 2019) and parallel adapter (He et al., 2022). Please refer to (Mangrulkar et al., 2022; Hu et al., 2023) for a review of these adapters.
Quantization of LLMs. Quantization is a compression technique that reduces the bit width of the parameters and/or activations of LLMs to improve their efficiency and scalability (Xiao et al., 2023; Dettmers et al., 2022; 2023a). Existing methods mostly focused on preserving or restoring the accuracy of quantized LLMs during the inference stage (Zhu et al., 2023), where the key is to reduce the memory footprint and computational costs without re-training the LLMs. One of the main challenges is to handle the outliers in the parameter distribution (Xiao et al., 2023), which can cause significant errors when quantized. To address this issue, some methods proposed to use either adaptive or dynamic quantization schemes that adjust the quantization range or precision according to the parameters (Xiao et al., 2023; Dettmers et al., 2022). Other methods used sophisticated grouping or clustering techniques to partition the parameters into different groups and applied different quantization strategies for each group (Park et al., 2022; Yao et al., 2022; Wu et al., 2023).
Joint adaptation and quantization. This paper aims to achieve the objectives of both parameterefficient adaptation and computation-efficient tuning and deployment, which can further improve the efficiency and scalability of LLMs as well as mitigate the negative impact of quantization errors. However, this also poses additional challenges, such as propagating gradients through discrete values and optimizing the quantization parameters. To overcome these challenges, lossy quantization methods proposed to use stochastic rounding (Shen et al., 2020) or learned rounding (Esser et al., 2019) to approximate the gradients and update the parameters, but applying these methods to LLMs is often difficult. Other methods proposed to use switchback layers (Wortsman et al., 2023) or mixed-precision inference (Dettmers et al., 2023a) to alternate between quantized and full/halfprecision values, which often result in low inference speed.
To the best of our knowledge, the most related work is QLoRA (Dettmers et al., 2023a) which squeezed the pre-trained weights into NF4 and added LoRA. However, QLoRA added the adaption weights back to pre-trained weights and turned them into FP16 again, and thus the deployed model is still slow. We solve this problem with the proposed QA-LoRA approach.
3 THE PROPOSED APPROACH
3.1 BASELINE: LOW-RANK ADAPTATION AND LOW-BIT QUANTIZATION
We follow the notation system used in LoRA (Hu et al., 2021) which assumed pre-trained weights to form a matrix $W$ and the features form a vector $x$. The definition is easily applied to a wide range of scenarios and extended into $x$ is a set of vectors (e.g., a feature matrix). Let the size of $W$ be $D_{in} \times D_{out}$ and $x$ has the length of $D_{in}$, and thus the computation is easily written as $y = W^\top x$ where $y$ is the output vector with a length of $D_{out}$.
The key idea of LoRA is to introduce a pair of matrices, $A$ and $B$, to supplement $W$. $A$ and $B$ have sizes of $D_{in} \times D_{int}$ and $D_{int} \times D_{out}$, respectively, so that their multiplication, $AB$, has the same size as $W$. The intermediate dimensionality, $D_{int}$, is often set to be a small value (i.e., $D_{int} \ll \min{D_{in}, D_{out}}$), making $AB$ a low-rank matrix compared to $W$. During fine-tuning, we compute $y = W^\top x + s \cdot (AB)^\top x$, where $s$ is the coefficient for weight tuning, and $W$ is fixed while $A$ and $B$ can be adjusted, arriving at the goal of parameter-efficient fine-tuning. After fine-tuning, the computation is reformulated into $y = (W + s \cdot AB)^\top x$, where $W$ is replaced by $W’ = W + s \cdot AB$ for fast inference.
Another effective way to reduce computational costs lies in low-bit quantization. We only consider the quantization of weights throughout this paper. In particular, we apply a simple method named min-max quantization. Mathematically, given the bit width $N$ and a pre-trained weight matrix $W$, we compute the minimum and maximum values across all elements of $W$, denoted as $\min(W)$ and $\max(W)$, respectively. Then, $W$ is quantized into $\tilde{W}$ by computing
\[\tilde{W}_{i,j} = \left\lfloor \frac{W_{i,j} - \beta}{\alpha} \right\rceil\]where $\alpha = \frac{\max(W) - \min(W)}{2^N - 1}$ and $\beta = \min(W)$ are called the scaling and zero factors, respectively; $\lfloor \cdot \rceil$ denotes the integer rounding operation. All elements in $\tilde{W}$ are in the set of ${0, 1, \ldots, 2^N - 1}$ and thus stored as $B$-bit integers. The computation, $y = W^\top x$, is approximated as $y = \tilde{W}^\top x = \alpha \cdot \hat{W}^\top x + \beta x$. The quantization brings two-fold benefits, namely, the storage of $W$ is reduced (e.g., from FP16 to INT4) and the computation of $W^\top x$ becomes faster.
The cost is that $\tilde{W}$ is an approximation of $W$, which may harm the accuracy of language understanding. To reduce the quantization loss between $W$ and $\tilde{W}$, an effective strategy is to perform an individual quantization for each column of $W$. Let $W = [w_{i,j}]{D{in} \times D_{out}}$, where $i \in {1, \ldots, D_{in}}$ and $j \in {1, \ldots, D_{out}}$ are iterative variables. Let $\alpha_j$ and $\beta_j$ be the scaling and zero factors computed on the $j$-th column, $w_j$. Hence, Equation 1 is updated as $\tilde{W} = [\tilde{w}j]{D_{out}}$.
In the original (holistic) quantization, the computational cost is unchanged while the storage cost of the scaling and zero factors increases from $2$ to $2D_{out}$ floating point numbers. This is negligible compared to the reduced cost of storing the full-precision $W$.
3.2 Objective: Efficient Adaptation and Deployment
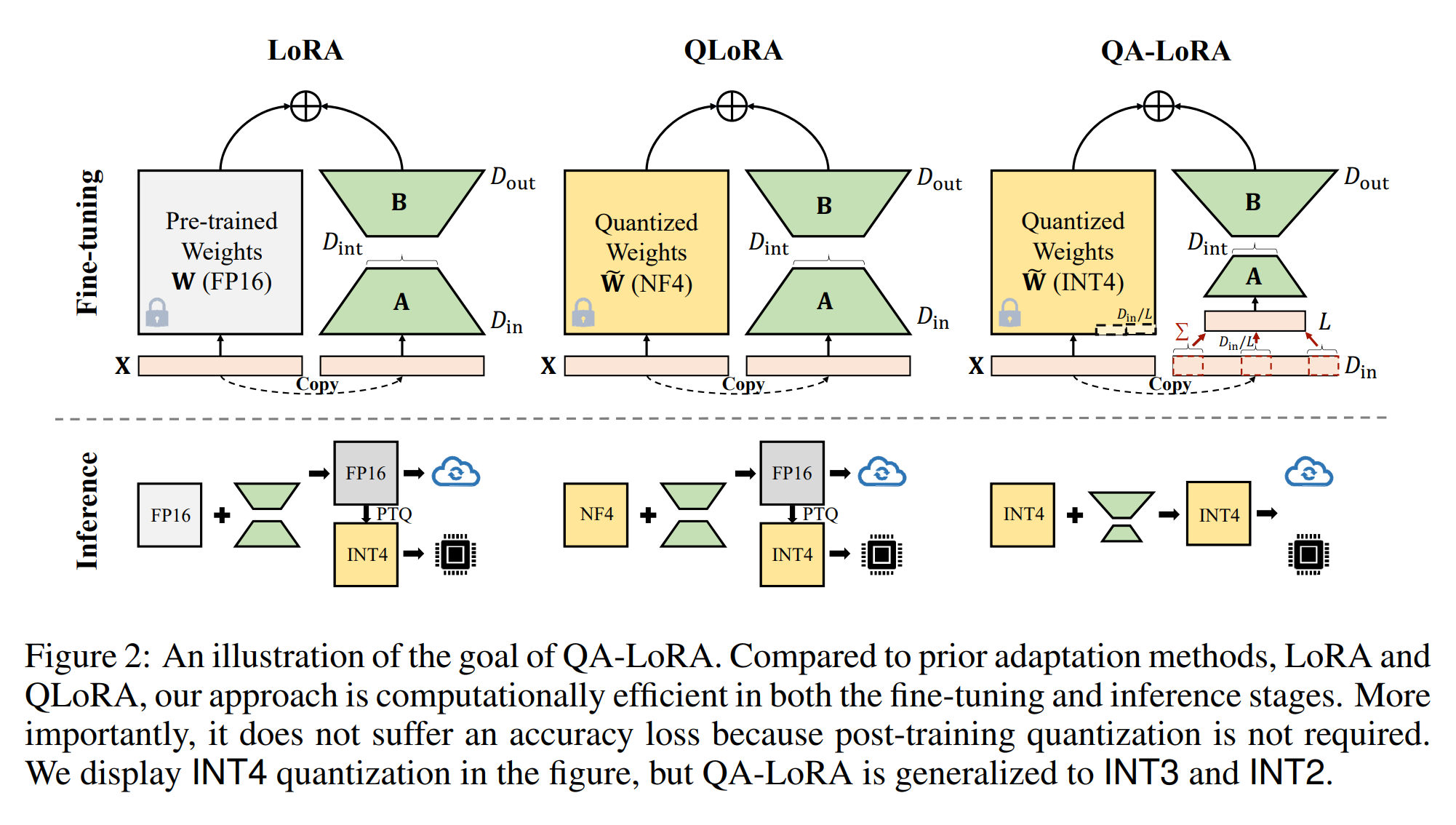
As shown in Figure 2, we aim to achieve two goals. First, during the fine-tuning stage, the pretrained weights $W$ are quantized into low-bit representation so that LLMs can be fine-tuned on as few GPUs as possible. Second, after the fine-tuning stage, the fine-tuned and merged weights $W’$ are still in a quantized form so that LLMs can be deployed with computational efficiency.
We note that QLoRA (Dettmers et al., 2023a), a recently proposed variant of LoRA, achieved the first goal. The idea is to quantize $W$ from FP16 to NF4 (a highly squeezed type of floating point numbers) during the fine-tuning stage. We learn from QLoRA that joint optimization of quantization and adaptation is tractable because the accuracy loss between $W$ and $\tilde{W}$ is compensated by the low-rank weights, $s \cdot AB$. After fine-tuning, the side weights $s \cdot AB$ must be added back to $\tilde{W}$, making the final weights $W’$ in FP16 again. Indeed, one can perform post-training quantization (PTQ) upon $W’$, but this strategy can cause a significant loss in accuracy especially when the bit width is low. Please refer to the experiments for details. Additionally, there is no operator-level optimization for NF4 yet, making it difficult to accelerate the fine-tuning and inference stages. In brief, the only benefit brought by QLoRA is the reduced memory cost for fine-tuning.
3.3 Solution: Group-Wise Quantization with Low-Rank Adaptation
From the above analysis, the key to achieving the second goal lies in that $\tilde{W}$ (i.e., the quantized $W$) and $s \cdot AB$ can be merged without using high-precision numbers (e.g., FP16). We first note that this is impossible in the original setting, i.e., $W$ is quantized into $\tilde{W}$ in a column-wise manner while both $A$ and $B$ are unconstrained.
We write down the condition using the mathematical language. Since $W’ = \tilde{W} + s \cdot AB$, we have $w’{i,j} = \tilde{w}{i,j} + s \cdot \sum_k a_{i,k}b_{k,j}$ for all $(i, j)$. Here, for any $j$, all $\tilde{w}{i,j}$ are represented using the same set of scaling and zero factors, i.e., there exist $\alpha_j$ and $\beta_j$ so that $\tilde{w}{i,j} = \alpha_j \times \hat{w}{i,j} + \beta_j$, $\hat{w}{i,j} \in {0, 1, \ldots, 2^N - 1}$. After each $\tilde{w}{i,j}$ is added by $s \cdot \sum_k a{i,k}b_{k,j}$ (abbreviated as $c_{i,j}$), if we want to keep the property for quantization, we must guarantee that for any $j$, all possible values of $c_{i,j}$ form an arithmetic set with the common difference being $\alpha_j$. This is intractable in continuous gradient-based optimization unless we ask that $c_{i,j}$ is a constant, i.e., $c_{1,j} = \ldots = c_{i,j} = \ldots = c_{D_{in},j}$ for any $j$. This is equivalent to setting all row vectors of $A$ to be the same, i.e., $a_1 \equiv \ldots \equiv a_i \equiv \ldots \equiv a_{D_{in}}$, where $\equiv$ denotes element-wise equivalence between two vectors.
The above strategy, while tractable, leads to a significant accuracy drop in practice. In particular, with all rows of $A$ being the same vector, we have $\text{rank}(A) = 1$ and thus $\text{rank}(AB) = 1$, whereas the rank of $AB$ is correlated to the ability of fine-tuning $\tilde{W}$ in new data (Hu et al., 2021; Valipour et al., 2022; Dettmers et al., 2023a). To address this issue, a straightforward idea is to relax the constraints for both quantization and adaptation.
We partition each column of $W$ into $L$ groups where, for ease of implementation, we set $L$ to be a divisor of $D_{in}$. Instead of quantizing each column of $W$ entirely, we use an individual pair of scaling and zero factors for quantization, i.e., the $l$-th group of factors, $\alpha_{l,j}$ and $\beta_{l,j}$
, are computed for $D_{in}/L$ elements in the $j$-th column. Correspondingly, we only require the row vectors of $A$ within the same group to have the same value. In our implementation, this is achieved by doing summation within each group of the input vector, $x$. This parameter-free operation reduces the dimension of $x$ from $D_{in}$ to $L$, hence we can set $A$ to be a $L \times D_{int}$ matrix without further constraints.
The proposed approach is named quantization-aware low-rank adaptation (QA-LoRA). Compared to the baselines, LoRA and QLoRA, it is implemented by inserting/modifying a few lines of code, as shown in Algorithm 1. Compared to LoRA, QA-LoRA enjoys advantages in time and memory consumption. Compared to QLoRA, QA-LoRA requires extra storage for $L \times D_{out}$ pairs of scaling and zero factors but reduces the number of parameters of $A$ from $D_{in} \times D_{int}$ to $L \times D_{int}$ – since we often set $L \ll D_{in}$, the above change is negligible. The major advantage of QA-LoRA, compared to QLoRA, lies in the inference stage where it is faster and more accurate. We compare the computational costs of LoRA, QLoRA and QA-LoRA in Table 2.
The insight of QA-LoRA: balance. QA-LoRA is very similar to a variant of QLoRA in which NF4 quantization is replaced by INT4. In this version, the number of parameters of quantization ($D_{out}$ pairs of scaling and zero factors) is much smaller than that of adaptation ($D_{in} \times D_{int} + D_{int} \times D_{out}$ parameters). This results in a significant imbalance between the degrees of freedom of quantization and adaptation. We introduce group-wise operations, increasing the number of parameters of quantization from $D_{out}$ to $L \times D_{out}$, meanwhile decreasing that of adaptation from $D_{in} \times D_{int} + D_{int} \times D_{out}$ to $L \times D_{int} + D_{int} \times D_{out}$. As we shall see in experiments, a moderate $L$ can achieve satisfying accuracy of language understanding meanwhile preserving computational efficiency.
1 The exact conditions are two-fold. For any j, there exists a new zero factor β′ that ci,j = αj × ˆci,j + β′ not greater than 2B − 1 so that the summed weights can still be quantized into B-bit integers. j and a set of integers ci,j so j. Additionally, the difference between the minimum and maximum of ˆwi,j + ˆci,j is
2 We implemented this version of QLoRA, and it reports very similar (±0.5%) accuracy compared to the original QLoRA in the few-shot experiments for MMLU.
4 EXPERIMENTS
4.1 SETTINGS
Foundation models. We establish QA-LoRA upon the LLaMA (Touvron et al., 2023a) and LLaMA2 (Touvron et al., 2023b) families. In particular, we fine-tune the 7B, 13B, 33B, and 65B models of LLaMA and the 7B and 13B models of LLaMA2.
Evaluation metrics. Following QLoRA (Dettmers et al., 2023a), we evaluate both the zero-shot and few-shot performance of the LLMs on Massively Multitask Language Understanding (MMLU) benchmark (Hendrycks et al., 2021). It consists of 57 language tasks including humanities, STEM, social science, etc. We use the official MMLU evaluation script and prompts3. We further assess the zero-shot common sense reasoning ability on tasks covering HellaSwag (Zellers et al., 2019), PIQA (Bisk et al., 2020), WinoGrande (Sakaguchi et al., 2019), ARC (Clark et al., 2018), BoolQ (Clark et al., 2019), and OpenBookQA (Mihaylov et al., 2018). We adopt lm-evalharness (Gao et al., 2021) to produce the Common Sense QA results.
Quantization. We adopt GPTQ (Frantar et al., 2023) in the quantization step, and our approach is open to other PTQ methods such as (Lin et al., 2023; Dettmers et al., 2023b). We use the same settings to quantize the QLoRA fine-tuned models and pre-trained LLaMA models. In the main experiments, we conduct a group-wise asymmetric quantization (with a group size of 32). We set the act-order variable to be false and the true-sequential variable to be true.
Datasets and training details. We choose Alpaca (Taori et al., 2023) and FLAN v2 (Longpre et al., 2023) as our fine-tuning datasets. Alpaca contains 52K instruction-following data generated from text-davinci-003 (GPT 3.5) (Wang et al., 2022). FLAN v2 is a collection of 1,836 tasks combining the mixture with CoT, Muffin, T0-SF, and NIV2. To save the tuning cost, we randomly sample a 320K subset from the FLAN v2 collection. Following QLoRA (Dettmers et al., 2023a), we use a paged AdamW optimizer, a maximum gradient norm of 0.3, and a batch size of 16 in the tuning period. We choose the constant learning rate schedule and set the learning rate to be 2 × 10−5 for the 7B and 13B models and 1 × 10−5 for the 33B and 65B models. The number of fine-tuning steps is 10K for Alpaca and 20K for FLAN v2. All experiments are conducted on Tesla V100 GPUs. We use one GPU for the 7B, 13B, and 33B models and two GPUs for the 65B models.
4.2 MAIN RESULTS AND EFFICIENCY
Comparison against recent competitors on LLaMA for MMLU. We first apply QA-LoRA to fine-tune the LLaMA models for MMLU. Table 1 summarizes the results with respect to different model sizes, fine-tuning datasets, and bit widths. Besides the base LLaMA models, we also compare QA-LoRA against QLoRA (Dettmers et al., 2023a), the most related work, and PEQA (Kim et al., 2023), a recent quantization method that does not use LoRA. We report both the original QLoRA (the inference stage involves FP16 computation) and the variant after GPTQ (for fair comparison). QA-LoRA consistently outperforms both competitors (QLoRA w/ GPTQ and PEQA) in either 0shot and 5-shot accuracy. The advantage is more significant when the model size is small (e.g., 7B and 13B) or the bit width is small (e.g., INT3 or even INT2 is used), demonstrating that QALoRA is a strong solution in the scenarios that require computational efficiency. In some cases, the INT4 version of QA-LoRA performs even better than the original version of QLoRA meanwhile the inference speed is much faster (see the next paragraph). We further demonstrate some examples of QA-LoRA in Appendix A, where one can see the qualitative comparison and QA-LoRA beyond QLoRA w/ GPTQ. QA-LoRA mainly benefits from the quantization-aware adaptation; otherwise, the post-training quantization will not be compensated, resulting in unstable results.
3 https://github.com/hendrycks/test
Table 1: 0-shot and 5-shot accuracy (%) on the Massive Multitask Language Understanding (MMLU) dataset (Hendrycks et al., 2021). Each block is based on the same foundation model specified at the first row. We organize all results using the fine-tuning dataset (Alpaca or Flan-v2) and the bit width of quantization. The bit width of ‘4 + 16’ refers to the original QLoRA where the final version for inference is in FP16.
Table 2: The numbers of learnable parameters and time costs of QLoRA and QA-LoRA during the fine-tuning stage. All results are reported on Alpaca with one Tesla-V100 GPU (the 65B model uses two chips). The number of fine-tuning steps is 10K. LLaMA-13B LLaMA-7B #Params Time(h) #Params Time(h) during the fine-tuning stage.
The significant advantage of QA-LoRA in training time mainly comes from the use of INT4 quantization. Compared to NF4 quantization used by QLoRA, INT4 operators have been optimized by CUDA and are much faster in execution. Additionally, during the inference stage, QA-LoRA is also more than 50% faster than QLoRA because the fine-tuned model (after weight integration) is still in INT4, unlike QLoRA that converts it back to FP16.
Commonsense QA results. We also evaluate QA-LoRA for 0-shot commonsense QA based on LLaMA-7B. Results are summarized in Table 3. Similar to the MMLU results, the 4-bit QA-LoRA is comparable with the mixed-precision QLoRA and outperforms the post-quantized QLoRA by an average of 2.0%. The advantage becomes more significant in low-bit scenarios, e.g., the 2-bit QA-LoRA reports a remarkable accuracy gain of 15.0% over the 2-bit post-quantized QLoRA.
On LLaMA2 models. We further validate the effectiveness of our method on LLaMA2 (Touvron et al., 2023b). As shown in Table 4, we fine-tune the 7B and 13B models of LLaMA2 and test them on MMLU. Compared to the original FP16 models, the INT4 models fine-tuned with FLAN v2 are consistently better, while those with Alpaca report slightly lower accuracy. These experiments validate that QA-LoRA is generalized to other pre-trained model families.
4.3 ABLATIVE STUDIES
Impact of the quantization group size. We investigate different settings of L, the hyper-parameter that controls the degrees of freedom for both quantization and low-rank adaptation. Results are reported in Table 5, where group size (i.e., Din/L is displayed instead of L). Recall that a larger L (corresponding to a smaller group size) implies a larger degree of freedom, i.e., a smaller quantization loss, and a larger number of adaptation parameters. Meanwhile, it also requires a larger number of storage and computation, though negligible as long as L ≫ 1. One can observe that a larger L (e.g., group size is 32) often leads to higher accuracy, and the advantage becomes more significant when the quantization bit width is small, implying that a larger quantization loss needs to be compensated by a larger degree of freedom.
Table 5: 0-shot and 5-shot MMLU accuracy (%) on with respect to different group settings.
Impact of fine-tuning datasets. We also evaluate QA-LoRA on more datasets such as Selfinstruct (Wang et al., 2022), Longform (K¨oksal et al., 2023), and Chip2 (LAION, 2023). Results are summarized in Table 6. Compared to Alpaca and FLAN v2, these datasets are relatively small, and thus the fine-tuned models report a bit weaker accuracy on MMLU. Note that, with LLaMA-13B as the foundation model, QA-LoRA consistently outperforms QLoRA with mixed precision, meanwhile being much faster in the inference stage.
Impact of the size of fine-tuning datasets. Lastly, we evaluate QA-LoRA on different subsets of FLAN v2. The dataset size varies from 160K, 240K, 320K, 400K, and 480K. LLaMA-7B is used as the foundation model. As shown in Figure 3, low-bit quantization asks for more data, yet 320K is sufficient for both the INT2 and INT4 variants of QA-LoRA.
5 CONCLUSION
Figure 3: 5-shot MMLU accuracy (%) of QA-LoRA when the LLaMA-7B model is fine-tuned on subsets of FLAN v2 with different sizes.
In this paper, we propose QA-LoRA as an efficient method that introduces quantization-awareness into the low-rank adaptation of LLMs. At the core of QA-LoRA lies the group-wise operations for both quantization and low-rank adaptation, and the key insight comes from balancing the degrees of freedom of both sides. QA-LoRA is easily implemented, generalized across various foundation models and language understanding tasks, and computationally efficient in both fine-tuning and inference stages. Extensive experiments on the LLaMA model families validate the effectiveness of QA-LoRA.